Модификации одномерных скрытых марковских моделей для задачи распознавания лиц

Гультяева Т. А., Попов А. А.
Источник: gultyaeva.sdbe.ami.nstu.ru/my_article/report8.pdf

1. ВВЕДЕНИЕ

В настоящее время наблюдается непреходящий интерес к проблеме распознавания лиц. Под распознаванием будем понимать идентификацию изображения неизвестного лица с одной из известных персон. Данная задача актуальна как в области интеллектуальных сред, так и в системах безопасности. Одни из первых разработанных методов распознавания лиц – метод главных компонент (собственных лиц), отличительной особенностью которого является то, что главные компоненты несут в себе информацию о признаках некоторого обобщенного лица. Распознавание лиц с использованием линейного дискриминантного анализа основывается на предположении о линейной разделимости классов (персон) в пространстве изображений. Нейросетевые методы обладают хорошей обобщающей способностью. Обзор этих и других методов распознавания (таких как сравнение эластичных графов, сравнение эталонов и др.) приведен в [1]. Далее мы рассмотрим распознавание лиц людей с использованием одного из статистических методов распознавания – скрытых марковских моделей (СММ) с дискретным временем [2]. Данный метод позволяет определять структурные особенности лица и учитывать характер искажений лица. Отметим, что скрытые марковские модели успешно применяются для обработки аудио сигналов, речи, изображений, распознавания текста, в биомедицине и других областях [3].

Мы остановимся на рассмотрении СММ с одномерной топологией. Несмотря на то, что этот тип моделей является простейшим, предыдущими исследователями (например, [2], [4]), как нам представляется, не до конца был раскрыт потенциал таких СММ.

2. СКРЫТЫЕ МАРКОВСКИЕ МОДЕЛИ

Далее отметим основные положения теории СММ и рассмотрим практические аспекты задачи распознавания лиц при помощи данного метода.

2.1 Элементы СММ

Элементами СММ являются:
1. Конечное множество скрытых состояний .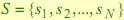
2. Конечное множество наблюдаемых состояний (или дискретный алфавит) .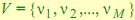
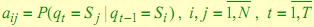3. Матрица переходных вероятностей , где ассоциируема со стационарной марковской цепью на пространстве скрытых состояний. Здесь 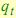со- стояние модели в момент времени t.
4. Начальная вероятность состояний , .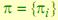
5. Матрица эмиссий 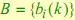, , – наблюдаемый символ в момент времени .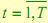
Используя полунепрерывные СММ (непрерывное пространство наблюдаемых состояний, но дискретное пространство скрытых состояний) имеем: , где – коэффициент k-ой смеси i -ого состояния, 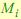– число наблюдаемых состояний, описывающих i -ое ненаблюдаемое состояние.

Начиная с [5], где впервые было предложено использовать СММ для задачи распознавания, и в дальнейших работах на эту тему [2], [4], наблюдаемые состояния выбирались во всем пространстве наблюдений и использовались M или 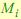элементов для описания каждого скрытого состояния. Обозначим данный метод как GB (Global Bases).

Однако для наилучшего описания 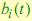мы предлагаем множество V выбирать таким образом, чтобы только 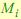конкретных наблюдаемых состояний описывали скрытое состояние (PB – Private Bases). Кроме того, эти наблюдаемые состояния выбираются из наблюдений, находящихся в этом скрытом состоянии.

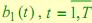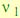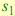Для описанных методов на рис. 1 схематично изображены наблюдаемые и скрытые состояния. Если положить , то для описания будут использоваться наблюдаемые состояния и ; при этом в методе PB описание будет происходить намного точнее, чем в GB. Если же мы будем в методе GB использовать 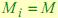, то, естественно, описание 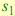будет полнее.

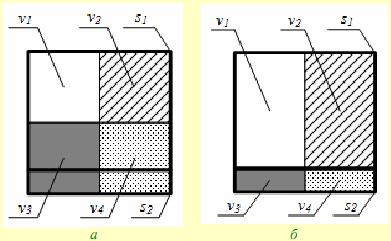
Рис. 1. Выбор наблюдаемых состояний в методе GB (а) и в методе PB (б)

При одинаковом значении числа смесей 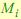метод PB позволяет повысить процент распознавания в сравнении с методом GB. Сравнивая метод PB и GB, использующий 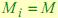, можно сделать вывод, что по качеству распознавания они практически идентичны, однако у метода PB скорость распознавания одного изображения выше. При малом значении 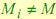метод GB недостаточно хорошо описывает обучающие данные. Предложенный же метод PB более точно настраивает СММ на воспроизведение обучающих наблюдений. В [6] мы показали, что вероятность генерации ложных наблюдений в методе PB с увеличением 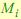снижается. При этом вероятность генерации своих тестовых наблюдений снижается. Таким образом, данный метод выбора наблюдаемых состояний приводит к высокому проценту и относительно высокой скорости распознавания.

2.2 Марковские цепи

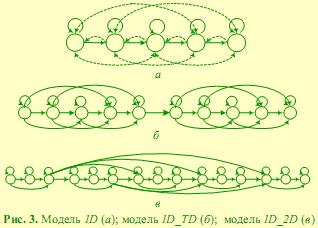
Марковские цепи, используемые в работе, имеют одномерную топологию. На рис. 3 приведены примеры марковских цепей, а также обозначения соответствующих моделей.

Условно каждое состояние ассоциируется с какой-либо частью лица. Например, состояния цепи для 1D модели можно интерпретировать как лоб, глаза, нос, губы, подбородок. Этот тип модели является простейшим, используемым для распознавания лиц [2]. Модель 1D_2D близка к псевдо-двумерным СММ, а 1D_TD (1D Two Domain) предложена нами как некий переходный вариант между 1D и 1D_2D.

Нами было установлено, что модель 1D_TD сочетает в себе достоинство 1D_2D модели – высокий процент распознавания и приемлемую скорость распознавания, присущую 1D модели [7]. На рис. 3, а наличие связей, обозначенных пунктирной линией, регулируется некоторыми дополнительными параметрами модели (см. пункт 3.2). Наличие дополнительных переходов возможно также и для моделей 1D_TD и 1D_2D.

ЗАКЛЮЧЕНИЕ

В данной статье были предложены некоторые новые методы выбора элементов СММ, влияющих на описательную способность модели (такие как, наблюдаемые состояния, марковские цепи). Рассмотрен вопрос выбора способа извлечения наблюдений и их числа.

Проведенные сравнения (например, в [9]) показали, что методы, основанные на более сложных СММ, достигают ошибки распознавания, близкой к нулю, что является наилучшим результатом среди рассмотренных методов распознавания лиц (на базе ORL). Рассмотренные нами СММ с одномерной топологией уступают по точности псевдо-двумерным и СММ, использующим иные пространства признаков. Однако, предложенные изменения в описании скрытых наблюдений и переход от 1D модели к более сложным моделям с одномерной топологией, позволили увеличить процент распознавания в среднем на 10% (сравнить с [9]).