Метод прямого обращения. Чтобы получить представление о степени неустойчивости решения обратной задачи, воспользуемся методом прямого обращения. Для этого из (4) выразим a(x)
Измерения температуры на поверхности слитка известны, поэтому поставленная задача распадается на две: определение температурного поля внутри слитка и затем уже определение коэффициента теплоотдачи a(x).
Первая задача является краевой задачей с граничными условиями 1-го рода (условия Дирихле) и 2-го рода (условия Неймана). Для её решения используется метод конечных разностей. В рассматриваемом нами прямоугольнике введём конечно-разностную сетку wq,p, равномерную по каждому направлению с шагами q, p = const, q=l/N, p=m/M, где N, M – число отрезков разбиения вдоль пространственных координат x и y соответственно (рис.2).
В результате решения конечно-разностной задачи мы получаем поле температур рассматриваемого нами участка. Чтобы вычислить производную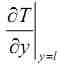 
в узлах введённой сетки, заменим её конечно-разностным аналогом.
Коэффициент теплоотдачи, найденный таким способом, мало пригоден для практического использования. Слагаемое, соответствующее лучистому теплообмену, увеличивает погрешность до четвёртого порядка. Кроме того, в формуле присутствует численное дифференцирование, которое само по себе является некорректной задачей. В конечном итоге относительно малым отклонениям (ошибкам в измерениях) температуры соответствуют достаточно большие отклонения в значениях коэффициента теплоотдачи. Результаты вычислений методом прямого обращения представлены на рис. 4.
Метод наименьших квадратов
Для применения метода наименьших квадратов примем во внимание следующую информацию.
Коэффициент a(x) имеет специальное распределение вдоль поверхности слитка. Известно, что на участке, накрываемом факелом форсунки, его можно приблизить параболической функцией, которая приобретает максимальное значение в точке, соответствующей координате сопла форсунки, а на остальных участках – константой. Так как форсунки в рассматриваемой нами секции однотипные, они дают одинаковый водо-воздушный факел, следовательно, и коэффициент теплоотдачи – одна и та же парабола, сдвинутая вдоль оси абсцисс (рис.3).
Приведём все участки под форсунками к началу координат таким образом, чтобы вершина параболы находилась над началом координат. Величина h определяется полушириной захвата факела форсунки. Следовательно, нам остаётся определить всего два параметра – А и aс. Как уже было сказано, aс = const, а на участках, подвергающихся принудительному охлаждению, будем искать a(x) в виде:
Рассмотрим сначала участки, на которых a(x) = aс = const. Обозначим множество узлов xi , в которых мы считаем КТ постоянным, К. Множество остальных узлов, где КТ распределяется согласно параболическому закону, обозначим В. Из (7) получаем формулу для невязки тепловых потоков на границе:
Обозначим
Требуется найти такое aс, чтобы сумма квадратов невязок была минимальной, т.е. чтобы выполнялось условие
Необходимое условие существования экстремума S(a):
Отсюда находим a
Каждому узлу xi из множества В поставим в соответствие точку yi на отрезке [–h, h] таким образом, чтобы |yi | равнялось расстоянию от соответствующего xi до координаты ближайшей форсунки. Из (7) и (8) получаем невязку
Найдём такое А, при котором
Из необходимого условия существования экстремума
находим А
Следует также отметить, что в определённых при помощи МНК значениях aс и А выполняется достаточное условие существования минимума функции S. Легко проверить, что частные производные второго порядка S по каждому их этих параметров строго больше нуля.
Таким образом, мы нашли сплайн-аппроксимацию распределённого в пространстве коэффициента теплоотдачи на поверхности движущегося слитка, которая даёт нам минимальное среднеквадратичное отклонение между температурой поверхности измеренной и вычисленной по модели в результате решения прямой задачи.
