ADVANCED PROCESSING OF NONUNIFORMLY SAMPLED NON-STATIONARY SIGNALS
Author: M. Greitans
Source: Electronics and Electrical Engineering. –
Kaunas: Technologija, 2005. – No. 3(59). – P. 42–45
Full version: http://www.edi.lv/dasp-web/dasp-papers/n-uniform_n-stacionary.pdf
Introduction
A signal is stationary if its statistical characteristics do not change with time. Signals of practical interest often do not comply with this requirement [1]. It has been quit difficult to satisfactorily handle non-stationary signals using conceptualizations based on stationarity, as it is assumed, for example, by classical Fourier transform. Nonstationary signals justify the need for joint time-frequency analysis and representation. Non-stationary signals may be divided into two types: momentarily transient and persistent. The momentarily transient signal has a brief, finite duration. The persistent non-stationary signal has continuous time-varying behavior. In practice the time-frequency representation is characterized by points on a time-frequency gram with a finite duration time axis and finite bandwidth frequency axis. Time-frequency analysis typically deals with signals for which the instantaneous frequency bandwidth is considerably narrower than the whole bandwidth of signal spectral characteristics [2]. As examples can be quoted chirps, Doppler signals, frequency tracking etc. To process signals digitally they should be sampled. The Nyquist criterion gives us a theoretical limit to what rate we have to periodically sample a signal that contains data at a certain maximum frequency. Once we sample below the Nyquist rate we get the spectral analysis results, which have corrupting artifacts – so called “aliases”. A dilemma concerning the choice of sampling rate arises: on the one hand the maximum signal frequency defines sampling frequency according to Nyquist, while on the other hand the narrow instantaneous bandwidth of signal at each time moment allows a considerably lower sampling density. One possible course of action in such a case is to use a nonuniform sampling technique. The proper application of nonuniform sampling suppresses the frequency aliasing and allows the use of a sampling density below the Nyquist rate [3].
It should be stated that nonuniformly taken signal samples require the focusing of more attention on the signal processing algorithm. The benefit achieved by suppression of frequency aliasing could translate into some other corrupting artifact, for example, the increased noise floor of spectrogram as it is usually for the standard spectral estimation algorithms. In this paper the advanced signal processing method will be discussed, which will provide high frequency and time resolution in a wide dynamic range of analysis.
Typical Time-frequency representations
The classical method for analyzing non-stationary signals is short time Fourier transform (STFT). It was proposed by Gabor in 1946. STFT is based on the well known Fourier transformation
 (1) (1)
From (1) follows that signal x(t) is integrated over all time. It means that one does not need to worry about time after transformation is applied. There is no attention to when the signal components of different frequencies act. The basic idea of STFT is to introduce the time window, which is moved along the signal, and in such a way time indexed spectrum can be calculated:
 (2) (2)
It is obvious from (2) that the time-frequency analysis result depends on time window g(t) choice. Long time windows provide good frequency resolution, but poor time resolution. Short time windows provide good time resolution, but poor frequency resolution [4]. STFT for signals sampled nonuniformly at time instants tk can be expressed as:
 (3) (3)
where summation involves the samples located within the selected time window with length Tg . The basic drawback of STFT is its resolution limitation. It can be improved replacing Fourier transform with high-resolution spectral estimate techniques, for example, autoregressive (AR) modeling [1, 5]. The Wigner distribution (WD) has been employed as an alternative to overcome resolution drawback of the STFT [4]. WD in general is expressed as
 (4) (4)
WD provides high-resolution representation in time and in frequency for monocomponent signals. However, if the signal consists of several subcomponents, additional interference or cross-terms appears [4, 6]. A discrete form of the WD can be expressed as
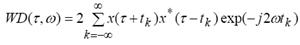 (5) (5)
Note the necessity to know signal values at
time instants 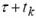 and and 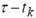 for all k
that leads to the WD application only for uniformly sampled
signals. Moreover, to avoid the distortion due to frequency aliasing,
the signal x(t) has to be sampled at twice the
Nyquist frequency for real valued signal. To overcome the disadvantages
of the cross-terms of the Wigner distribution and the resolution
limitations of the STFT, the wavelet transform (WT) is an alternative
[7]. The continuous wavelet transform of a signal x(t)
is defined as for all k
that leads to the WD application only for uniformly sampled
signals. Moreover, to avoid the distortion due to frequency aliasing,
the signal x(t) has to be sampled at twice the
Nyquist frequency for real valued signal. To overcome the disadvantages
of the cross-terms of the Wigner distribution and the resolution
limitations of the STFT, the wavelet transform (WT) is an alternative
[7]. The continuous wavelet transform of a signal x(t)
is defined as
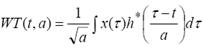 (6) (6)
where a is the scaling factor and h(t) is the so-called analyzing wavelet. The time-frequency version is obtained by making the substitution a = f0 f . The analysis can be viewed as a filter bank comprising bandpass filters with bandwidths proportional to frequency. The multiresolution nature of wavelet analysis leads to some limitations. Wavelet transform techniques use a scaling profile such that frequency resolution decreases at high frequencies, while temporal resolution decreases at low frequencies. While this choice of scaling leads to nice mathematical structures and algorithms, there is no physical reason to assume that, it is contrary to natural structure behavior. In addition, the time- and scale-sampling grid should usually be considerably oversampled, in order to get the best performance of WT analysis. This oversampling introduces redundancy in the time-scale representation.
Proposed time-frequency analysis approach
The approach developed in this paper is based on the idea of keeping the valuable features of the above mentioned classical approaches and to minimize the impact of its drawbacks. Several authors consider a promising advancement of Wigner distribution, which allows the suppression of cross-terms and the improvement of resolution. The basic idea is to obtain a signal dependent kernel instead of simple kernel selection without any reference to signal features [8]. The approach featured here is based on a signal dependent transformation [9], which is used instead of windowed exponential functions in the expression (3) for discrete STFT. In the general form the proposed transformation could be expressed as
 (7) (7)
where 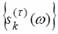 is a set
of transformation functions for time moment of analysis is a set
of transformation functions for time moment of analysis 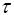 . Ts is assumed as time interval of signal’s quasi-stationarity.
From (7) it follows that the proposed transformation is applicable
to arbitrarily distributed signal samples. The signal dependent
transformation functions set is chosen in such a way that the
nature of time-frequency representation corresponds to the nature
of short time Fourier transform. In this case it is possible to
reconstruct the signal from its time-frequency representation
by inverse STFT. . Ts is assumed as time interval of signal’s quasi-stationarity.
From (7) it follows that the proposed transformation is applicable
to arbitrarily distributed signal samples. The signal dependent
transformation functions set is chosen in such a way that the
nature of time-frequency representation corresponds to the nature
of short time Fourier transform. In this case it is possible to
reconstruct the signal from its time-frequency representation
by inverse STFT.
The construction of 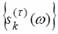 is based on
Minimum Variance (MV) filter idea to minimize variance of the
selective filter output [5, 10]. The frequency response of such
a filter adapts to the input signal on each frequency of interest.
The variance of the output is is based on
Minimum Variance (MV) filter idea to minimize variance of the
selective filter output [5, 10]. The frequency response of such
a filter adapts to the input signal on each frequency of interest.
The variance of the output is 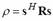 , where s is vector of filter coefficients
and R is signal autocorrelation matrix. To guarantee
that sinusoid with frequency w0 passes through the filter designed
for this frequency , where s is vector of filter coefficients
and R is signal autocorrelation matrix. To guarantee
that sinusoid with frequency w0 passes through the filter designed
for this frequency 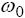 without distortion the following condition
have to be considered without distortion the following condition
have to be considered
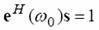 (8) (8)
where . The coefficients s under condition (8)
can be calculated as . The coefficients s under condition (8)
can be calculated as
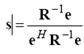 (9) (9)
To obtain the whole time-frequency representation
of the signal the calculation of coefficient vector (9) should
be performed for each grid point  of time-frequency representation. of time-frequency representation.
References
1. Akay M. (editor). Time frequency and wavelets in biomedical signal processing // IEEE Press, 1998.
2. Brueller N.N., Peterfreund N., Porat M. Non-stationary signals: optimal sampling and instantaneous bandwidth estimation. // Proc. of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis, Pittsburgh, USA, 6-9 Oct 1998. – P.113-115.
3. Bilinskis I., Mikelsons A. Randomized Signal Processing // Prentice-Hall, 1992.
4. Hlawatsch F., Boudreaux-Bartels G.F. Linear and quadratic time-frequency signal representations // IEEE Signal Proc. Mag., vol 9, April 1992. – P. 21-67
5. Marple S.M. Digital spectral analysis with applications // Prentice-Hall, 1987.
6. Cohen L. Time-Frequency Distributions-A review // Proc. IEEE, vol 77, no. 7, 1989. – P. 941-980.
7. Chui C. K. Wavelet Analysis and its Applications // Boston, MA: Academic Press, 1992.
8. Baraniuk R.G., Jones D.L. A signal-dependent timefrequency representation: Optimal kernel design // IEEE Trans.Signal Proc., vol41, no. 4, April 1993. – P.1589-1602
9. Greitans M. Enhanced signal processing in time and frequency domains in the case of non-uniform sampling // International Conference on Sampling Theory and Application SampTA'03, May 26-29, 2003, Strobl, Salzburg, Austria. – P. 35-37.
10. Greitans M. Multiband signal processing by using nonuniform sampling and iterative updating of autocorrelation matrix // Proc. of the 2001 International Conference on Sampling Theory and Application, May 13- 17, 2001, Orlando, Florida, USA. – P.85-89.
11.Greitans M. Iterative reconstruction of lost samples using updating of autocorrelation matrix // Proc. of the International Workshop "SampTA'97”, Aveiro, Portugal, 1997. – P.155- 160
|

