УСОВЕРШЕНСТВОВАННАЯ ОБРАБОТКА НЕРАВНОМЕРНО ДИСКРЕТИЗИРОВАННЫХ НЕСТАЦИОНАРНЫХ СИГНАЛОВ.
Автор: М.Грейтанс
Источник: Электроника и электротехника. – Каунас:
Технология, 2005. – №3(59). – с.42–45.
Перевод: Орленко А.Н.
Оригинальная статья: http://www.edi.lv/dasp-web/dasp-papers/n-uniform_n-stacionary.pdf
Вступление
Сигнал называется стационарным, если его статистические характеристики не меняются со временем. На практике сигналы часто не соответствуют этому требованию. Достаточно тяжело удовлетворительно обрабатывать нестационарные сигналы, используя концепции, предполагающие его стационарность, как например, классическое преобразование Фурье. Нестационарные сигналы обосновывают необходимость совместного частотно-временного анализа и представления.
Нестационарные сигналы можно разделить на 2 типа: моментно-переходные и устойчивые. Моментно-переходные имеют короткую, конечную продолжительность. Устойчивые нестационарные сигналы имеют длительное, изменяющееся во времени поведение. На практике частотно-временное представление характеризуется точками на частотно-временной диаграмме с конечными временной и частотной осями.
На практике частотно-временной анализ применяется к сигналам, у которых мгновенная полоса значительно уже, чем вся полоса спектральных характеристик сигнала. В качестве примера можно привести сигналы с линейно изменяющейся частотой, сигналы Доплера, сигналы следящей частотф и т.д. Для цифровой обработки сигнала его необходимо дискретизировать. Критерий Найквиста дает нам теоретический предел для скорости, с которой необходимо периодически дискретизировать сигнал, содержащий данные на конкретной максимальной частоте. Как только мы дискретизируем сигнал с частотой меньшей, чем частота по критерию Найквиста, мы получим результаты анализа, которые содержат искажающие артефакты. Возникает проблема выбора частоты дискретизации: с одной стороны максимальная частота сигнала определяет необходимость дискретизации сигнала в соответствии с критерием Найквиста, в то время как с другой стороны узкая мгновенная полоса сигнала позволяет использовать значительно более низкую плотность дискретизации. Один из возможных вариантов действия в этом случае – использование неравномерной дискретизации. Правильное применение неравномерной дискретизации подавляет частотный элайзинг и позволяет использование плотности дискретизации меньшей, чем по критерию Найквиста.
Необходимо сказать, что неравномерно взятые отчеты требуют фокусирования большего внимания на алгоритме обработки сигналов. Выгода, достигаемая за счет подавления частотного элайзинга может вылиться в некоторые другие искажающие артефакты, например повышенный уровень шумов, если использовать стандартные алгоритмы оценки спектра. В этом документе будет обсуждаться усовершенствованный метод обработки сигналов, который дает высокое разрешение по частоте и по времени в широком динамическом диапазоне.
Классические частотно-временные представления.
Классический метод для анализа нестационарных сигналов – кратковременное преобразование Фурье. Было предложено Габором в 1946м году. КПФ базируется на хорошо известном классическом преобразовании Фурье
 (1) (1)
Из выражения (1) следует, что сигнал интегрируется на бесконечном временном интервале. Это означает, что не нужно беспокоиться о времени при использовании этого преобразования. Не уделяется вниманию тому, когда имеют место те или иные частотные компоненты сигнала. Базовая идея КПФ состоит во введении временного окна, которое двигается вдоль сигнала. В таком случае можно вычислить спектр, индексированный во времени.
 (2) (2)
Из выражения (2) очевидно, что результаты частотно-временного
анализа зависят от выбора временного окна g(т). Длинные окна дают
высокое разрешение по частоте, но скудное по времени. Короткие
окна обеспечивают высокое разрешение по времени, но низкое по
частоте. КПФ для неравномерно дискретизированых сигналов в моменты
tk может быть выражено
 (3) (3)
Где суммирование включает все отчеты, расположенные внутри выбранного временного окна с длиной Tg. Основной недостаток КПФ – его ограничения по разрешению. Его можно улучшить, заменив КПФ другой более высокоразрешающей техникой оценки спектра, например авторегрессивным моделированием.
Распределение Вигнера использовалось как альтернатива КПФ, чтобы преодолеть его недостатки по разрешению. В общем случае распределение Вигнера выражается так:
 (4) (4)
Распределение Вигнера обеспечивает высокое разрешение по частоте и по времени для монокомпонентных сигналов. Однако, если сигнал состоит из нескольких компонент, появляется дополнительная интерференция или кросс-компоненты.
В дискретной форме распределение Вигнера выражается так:
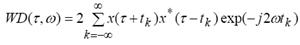 (5) (5)
Заметьте необходимость знать значения сигнала в моменты 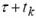 и и 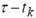 что приводит к возможности применения распределения Вигнера только для равномерно дискретизированых сигналов. Более того, чтобы избежать искажений из-за частотного элайзинга, сигнал должен быть дискретизирован с частотой вдвое больше, чем по критерию Найквиста для вещественного сигнала. что приводит к возможности применения распределения Вигнера только для равномерно дискретизированых сигналов. Более того, чтобы избежать искажений из-за частотного элайзинга, сигнал должен быть дискретизирован с частотой вдвое больше, чем по критерию Найквиста для вещественного сигнала.
Чтобы преодолеть недостатки кросс-компонент в распределили Вигнера и ограничения по разрешению КПФ, может быть использовано вейвлет преобразование. Текущее вейвлет преобразование для сигнала х(т) определяется как
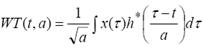 (6) (6)
Где a – это масштабирующий фактор и
h(t) так называемый анализирующий вейвлет. Частотно-временную
версию можно получить, произведя замену a=f0/f
Анализ можно рассматривать как набор фильтров, содержащий полосовые
фильтры с полосой пропускания пропорциональной частоте. Многомасштабная
природа вейвлет анализа ведет к некоторым ограничениям. Техники
Вейвлет преобразования используют такой масштабирующий профиль,
что разрешение по частоте снижается на высоких частотах, а временное
разрешение – на низких. Хотя такой выбор масштабирования приводит
к замечательным математическим структурам и алгоритмам, нет физических
причин полагать, что оно противоположно натуральному поведению
структуры.
Предлагаемый подход частотно-временного анализа
Подход, разработанный в этой статье, базируется на идее сохранения ценных свойств выше упомянутых классических подходов и минимизации их недостатков. Несколько авторов проабатывают многообещающее улучшение распределения Вигнера, которое позволяет подавить кросс-компоненты и улучшить разрешение. Базовая идея состоит в получении ядра, которое зависти от сигнала вместо того, чтобы просто выбирать ядро никак не связанное со свойствами сигнала. Подход, рассматриваемый здесь, базируется на преобразовании, зависящем от сигнала, которое используется вместо экспоненциальных функций, заключенных в окно в выражении (3) для дискретного КПФ. В общей форме предлагаемое распределение может быть выражено так
 (7) (7)
где 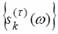 – набор функций преобразования на момент – набор функций преобразования на момент 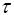 . Tsпредполагается как интервал, на котором сигнал квазистационарен. Из (7) следует, что предлагаемое преобразование применимо для произвольно распределенных отчетов. Сигналозависимый набор функций преобразования выбирается таким образом, чтобы природа частотно-временного представления соответствовала природе КПФ. В таком случае возможным будет восстановление сигнала из частотно-временного представления обратным КПФ . Tsпредполагается как интервал, на котором сигнал квазистационарен. Из (7) следует, что предлагаемое преобразование применимо для произвольно распределенных отчетов. Сигналозависимый набор функций преобразования выбирается таким образом, чтобы природа частотно-временного представления соответствовала природе КПФ. В таком случае возможным будет восстановление сигнала из частотно-временного представления обратным КПФ
Построение набора 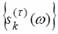 базируется на фильтре минимальной дисперсии, чтобы минимизировать отличие сигнала на выходе селективного фильтра. Частотная характеристика такого фильтра адаптируется ко входному сигналу на каждой интересующей частоте. Отличие сигнала на выходе определяется базируется на фильтре минимальной дисперсии, чтобы минимизировать отличие сигнала на выходе селективного фильтра. Частотная характеристика такого фильтра адаптируется ко входному сигналу на каждой интересующей частоте. Отличие сигнала на выходе определяется 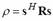 , где s – вектор коэффициентов фильтра и R – автокорреляционная матрица сигнала. Чтобы гарантировать, что синусоида с частотой , где s – вектор коэффициентов фильтра и R – автокорреляционная матрица сигнала. Чтобы гарантировать, что синусоида с частотой 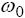 пройдет через фильтр, спроектированный для данной частоты, без искажений, необходимо, чтобы выполнялось следующее условие: пройдет через фильтр, спроектированный для данной частоты, без искажений, необходимо, чтобы выполнялось следующее условие:
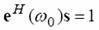 (8) (8)
где  . Коэффициенты s из условия (8) можно рассчитать как: . Коэффициенты s из условия (8) можно рассчитать как:
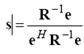 (9) (9)
Чтобы получить полное частотно-временное представление
сигнала, необходимо провести вычисление вектора коэффициентов
(9) для каждой точки  на частотно-временной диаграмме. на частотно-временной диаграмме.
|

