ОБРАБОТКА МНОГОПОЛОСНЫХ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ НЕРАВНОМЕРНОЙ ДИСКРЕТИЗАЦИИ И ИТЕРАТИВНОГО ОБНОВЛЕНИЯ АВТОКОРРЕЛЯЦИОННОЙ МАТРИЦЫ
Автор: М. Грейтанс
Источник: Proceedings of the 2001 International Conference on Sampling Theory and Application, 13-17 Мая, 2001, Орландо, Флорида, США, с. 85-89
Перевод: Орленко А.Н.
Оригинальная статья: http://www.edi.lv/dasp-web/dasp-papers/Greitans_sampta01.pdf
Краткий обзор
Рассматривается подход по обработке многополосного сигнала. Метод, обсуждаемый в данной статье, базируется на неравномерной дискретизации, фильтре минимальной дисперсии и итеративном обновлении автокорреляционной матрицы сигнала. Это позволяет обрабатывать многополосный сигнал даже, если число известных отсчетов сигнала меньше, чем по критерию Найквиста для равномерно дискретизированных сигналов. Предлагаемый подход по обработке многополосных сигналов подходит для спектрального анализа, оценки спектральной плотности мощности, автокорреляционных функций, а также для восстановления сигнала. Информация о граничных частотах полос сигнала дает возможность восстановить сигнал в отдельных полосах. Это означает, что предлагаемый метод предоставляет также возможность по фильтрации отдельных полос. Работа метода демонстрируется на примере обработки совместного сигнала GSM900 и GSM1800.
1. Введение
Часто многополосная обработка сигналов базируется на расчете специальных последовательностей отсчетов в соответствии с расположением сигнала в спектральной области. Возможность по достижению минимальной плотности отсчетов (эквивалент скорости Найквиста для равномерной дискретизации) зависит от возможности покрыть частотную область группой преобразований. В общем случае рассчитанные моменты отсчетов многополосного сигнала распределены неравномерно, поэтому любые изменения в границах субполос сигнала ведут к необходимости перерасчета последовательностей отсчетов.
В статье обсуждается обработка многополосных сигналов в случае, если используется случайная неравномерная дискретизация. Если она обладает свойством подавлять частотную утечку энергии, то не предъявляется специальных требований к точным значениям моментов дискретизации. Только два общих условия должны рассматриваться: интервал между двумя известными отсчетами и плотность отсчетов должны соответствовать эквивалентной полосе сигнала [3,4] .
Традиционно методы обработки сигналов учитывают только один параметр – спектральную плотность мощности сигнала, то есть частотные границы сигнала. Если такие границы существуют, то сигналы называются сигналами с ограниченной полосой. Функция спектральной плотности мощности многополосного сигнала состоит из нескольких отдельных частотных регионов. И она может проявляться по-разному в этих спектральных субполосах. Один из способов охарактеризовать форму спектральной плотности мощности – использование эквивалентной полосы сигнала с ограниченной полосой, определяемой по выражению
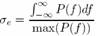 (1) (1)
Очевидно, что в реальном применении значение эквивалентной полосы меньше, чем действительная полоса сигнала. Поэтому, как показано в [4], неравномерная дискретизация позволяет обрабатывать сигналы, используя меньше отсчетов, чем по критерию Найквиста для обшей ширины полосы сигнала.
2. Метод обработки
Наличие нескольких субполос в многополосном сигнале определяет необходимость разработки специального метода обработки, который учитывает информацию о границах частотных регионов сигнала. Предлагаемый подход по обработке многополосных сигналов базируется на фильтре минимальной дисперсии [3, 5]. Базовая идея состоит в минимизации дисперсии выходного сигнала узкополосного фильтра. Частотная характеристика такого фильтра адаптируется ко входному сигналу на каждой интересующей частоте. Дисперсия выходного сигнала определяется как:
 (2) (2)
где а – вектор коэффициентов фильтра, R – автокорреляционная матрица сигнала. В дополнение коэффициенты фильтра должны гарантировать, что частоте f0 усиление частотной характеристики фильтра равно 1. Это требование может быть описано так:
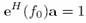 (3) (3)
где  . С другой стороны, выражение (3) означает, что синусоида с частотой f0 проходит через фильтр, разработанный для данной частоты без искажений. В [6] показано, что коэффициенты фильтра по условию (3) для частоты f0 рассчитываются так: . С другой стороны, выражение (3) означает, что синусоида с частотой f0 проходит через фильтр, разработанный для данной частоты без искажений. В [6] показано, что коэффициенты фильтра по условию (3) для частоты f0 рассчитываются так:
 (4) (4)
Учитывая выражение (3), выходной сигнал S, определяемый по выражению:
 , (5) , (5)
может интерпретироваться как комплексная спектральная величина (аналогично преобразованию Фурье) сигнала x на частоте f0 [7.] Поэтому спектральная плотность мощности сигнала на этой частоте может быть рассчитана:
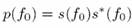 (6) (6)
Для задачи обработки многополосного сигнала каждая субполоса такого сигнала должна быть покрыта набором таких фильтров. Расстояние между частотами фильтров может быть выбрано равным частотному шагу дискретного преобразования Фурье.
Согласно выражению (4), коэффициенты фильтра зависят от автокорреляционной матрицы сигнала. Обычно значения этой матрицы заранее неизвестны. Поэтому оценки этой матрицы должны быть рассчитаны из известных отсчетов сигналов. Традиционный подход для получения корреляционной матицы базируется на усреднении взаимных произведений отсчетов сигнала. Но он не применим в случае неравномерной дискретизации, поскольку интервалы между точками дискретизации распределены неравномерно. Вместо этого для расчета R используются взаимоотношения автокорреляционных функций и функций спектральной плотности мощности сигнала:
 (7) (7)
Более того, выражение (7) позволяет учесть известные значения субполос сигнала, поскольку интегрирование необходимо производить только в определенных частотных диапазонах. Самый простой способ получить оценку спектральной плотности мощности из отсчетов сигнала в случае неравномерной дискретизации – использовать дискретное преобразование Фурье. В соответствии с подходом, описанным выше, спектральный анализ производится на фиксированном наборе частот f = [f1; f2; :::fM]. Известные значения сигнала x = [x1; x2; :::xN] выбраны в известные моменты t = [t1; t2; :::tN]. Таким образом, значения автокорреляционной функции можно получить так:
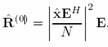 (8) (8)
где 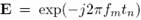 . Значения автокорреляционной
матрицы сигнала, полученные по выражению (8), это скорее грубая
оценка, которая ведет и к грубой оценке значений комплексной спектральной
функции сигнала. . Значения автокорреляционной
матрицы сигнала, полученные по выражению (8), это скорее грубая
оценка, которая ведет и к грубой оценке значений комплексной спектральной
функции сигнала.
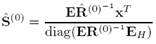 (9) (9)
и спектральной плотности мощности
 (10) (10)
Специальный итеративный алгоритм обновления, аналогичный описанному в [4,7], используется для улучшения результатов обработки. Согласно этому алгоритму оценка автокорреляционной матрицы (i+1)-го порядка получается из оценки i-го порядка следующим образом:
 (11) (11)
Теперь, используя матрицу 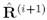 , оценка , оценка 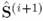 и и 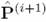 может быть получена из выражений (9)-(10). В сущности, был получен итеративный алгоритм. Итеративный процесс может быть остановлен, когда разность может быть получена из выражений (9)-(10). В сущности, был получен итеративный алгоритм. Итеративный процесс может быть остановлен, когда разность 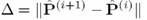 будет достаточно малой. будет достаточно малой.
Хотя матрица  симметричная и содержит только положительно определенные значения, она становится грубо определенной, с увеличением известных отсчетов [9]. В этом случае прямая инверсия этой матрицы приводит к ошибкам обработки. Поэтому выражения для получения спектральной плотности мощности сигнала может быть выведено как: симметричная и содержит только положительно определенные значения, она становится грубо определенной, с увеличением известных отсчетов [9]. В этом случае прямая инверсия этой матрицы приводит к ошибкам обработки. Поэтому выражения для получения спектральной плотности мощности сигнала может быть выведено как:
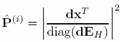 (12) (12)
где матрица d является решением следующего уравнения:
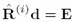 (13) (13)
Выражение (13) может быть решено итеративными методами [9,10]. Как упоминалось выше, вектор S можно интерпретировать как комплексную спектральную величину, поэтому обратное дискретное преобразование Фурье может быть использовано для получения значений восстанавливаемого сигнала [7]. Если задача по обработке многополосного сигнала состоит в фильтрации субполос, то для обратного ДПФ можно использовать только определенные конкретные части значений вектора S.
|

