| ДонНТУ | Портал магистров ДонНТУ | Главная | Реферат | Ссылки | Отчет о поиске | Индивидуальное задание |
Назад в Библиотеку
4.2 Correlation-based Techniques
D. Maltoni, D. Maio, A. K. Jain, S. Prabhakar
Источник: http://bias.csr.unibo.it/maltoni/handbook/
Перевод с английского языка Петровой Т. В.
4.2 Метод сопоставления отпечатков пальцев, основанный на корреляцииD. Maltoni, D. Maio, A. K. Jain, S. Prabhakar.Выдержки из раздела 4 "Сопоставление отпечатков пальцев" из книги «Handbook of fingerprint recognition».Суть метода заключается в следующем. Полученный со сканера отпечаток пальца накладывается на каждый эталон из базы данных поочередно, после чего прямо по пикселям изображений осуществляется просчет различий между ними. Правда, при этом приходится учитывать один момент. Дело в том, что человек каждый раз прикладывает палец под разными углами и не точно в одно и то же место рабочей области сканера. А это значит, что процесс сравнения отпечатка его пальца с эталонами должен включать в себя множество итераций, на каждой из которых изображение, полученное со сканера, поворачивается под небольшим углом или чуть-чуть смещается. Таким образом, подсчитывается корреляция (по уровню интенсивности) между соответствующими пикселями, вычисленная для различных выравниваний изображений друг относительно друга (например, путем различных смещений и вращений); по соответствующему коэффициенту принимается решение об идентичности отпечатков. Пусть T и I два изображения отпечатка пальца, соответствующие шаблонному и введенному изображениям соответственно. Тогда их разница- это сумма квадрата разности (SSD) между значениями яркости соответствующих пикселей. SSD(T,I) = ||T-I||2 = (T-I)T*(T-I) = ||T||2 + ||I||2 - 2*TT*I (1) где надстрочный индекс Т означает транспонирование вектора. Если термы ||T||2 и ||I||2 являются константами, то разница между двумя изображениями минимизируется, когда взаимная корреляция (СС) максимизируется: CC(T,I)= TT*I (2)
CC(T,I) появляется как третий терм в уравнении 1. Взаимная корреляция (простая корреляция) – мера сходства изображений. Вследствие перемещения и ротации, которые неизбежно характеризуют два различных изображения отпечатка с одного пальца, их сходство не может быть легко вычислено путем наложения изображений T и I друг на друга и применением уравненя 2. Пусть I( S(T,I) = max Непосредственное применение уравнения 3 редко приводит к приемлемым результатам по нижеприведенным причинам: 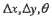 ) требует 16000 операций умножения и 16000 операций суммирования (при игнорировании граничного эффекта).Если оба значения ) требует 16000 операций умножения и 16000 операций суммирования (при игнорировании граничного эффекта).Если оба значения 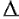 x, x, 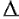 y будут изменятся с шагом в 1 пиксель в пределах диапазона [-200;200] и y будут изменятся с шагом в 1 пиксель в пределах диапазона [-200;200] и  - с шагом в 10 в пределах диапазона [-300;300] мы должны будем вычислить 401х401х61 взаимных корреляций, что составляет примерно 1569 биллионов операций умножения и операций суммирования (боле одного часа вычислений на компьютере, выполняющем 500 MIPS (миллионов команд в секунду)). - с шагом в 10 в пределах диапазона [-300;300] мы должны будем вычислить 401х401х61 взаимных корреляций, что составляет примерно 1569 биллионов операций умножения и операций суммирования (боле одного часа вычислений на компьютере, выполняющем 500 MIPS (миллионов команд в секунду)).С целью упрощения вычислительной сложности корреляционной техники применяются интеллектуальные подходы для достижения эффективной реализации. Корреляционная теорема (Gonzales , Woods, 1992) гласит, что вычисление корреляции в пространственной области (оператор T где F(.) - преобразование Фурье вышеуказанного изображения; "*" - комплексное сопряжение; "x" - поточечное умножение двух векторов. Результатом уравнения 4 является корреляционное изображение, зачение которого в пикселе [x,y] соответствует корреляции между T и I, когда смещение |
![]()
ВВЕРХ
| ДонНТУ | Портал магистров ДонНТУ | Главная | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание |
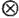 ) эквивалент выполнения поточечного умножения в распределении Фурье, в частности:
) эквивалент выполнения поточечного умножения в распределении Фурье, в частности: