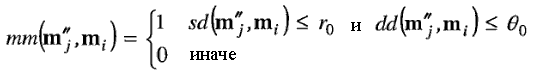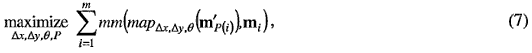| ДонНТУ | Портал магистров ДонНТУ | Главная | Реферат | Ссылки | Отчет о поиске | Индивидуальное задание |
Назад в Библиотеку
4.3 Minutiae-based Methods
D. Maltoni, D. Maio, A. K. Jain, S. Prabhakar
Источник: http://bias.csr.unibo.it/maltoni/handbook/
Перевод с английского языка Петровой Т. В.
4.3 Методы сопоставления отпечатков пальцев, основанные на извлечении деталейD. Maltoni, D. Maio, A. K. Jain, S. Prabhakar.Выдержки из раздела 4 "Сопоставление отпечатков пальцев" из книги «Handbook of fingerprint recognition».Методы, основанные на извлечении деталей являются несомненно наиболее известными и широко-применимыми методами для сопоставления изображений отпечатков пальцев, благодаря их строгой аналогии с методами судебной экспертизы сравнения отпечатков пальцев и подтверждению их действенности и эффективности при проведении судебных дел во многих странах. Постановка задачи Пусть T и I представляют собой шаблонное и введенное изображения отпечатка пальца, соответственно. В отличие от методов, базирующихся на корреляции, где представление отпечатка пальца совпадает с изображением отпечатка пальца, здесь представление – это вектор признаков (переменной длины), элементами которого являются детали отпечатка пальца. Каждая деталь описывается некоторым количеством атрибутов, включая ее размещение на изображении отпечатка пальца, ориентацию, тип (например, окончание выступа или раздвоение выступа), вес, зависящий от качества изображения отпечатка пальца в соседстве от детали, и многим другим. Наиболее распространенные алгоритмы поиска соответствия, основанные на деталях, рассматривают каждую деталь как тройственный вектор m={x, y, T = {m1, m2,...,mm}, mi = {xi, yi, I = {m1', m2',...,mn'}, mj' = {xj', yj', где и означают количество деталей в изображениях T и I, соответственно. Деталь mj' в I и деталь mi в Т полагают «соответствие», если пространственное расстояние (sd) между ними меньше допустимого ro и разница в направлении (dd) между ними меньше допустимого угла
В уравнение 6 используется вычисление минимума из | Совмещение (выравнивание) двух отпечатков пальцев – это обязательный шаг необходимый для того, чтобы максимизировать количество сопоставимых (согласующихся) деталей. Корректное совмещение двух отпечатков пальцев безусловно требует перемещения (в направлениях х и у) и ротации ( Пусть map(.) - это функция отображения детали mj' (из I) в mj" в соответствии с исходным геометрическим преобразованием. Например, принимая во внимание смещение [
Пусть mm(.) - это индикационная функция, которая возвращает 1 в случае, если детали mj" и mi сопоставимы согласно уравнениям 5 и 6.
Тогда проблема поиска соответствия может быть сформулирована, как:
где P(i) - неизвестная функция, которая определяет сочетание в пару деталей (соответствие между соответствующими деталями) в изображениях I и T; в частности, каждая деталь может иметь в точности только одну парную ей деталь на другом изображении отпечатка пальца или не иметь ни одной парной детали вообще:
Обозначим, что, в общем,P(i) = j не обязательно означает, что детали mj' и mi сочетаются в пару согласно с уравнениями 5 и 6, но только если они наиболее вероятная пара при текущем преобразовании. Уравнение 7 требует, чтобы количество парных деталей было максимизировано, независимо от того, насколько точно устанавливается это соответствие. Другими словами, если две детали удовлетворяют уравнениям 5 и 6, тогда их вклад в уравнение 7 производится независимо от их пространственного расстояния и разницы в их направлении. Альтернативы уравнению 7 могут быть представлены, когда разность (пространственное расстояние и разница в направлении деталей) для оптимального совмещения пар деталей также принимается во внимание. Решение проблемы сопоставления деталей является тривиальным (очевидным), когда известно корректное расположение ( 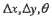 (mj') близко к mi среди деталей (mj') близко к mi среди деталей
{mk" = map 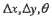 (mk') | k = 1..n, mm(mk",mi) = 1}; (mk') | k = 1..n, mm(mk",mi) = 1};
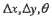 (mk',mi) = 0. (mk',mi) = 0.
Выполняя все 4 ограничения, каждая сопряженная (сочтенная в пару) деталь mj" должна быть помечена с целью избежать ее сопряжения в пару дважды и более. Рисунок 4.4 показывает пример сопряжения деталей, полученный при сопоставлении изображений отпечатков пальцев.
Рисунок 4.4 – Детали из I отображаются (наносятся на карту) в координаты Т для данного выравнивания. Детали из Т обозначаются стрелкой с началом о, в то время как детали из I – стрелкой с началом х. Отметим, что детали I относятся к m", так как они отобразились в Т координаты (что показано на рисунке). Сочетание в пару выполняется согласно критерию минимальное расстояние. Пунктирные окружности указывают максимальное пространственное расстояние. Серые окружности означают успешно сопоставленные детали; деталь m1 из Т и деталь m3" из I не имеют парных, детали m3 и m6" не могут быть сопоставлены в пару в связи с их огромной разницей в направлении. Для достижения оптимального сопряжения (согласно уравнению 7), должна быть принята незначительно более усложненная схема: фактически, в случае, если деталь из выходит за пределы пространства допусков или более чем одной детали в Т, оптимум достигается, когда максимизируется количество сопоставившихся пар (простой пример представлен на рисунке 4.5).
Рисунок 4.5 – В этом примере, если m1 будет сопоставлена с m2" (наиболее точно соответствующая (ближайшая) деталь), m2 останется без пары; однако сочетание в пару m1 с m1" приведет к тому, что деталь m2 будет сопоставлена с m2" таким образом максимизируя выражение 7. В литературе распознавания образов проблема распознавания деталей, как правило, адресуется как проблема сопоставления точечных образов. Центральную роль во многих задачах распознавания образов и компьютерного зрения занимает сопоставление точечных образов, которым в значительной степени занимаются приводящие к хорошим результатам семейства аппроксимации, известные как релаксационные методы, алгебраические и ориентационные исследовательские решения, методы минимизации энергии, методы, основанные на преобразовании Hough и др. |
![]()
ВВЕРХ
| ДонНТУ | Портал магистров ДонНТУ | Главная | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание |
 }, который указывает координаты х и у расположения детали и угол детали
}, который указывает координаты х и у расположения детали и угол детали 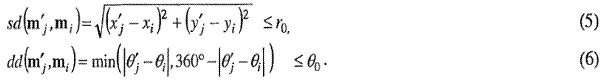
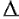 x,
x,