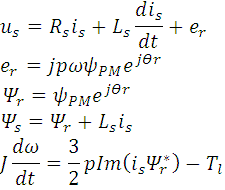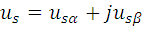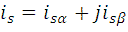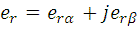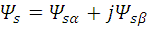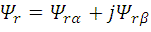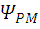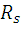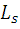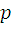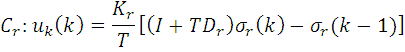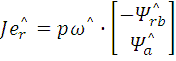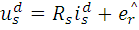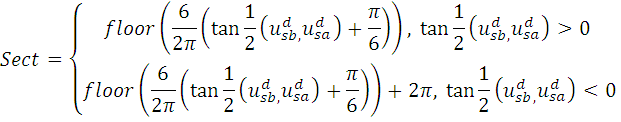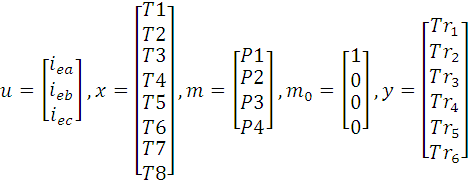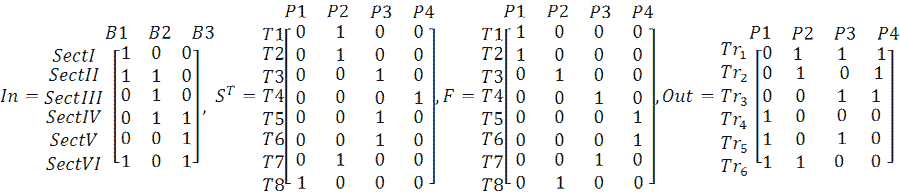Speed Sensorless Control of PM synchronous machine using Direct Current Control

Evgen Urlep, Ales Polic and Karel Jezernik

Faculty of Electrical Engineering and Computer Science, University of Maribor

Keywords

      Sensorless control, Permanent magnet motor, Sliding mode control, Direct current control, Discrete Event systems, Petri nets

Abstract

      In this paper a novel algorithm for torque and speed sensorless PMSM control is described. The PMSM rotor position and speed is acquired using sliding-mode rotor flux observer. Observer is based on the model of the PMSM where the derivation of the estimated stator flux is calculated from measured stator voltage and current. When implementing a multiple-loop control of a drive on a single processor, most of the computational time is devoted to the inner current-control loop calculation and generation of output voltage vectors in order to obtain proper drive current signal. The speed of the current controller and modulator is therefore essential for the performance of the control. Major attention is paid to current control constructed as Direct Current Control using event-driven approach and implemented on FPGA. Event-driving determines the transistor switching pattern directly from the current error logic signals change and is designed using a novel matrix based description of the discrete event systems. It is based on matrix description of Petri Nets, supplemented with a combination of logic and algebraic equations and introduces a kind of state-space description for discrete event systems. The control algorithms designed by proposed approach can be easily implemented on modern FPGA devices, which enable parallel execution of the calculations, comparing to the traditional sequential executions on the DSPs. Instead of traditional coding, the control algorithms are loaded in the form of logical matrices. The approach is utilized for torque/speed control based on the sliding mode rotor flux observer. The results of computer simulations are presented as well as the experimental hardware setup.

Introduction

      Permanent magnet synchronous motors (PMSM) are attractive candidates for speed sensorless drives as electric vehicles, pumps, compressors, etc. To control PMSMs, information about rotor position and speed is necessary. Therefore, position and speed sensorless control has been desired and several methods have been proposed [1]. The main goal in the sensorless control of an AC machine is the estimation of the rotor flux vector and in the case of speed sensorless control estimation of both rotor flux and speed. The idea is in using sliding-mode rotor flux observer for estimation of electromotive force of the machine that is used to improve switching strategy. The cascade current control is designed using Direct Current Control implemented in FPGA using Event driven approach, which significantly improves the speed of current-control loop and consequently the drive performance.

      Traditionally, the discrete time current controller is connected to the event driven inverter through the modulator, which represents a kind of adapter from time to the event driven control. Carrier based PWM and Space-Vector modulation are usual modulator solutions [1],[2]. Hysteresis controllers can be a good alternative to this solution as they are robust to system parameter variations, exhibit very good dynamics and are very easy for implementation [13],[14]. Their main drawback is a limited control of transistor switching frequency. Usually, three independent hysteresis controllers for a three phase current-controlled VSI are used. Another drawback of multivariable hysteresis control structures is in their complexity for use in more complicated structures, such as three phase inverter. In this paper, hysteresis comparators are used to convert continuous current values into the logic signals. Logic signals represent the conditions for switching of power inverter transistors and introduce a kind of event driven control. Transistor switching frequency is partly controlled by the prescribed sequence of transistor switching, which is determined by the designed switching strategy.

      The paper is organized as follows: first, the PMSM dynamics and control objectives are listed. The key issue of sensorless torque and speed control is properly designed observer for the PMSM rotor position and speed acquisition, which is described next. Major attention is paid to the current control design constructed as Direct Current Control. Further, the results of computer simulations are presented as well as the experimental setup. The conclusion highlights and discusses the main contribution of the paper and envisages the future work.

Machine Dynamics and Control

      The vector - controlled system for PMSM drive with non-salient poles is based on the motor differential equations written in the stationary coordinate system (a,b).

      The meaning of the symbols in eq. (1) is as follows:

– The stator voltage;

– The stator current;

– Electromotive force;

– The stator flux;

– The rotor flux;

– Load torque;

– Rotor flux angle;

– Excitation of permanent magnet;

– Stator resistance;

– Stator inductance;

– Number of pole pairs;

– System inertia;

      The proposed cascade control including rotor flux observer presented in Fig. 1 is designed to assure fast dynamic responses in transient states, a minimal current variation in the steady state and a stable behavior in the case of R-L parameter operating variations. The twofold structure is composed from discrete time driven dynamics on the DSP, while the current control is implemented using event-driven approach [15],[16]. The current control is designed based on the Direct Current Control (DCC). Reference signals are obtained using the control algorithm in rotor field coordinates. Rotor field and speed is obtained using rotor flux observer.

Figure 1 - Rotor Field Oriented Speed Control

Closed loop "EMF" and rotor flux observer

      The majority of speed identification methods are based on the approximated fundamental model of the machine. The use of stator equations, particularly the integration of the stator voltage vector is common for all methods. Its solution is fairly accurate when the switched stator voltage waveform is measured at high bandwidth, and when the parameters that determine the contributions of the resistive and the leakage voltage components are well known. As the influence of these parameters dominates the estimation at lower speed, the steady state accuracy of speed sensorless operation tends to be poor in the lower speed region. The dynamic performance depends on the accuracy of field angle estimation.

      Observer is based on the model of the PMSM where the derivation of the estimated stator flux is calculated from measured stator voltage and current [9]. Measured values of the stator voltage are used instead of using the reference voltage in order to avoid voltage error influence due to the power stage non linear behavior.

Figure 2 - Rotor flux observer

      The non-modeled dynamics is set as remaining voltage signal that is calculated from magnitude error of the rotor flux. The open integrator is closed by controlling the amplitude of the estimated rotor flux obtained from stator flux. The estimated value used for zero speed and low speed convergence is obtained from the closed - loop rotor flux observer. The estimated transformation angle is calculated using estimated rotor flux. The switching function of the VSC controller Cr is set to the error of estimation of the rotor flux to improve performance at low speed.

The discrete form of the resulting unknown offset voltage is:

Approximation of EMF with better signal/noise ratio used to achieve better switching strategy of DCC is expressed in stationary coordinates using observed rotor flux.

      Successful estimation of the rotor flux is based also on the knowledge of the stator voltages that can be obtained by measuring while using the stator voltage measurement unitus. The principle of measurement is based on integration of the instantaneous branch voltages and averaging the result over the discrete observer period [10]. Estimated speed is obtained by using a general algorithm for speed estimation [8].

Sector estimator

      In order to reduce switching losses, optimization of the switching sequence is introduced in the current controller. Appropriate sector is selected based on prediction of the stator voltage. When neglecting voltage drop on the inductance, stator voltage can be calculated by using calculated induced voltage and voltage drop on the resistance.

      Appropriate voltage sector is obtained by calculating the angle of the voltage vector using arctg function. Introduced p /6 offset simplifies the proposed Direct Control Controller algorithm which is described in following section.

Event-driven Direct Current Controller

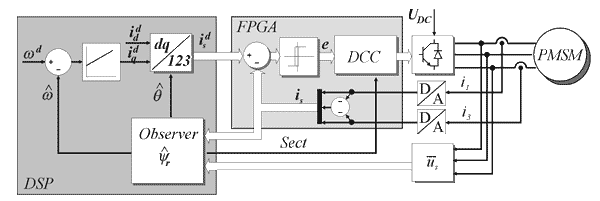
      The traditional current control scheme consisting of discrete time current controller and pulse-width modulator is replaced with new event-driven Direct Current Controller (DCC), which evaluates the transistor switching patterns of inverter directly from the phase current errors ia, ieb, iec and stator voltage sector Sect. The stator voltage sectors are determined as depicted in Fig.3.

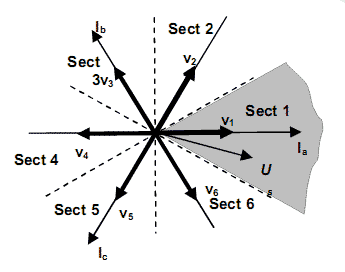
Figure 3 - Stator voltage Us sector allocation

      Considering the situation in Fig. 3, the stator voltage Us space vector is in sector 1. In this sector voltage vectors v0, v7, v2 and v6 are selected for the current control. Vectors v0, v7 are two zero vectors, while v2, v6 are two nearest adjacent live output voltage vectors to the sector 1. Sequential switching among these vectors is determined by instantaneous current error vector ie sector, as allocated in Fig 4. According to the instantaneous current error vector ie sector, the voltage vector vi is selected which has the greatest influence on the elimination of the error, similar to Direct Torque Control (DTC) control approach.

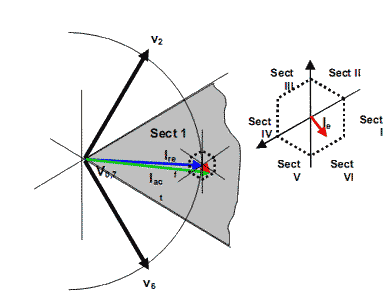
Figure 4 - Current error ie sector arrangement

      Considering inherent on-off switching functionality of the inverter, the modulator can be designed as Discrete Event-driven System (DES). Four output voltage vectors v0, v7, v2 and v6 are considered as discrete states of the system. The events for the transition among discrete states are determined by combination of phase current errors iea, ieb and iec. Consequently, the current control functionality is integrated directly into the modulator. The structure of the proposed strategy for sector 1 is represented by Petri Net graph [1 1],[12](Fig. 5). Switching among zero and live vectors (transitions T1, T2, T4, T5, T6 and T8) is determined by signs of current errors iea and -iec. The switching among live vectors (transitions T3 and T7) is determined by the sign of current error ieb. Similar control strategy is applied for the remaining sectors.

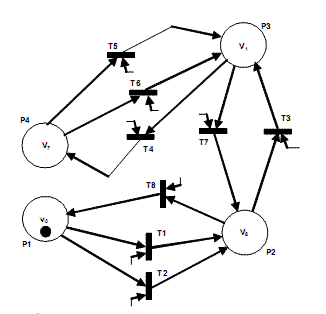
Figure 5 - PN-graph of EDCCM in Sector 1

      For the design, simulation and implementation purposes, PN-graphs are replaced by the matrix description of DES [16], which is schematically depicted in Fig. 6. Inputs, events, discrete states and outputs are denoted by logical variables u, x, m and y, respectively. m0 denotes initial discrete state.

      The structure of the system is described by logical matrices In, S, F and Out, representing relations among inputs u and events x, events x and states m and states m and outputs y, respectively.

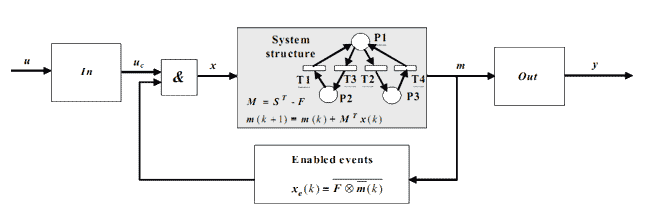
Figure 6 - Matrix description of DES system

Simulations

      The proposed observer and controller performance was tested with both simulations and experimental system. Simulations were performed using MATLAB / Simulink on parameters of 0.8 kW PMSM AMG6308. Designed direct current controller modeled by proposed matrix-based approach was simulated using Matlab/Simulink. A Permanent Magnet Synchronous Machine (PMSM) was used as load connected to the three phase VSI. The scope of the simulation was to control the PMSM in the speed mode using the PI speed-controller and proposed direct current controller. The simulation scheme is illustrated in Fig. 7.

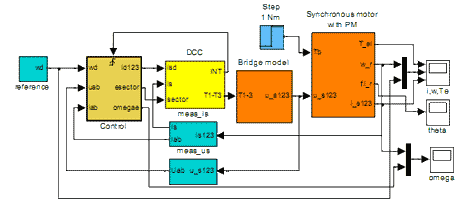
Figure 7 - The simulation scheme

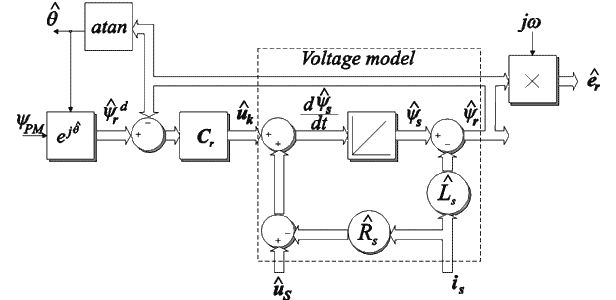
      Phase currents and voltages are measured, while the speed and position is calculated using rotor flux observer. The estimated drive speed is used for the speed control-loop, which is implemented by PI-controller and generates the q-component of the reference current in the d-q reference frame. The d-component of the reference current is set to 0. To comply with the designed current controller, the reference current is transformed from d-q to the a-b-c reference frame where it is denoted as id123. Actual load current is123 is measured directly from the phase lines using current transducers and fed back to the current controller. The current controller outputs are the signals for the control of transistors. Fig. 8 - 11 are showing the simulation results at low speed operation. The drive is started without load and accelerates to the reference speed. At the time 0.3 s the load is applied to the drive. Figure 8 shows the phase currents, where the current ripple can be noticed. Fig. 9 illustrates estimated rotor flux angle obtained from sliding mode rotor flux observer. The angle of the induced voltage calculated from voltage estimator differs from induced voltage angle during the load especially zero speed operation, therefore only information about induced voltage is not sufficient for sector determination as shown in Fig. 9. The speed observer successfully follows the real values while drive is reversed as shown in Fig. 10 even at speed reversing. Produced electrical torque is depicted in Fig. 11.

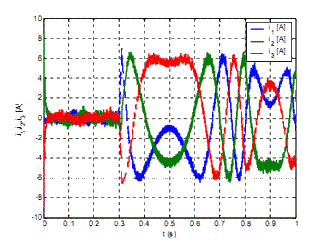
Figure 8 - Phase currents during the transient

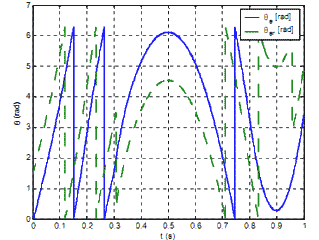
Figure 9 - Observed rotor angle and estimated angle of stator voltage

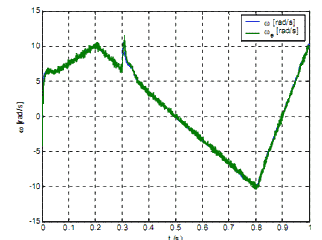
Figure 10 - Actual rotor speed w and observed rotor speed we during transition

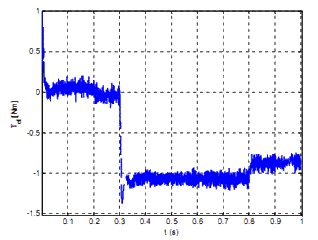
Figure 11 - Produced electrical torque

Experimental setup

      Experimental setup, similar to [15], was configured to verify simulation results. It is implemented on DSP2 board [17], which includes the DSP TMS320C32 floating point DSP and Xilinx XCS40PQ240 FPGA. The speed control algorithm and sliding-mode rotor flux observer of the PMSM are implemented on the DSP processor coded in C language, where algorithm execution time was set to the switching period 166 ms. The cascade current control is designed using event-driven Direct Current Control implemented in FPGA. The algorithm is designed as DES and described using logical matrices. Both the DES matrices and algorithm from Fig. 6 are included directly in the VHDL code for FPGA.. FPGA also hosts the implementation of the interface for measurement of the phase voltages and two phase currents. The phase current error is calculated and converted into logical values for DES algorithm using comparators with hysteresis, which is also implemented in FPGA. A/D conversion is the most critical operation of the Direct Current Controller regarding time and takes 2.7 ös. According to the fact, that A/D conversion takes most of the calculation time, while the calculation of the current error, hysteresis comparators and DES algorithm takes less then 166 ns. The proposed approach replaces usual sequential calculation of algorithms on the DSP by parallel executable hardware.

Conclusion

      Sensorless control of PMSM based on unique sliding - mode flux observer is presented in this paper. Sliding mode rotor flux observer based on PMSM model is used to obtain rotor position and speed. Rotor speed is estimated using observed angle of rotor. Initial rotor position is obtained by rotor position detection procedure. Operating range of sensorless control is extended using sliding-mode controller that extends the described features with robustness on parameter variation. Direct Current Control is used to integrate the functions of current controller and modulator. It is designed as event-driven system and represented using a novel matrix based description for such systems. Matrix description is used for implementation on FPGA, which allow higher switching frequency, comparing to the conventional PWM. The simulations confirmed potentials of the presented approach, although some optimization should be performed. Some potentials of suggested approach were already confirmed by experiments on FPGA devices for similar setup [15], where high switching frequencies (up to 200 kHz) were reported. This paper presents also the experimental setup for the sensorless torque and speed control of PMSM.

References

[1] J. Holtz, "Pulsewidth Modulation – A Survey," IEEE Transactions on Industrial Electronics, vol.39, No.5, December 1992, pp. 410-420

[2] K. Zhou, D. Wang, "Relationship Between Space-Vector Modulation and Three-Phase Carrier-Based PWM: A Comprehensive Analysis," IEEE Transactions on Industrial Electronics, vol.49, No.1, Februar 2002, pp. 410-420

[3] J. Holtz, "Methods of Speed Sensorless Control of AC drives", Sensorless Control of AC Motors, IEEE Press Book, (1996)

[4] V.I. Utkin, "Sliding mode control design and chattering problem", Electrotechnical Review, Ljubljana (SLO) 1993, vol.60, no.2-3, pp.75-81

[5] Z. Chen, "Sensorless Control of Interior Permanent Magnet Synchronous Motor by Estimation of an Extended Electromotive Force", IEEE Transaction on Industrial Electronics.

[6] T. Chin, M. Nakano, T. Hirayama, Accurate Measurement of Values of Voltage, Current and Power for Power Electronics Circuits, IEEE Transactions on Industry Applications, Tokyo, Japan, 1998.

[7] K. Jezernik, "Speed sensorless control of IM." V: PINDADO RICO, Rafael (ed.). Seminario anual de automática y electrónica industrial e instrumentación 2000, 13, 14 y 15 de septiembre de 2000. Barcelona: Universitat Politécnica de Catalunya, 2000, pp. XXIII-XXXII.

[8] L. Harnefors, H.-P. Nee "A general algorithm for speed and position estimation of ac motors" IEEE Trans. Ind. Electron., Feb. 2000, p. 77-83.

[9] H. Rasmussen, P. Vadstrup, H. Borsting “Adaptive observer for speed sensorless PM control”, IEEE IAS2003, Salt Lake City, Utah USA, October 2003

[10] Gregor Edelbaher, Evgen Urlep, Milan Curkovic, Valentin Kranjec, "Low speed performance improvement in sensorless drive using measured stator voltages of PWM voltage source inverter", V: Proceedings, International conference on industrial technology [also] IEEE ICIT 2003, Hotel Habakuk Maribor, Slovenia, December 10-12, 2003, Piscataway, IEEE, 2003, str. 542-547. [COBISS.SI-ID 8486166]

[11] Peterson J.L. “Petri Net Theory and the Modeling of Systems”, Prentice-Hall, New Jersey. 1981

[12] T. Murata. Petri nets: Properties, analysis and applications. Proceedings of the IEEE, 77(4):541--580, April 1989

[13] Rossi C., Tonielli A., “Robust Current Controller for Three-Phase Inverter Using Finite State Automaton”, IEEE Trans. On IE, Vol. 42, No. 2, pp. 169-178, 1998.

[14] Tilli A., Tonielli A., “Sequential design of Hysteresis Current Controller for Three-Phase Inverter”, IEEE Trans. On IE, Vol. 45, No. 5, pp. 771-781, 1998.

[15] Polic, A., Rodic M., Jezernik K., “Matrix based approach to overall functionality description of drives”. International power electronics and motion control conference, 2 - 4 September 2004, Riga, Latvia. EPE-PEMC 2004

[16] Polic, A., Jezernik K.,“Closed-Loop Matrix Based Model of Discrete Event Systems for Machine Logic Control Design”, IEEE Trans. on Industrial Informatics, vol. 1, Feb. 2005, pp. 39-46

[17] D. Hercog, M. Curkovic, G. Edelbaher and E.Urlep, “Programming of the DSP2 board with the Matlab/Simulink”, Proc. of IEEE ICIT 2003,