Электричество - 1998. - №12. - С. 23-27.
Предложен новый метод определения локальных дефектов и степени их развития в изоляции силовых кабельных линий 6-10 кВ. Метод предусматривает зондирование кабельных линий гармоническими колебаниями разной частоты и основан на теории длинных линий. Ключевые слова: кабельная линия, локальные дефекты, зондирование, теория длинных линий
A new method is proposed for determining local defects and the degree of their development in the insulation of 6—10 kV power cable lines. The method is based on the theory of long lines and involves sounding of cable lines with harmonic oscillations of varying frequency. Key words: cable line, local defects, sounding, theory of long lines
Одной из главных причин отказов кабельных линий является повреждение изоляции вследствие возникновения и роста в ней локальных дефектов, возникающих при изготовлении, монтаже и эксплуатации кабелей. В кабелях с бумажной изоляцией и вязкой пропиткой возможно появление локальных дефектов в виде газовых включений как в процессе производства, так и эксплуатационных условиях. Наличие газовых включений приводит к появлению частичных разрядов, которые, в свою очередь, ведут к росту локальных дефектов. В кабелях с полиэтиленовой изоляцией под действием частичных разрядов образуются локальные дефекты, представленные ветвистыми побегами - дендритами [1]. Существующие методы контроля изоляции выявляют, в основном, распределенные дефекты, поэтому определение локальных дефектов в кабельной изоляции является весьма актуальной задачей.
Локальный дефект кабельной изоляции может быть представлен конденсатором с емкостью СВ, меньшей емкости неповрежденной изоляции С (рис. 1).
Известны методы измерения входного сопротивления длинной линии на высоких частотах [2,3]. В данной статье предлагается методика определения технического состояния изоляции кабельных линий, базирующаяся на анализе за висимости входного сопротивления от частоты.
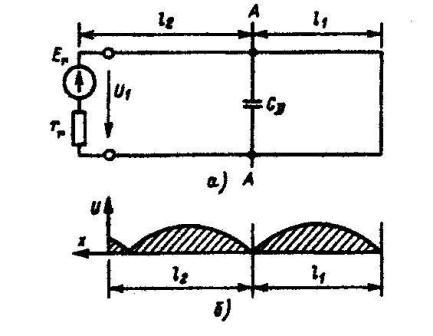
Теоретические положения. Рассмотрим кабель длиной l, который представим длинной линией, имеющей один локальный дефект изоляции
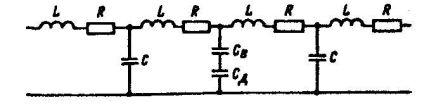
Рис 1. Схема замещения изоляции кабеля при наличии в ней
локального дефекта в виде газового включения; СД -емкость диэлектрика, расположенного последовательно с включением;
СВ - емкость включения;С - емкость неповрежденной изоляции
в виде емкости
в виде емкости
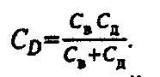
Если на вход длинной линии (см. рис.2,а), закороченной на конце,
подать напряжение высокой частоты, то в ней установится режим стоячих волн. Эпюра распределения напряжения
вдоль линии на этой частоте показана на рис. 2,б. Частоту, на которой напряжение равно нулю (узел напряжения),
можно определить из условий
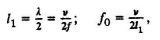 (1)
(1)
где n - фазовая скорость распространения; f - частота генератора;
l - длина волны.
При увеличении частоты генератора количество узлов также увеличивается. Их координаты, отсчитываемые от конца линии, можно найти по формуле
При увеличении частоты генератора количество узлов также увеличивается. Их координаты, отсчитываемые от конца линии, можно найти по формуле
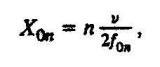 (2)
(2) где n = 1, 2, 3, ... - количество узлов; f0n-частота, при которой напряжение равно нулю. Частоты, на которых узлы будут накрывать дефект, находятся на расстоянии l1 от конца линии и определяются также из условия
 (3)
(3)
На этих частотах распределение напряжения в линии с дефектом будет таким же, как и в линии без дефекта. На других частотах дефект будет изменять картину распределения и нарушать режим стоячих волн. Наибольшее влияние дефекта на распределение напряжения в линии будет на частотах, соответствующих пучности напряжения. Самая низкая частота fn , на которой возникает это влияние, может быть найдена из условия
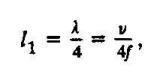 (4)
(4)тогда
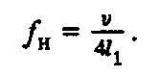 (5)
(5)Более высокие частоты, на которые приходится пучность (максимум) напряжения, можно найти из выражения
 (6)
(6)Поскольку распределение напряжения в линии получить экспериментальным путем довольно трудно, то о состоянии изоляции кабеля можно судить на основе анализа данных измерений входного сопротивления линии.
Если измерить на входе короткозамкнутой линии напряжение UВХ, ток IВХ и разность фаз между ними jZ , то можно определить входное сопротивление:
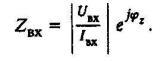 (7)
(7)
Зная входное сопротивление, можно найти
коэффициент отражения на входе линии:
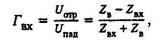 (8)
(8)где UОТР - напряжение oтраженной волны; UПАД - напряжение падающей волны; ZB - волновое сопротивление линии.
Теоретический анализ и компьютерное моделирование показали, что коэффициент отражения может быть представлен в виде произведения четырех сомножителей:
 (9)
(9)где ГD - коэффициента отражения.
Для идеальной линии, закороченной на конце, коэффициент отражения на входе линии определяется выражением
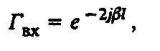 (10)
(10)где b=2p/l=w/u
Величина 2bl характеризует набег фазы от раженной волны. Для идеальной линии |UОТР| = |UПАД|. Для линии с распределенными потерями коэффициент отражения равен [2]
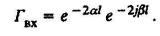 (11)
(11)Первый сомножитель (11)
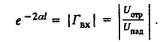 (12)
(12)Из (12) найдем коэффициент a
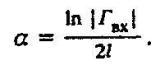 (13)
(13)Для линии, имеющей дефект реактивного характера, отношение UОТР/UПАД имеет такую же величину, как и в выражении (12), так как реактивный дефект не поглощает энергии. Однако реактивный дефект даст дополнительный набег фазы aD . Величина этого дефекта зависит от того, накроет ли его узел напряжения или нет, т.е. зависимость aD отf должна иметь волновой характер и ее максимум достигается при выполнении условия (6).
Если дефект будет иметь диссипативную составляющую, т.е. будет поглощать часть энергии волны, то сомножитель в (9) будет удовлетворять условию
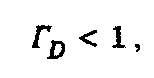 (14)
(14)в противном случае ГD = 1, т.е. координаты узла напряжения будут совпадать с координатой дефекта. Таким образом, следует, что величина ГD имеет волновой характер, достигая экстремального значения на частотах, определяемых условием (3).
Расчетная часть. Была смоделирована на компьютере длинная линия с одним локальным дефектом диссипативного характера. Была поставлена задача определения:
местонахождения дефекта в кабеле;
характера (вида) дефекта;
величины (степени развития) дефекта.
Ко входу кабеля, закороченного на конце, подключим генератор высокочастотных колебаний. Измерив входной ток IВХ , напряжение UВХ и разность фаз между ними a найдем входное сопротивление кабеля ZВХ по формуле
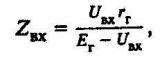 (15)
(15)где rГ - внутреннее сопротивление генератора.
Коэффициент отражения на входе кабеля (линии) можно определить по выражению (8), которое можно представить в виде
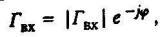 (16)
(16)где a=2bl
Для регулярной линии без потерь|ГВХ| = 1. В регулярной линии с потерями
 (17)
(17)Если линяя без потерь имеет реактивный дефект, то отраженная волна получит дополнительный набег фазы aD и тогда
 (18)
(18)в этом случае выражение (16) можно записать как
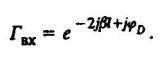 (19)
(19)Логарифмируя (19), получаем
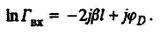 (20)
(20)Если дефект имеет активную составляющую, то ln<|ГВХ|<0. В этом случае величина Rе(lnГВХ) будет иметь периодический характер, анализируя который можно получить информацию о местоположении дефекта и величине его проводимости GD. При этом (20) примет вид
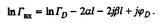 (21)
(21)Мнимая часть (21) Im(lnГВХ)содержит информацию о набеге фазы, вызванном дефектом. На основе расчетов на рис. 3 построена зависимость набега фазы от частоты генератора: f1=f/f0, где f0=u/2l для кабеля с волновым сопротивлением ZB=50 Ом. Изменение кривой полученного графика (в области частот от 6,8 до 10) свидетельствует о наличии дефекта в изоляции кабеля. Однако определение местонахождения этого дефекта по длине кабеля вызывает затруднения.

Рис. 3. Зависимость мнимой части логарифма коэффициента отражения от частоты генератора
Из (20) найдем
 (22)
(22)На рис. 4 (кривая 2) представлена зависимость aD от частоты. Из графика видно, что aD имеет периодический характер. Функция aD (f) имеет экстремумы на тех частотах, на которых узел напряжения в линии накрывает дефект. В этом случае распределение напряжения в линии с дефектом будет подобно распределению напряжения в линии без дефекта. Первый минимум дефекта aD определится из условия
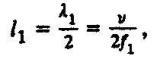 (23)
(23)второй минимум - из условия
 (24)
(24)тогда n - й минимум можно определить из выражения
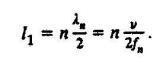 (25)
(25)Таким образом, анализируя график aD можно определить l1 , т.е. расстояние от конца линии до дефекта. Можно заметить также, что частоты f1 , f 2 соответствуют минимальному значению входного сопротивления ZВХ(рис. 4, кривая 1). Действительная часть Rе(lnГВХ) =-2al+lnГD представлена кривой 3 рис. 4. Мы видим, что график имеет волновой характер. Минимумы потерь соответствуют частотам, определяемым условием (3). Величину дефекта (CD - емкость дефекта, GD - проводимость дефекта) можно определить следующим образом. Проводимость участка ка бельной линии от ее конца, включая дефект, можно определить как
 (26)
(26)где G1 = G0thg входная проводимость в сечении АА (рис. 5); G0 - погонная проводимость линии; w=2pf угловая частота; g - коэффициент распространения.

Рис. 4. Кривые изменения:1 - входного сопротивления; 2 - набега фазы, вызванного дефектом; 3 - коэффициента затухания от частоты
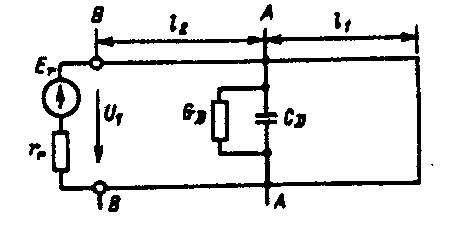
Рис. 5. Схема линии с дефектом, представленным активной проводимостью и емкостью
Входное сопротивление линии в сечении ВВ (рис. 5) может быть вычислено по формуле
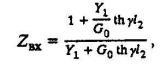 (27)
(27)где l2 - длина участка линии от входа до дефекта.
Найдем Y1 из (27):
 (28)
(28)Тогда величину и характер дефекта можно определить из (26) с учетом (28)
 (29)
(29)Таким образом, анализ зависимости входного сопротивления закороченной линии на различных частотах позволяет выявлять не только местоположение локального дефекта, но и оценить его величину и характер.
1. Кучинский Г.С. Частотные разряды в высоковольтных конструкциях. – Л.; Энергия, 1979.
2. Афанасьев Б.П., Гольдин О.Е., Кляцкин И.Г. / Теория линейных электрических цепей. - М.: Высшая школа, 1973.
3. Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1973.