Перевод: Лысиковой С. В.
В БИБЛИОТЕКУ
Аннотация—в этой статье представлен модифицированный метод измерения сопротивления ротора с железным стержнем в трех фазных двигателях с клеткой, отлитой из меди. Необходимо детально разработать новый метод определения этого активного сопротивления, так как величины различных частей ротора имеют иное соотношение в литом медном роторе, то есть величина сопротивления листа электро-технического железа является существенной для значения сопротивления стержень-железо. Смоделированный автором образец представленный на ИКЭМ 96 не отвечает требованиям этого вида ротора. Итак в этой статье предлагается новая физическая модель ротора, новая схема замещения, новая система дифференциальных уравнений и решение их. Здесь представлены результаты опытных исследований.
1. ВВЕДЕНИЕ
Экспериментально полученное значение сопротивления железного стержня ротора может быть использовано, как для расчета потерь в роторе, частично влияющих на потери в нагрузке, так и для определения эффективности применения отливки ротора. Значение очень интересно для новых технологий отливки, например отливки меди, где значение уже известно.
Но известные методы не являются эффективными в этом случае из-за различного отношения физических величин в роторе, по сравнению с ротором с алюминиевой клеткой. Итак, был разработан усовершенствованный метод для определения сопротивления железного стержня ротора с клеткой из меди. Модификация схожа с методом измерений Одока [1], усовершенствована предварительно автором статьи [6] для ротора с алюминиевой клеткой.
Здесь представлены результаты экспериментальных расчетов сопротивления ротора с железным стержнем отлитого из меди и для сравнения роторов, отлитых из алюминия, рассчитанного разными методами, в том числе и модифицированным.
Анализы падения напряжения между кольцом и стержнем ротора, сделанные методом Одока позволяют оценить качество литья.
2. МЕТОДЫ И ИЗМЕРЕНИЯ ЦЕПЕЙ ДЛЯ ОПРЕДЕЛЕНИЯ СОПРОТИВЛЕНИЯ В ПОПЕРЕЧНОМ СЕЧЕНИИ
Методы измерения для расчета сопротивления в поперечном сечении могут быть разделены на 2 группы:
-методы, которые не требуют разрушения ротора,
-методы, которые требуют разрушения (передвижение колец или разрезание их).
К первой группе можно отнести:
А. Метод Одока [1];
В. Метод Динка [3];
С. Метод Дабала [6];
Ко второй:
D. Метод Сичанека [2];
Е. Метод Кристофайдса [4];
F. Метод Тока и другие. [5].
А. Метод
Это практическое измерение сопротивления ротора с железным стержнем rq, сделанное по диаграмме на рис.1.
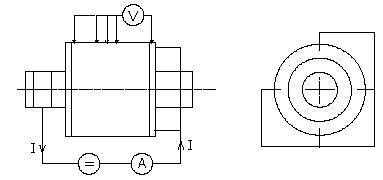
Рис.1 Измерительная диаграмма метода Одока –А.
Сопротивление rq вычисляется по формуле

где:
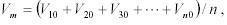
I – общий ток, протекающий сквозь клетку;
Z2– количество пазов ротора;
lFe – длина железного стержня в роторе.
В. Метод
Измерительная диаграмма такая же, как и в методе А. Метод В заключается в рассмотрении погрешности из-за падения напряжения в стержнях:

где:
VPQ-падение напряжения на длине стержня.
С. Метод
Метод усовершенствует метод Одока. Он базируется на однородной продолжительной проводимости сети. Этот метод детально представлен в [6].
D.Метод
I Создан на основе первого метода, который требует разрушения ротора, разрезаний колец. Измерительная диаграмма представлена на рис.2
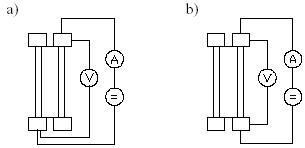
Рис.2 Измерительная диаграмма метода Сиганека
Сопротивление первого стержня и двойное сопротивление в поперечном сечении между стержнем и сопротивлением Rc определяется рис.2а). Сопротивление стержня Rt в рис.2б). Двойное сопротивление поперечного сечения определяется, как

Общее контактное сопротивление на поверхности стержня:

где с-периметр пересечения стержня , l-длина железного стержня.
E. Метод
Этот метод отличается от метода D перестановкой колец клетки. Провода прикручиваются к концам смежных проводов.
F. Метод
Это усовершенствованный метод Сиганека. Влияние на сопротивление стержня, когда Rm>> R1 может быть представлено, как

где Rm< R1 вычисляется по формуле
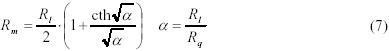
и после решения этого уравнения возможно найти значение Rq.
Символы Rq, Rm, Rl заменяются соответственно на R2p, Rc, Rl в методе Сиганека.
3.МОДИФИЦИРОВАННЫЙ МЕТОД ВЫЧИСЛЕНИЯ СОПРОТИВЛЕНИЯ В ЖЕЛЕЗНОМ СТЕРЖНЕ РОТОРА, ОТЛИТОГО ИЗ МЕДИ.
Модифицированный метод схож с методом Одока (Рис.1 и Рис.3). Это усовершенствование метода Дабала, в котором учитывается сопротивление листов электротехнического железа между стержнем и валом в случае ротора отлитого из меди. В этом методе принимается, что клетка симметрична и соответственно физическая модель является однородной сетью с длительным распространенным параметрическим удельным сопротивлением (Рис.4)
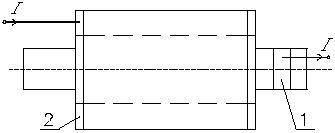
Рис.3 Измерительная диаграмма сопротивления между стержнем ротора и сердечником в соответствии с методом Одока.
1-медный обод с выводом;
2-кольцо ротора.
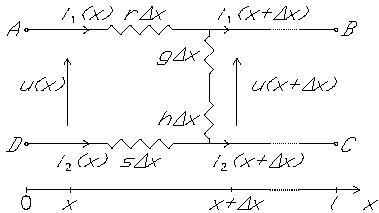
Рис.4 Эквивалентная цепь для диаграммы на рис.3
Символы: r - удельное сопротивление стержня на единицу длины, s - удельное сопротивление вала на единицу длины, q-контактная проводимость на единицу длины, h-листовая проводимость электротехнического железа, х-координата, х-элементарный участок цепи, l-длина железного ротора, i(x)-ток, u(x)-напряжение.
На основе схемы замещения рассчитывается следующая система дифференциальных уравнений:
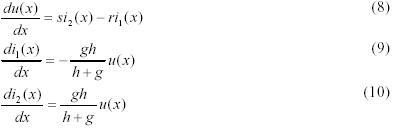
Начальные условия задаются так

T Решением системы уравнений соответствующей начальным условиям (11)-(13) является выражение
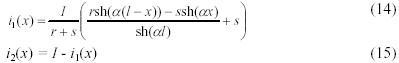
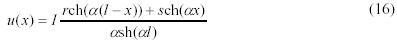
Входное сопротивление Rm от питания равно
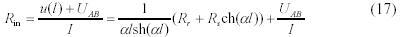
в котором напряжения между концами стержня
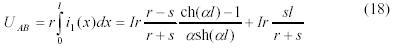
с другой стороны
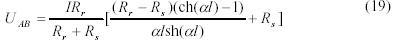
где
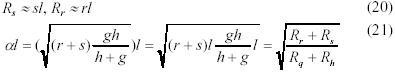
В этом случае сопротивление поперечного сечения равно

и сопротивлению листового электротехнического железа.

Дополнительно рассчитывается напряжение UAD.
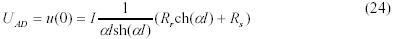
Существуют несколько возможных алгоритмов для расчета сопротивления поперечного сечения Rg , например при помощи UAD, UAB или других измерительных напряжений, для которых известны формулы. Один из алгоритмов приведен ниже.
Алгоритм определения Rg в методе С.
1.Значение тока в (18) или (19) будет взято равными I/Qr, где I-измеренный общий ток, протекающий сквозь ротор, Qr –количество падений напряжения ротора.
2.На основе измеренного напряжения UАВ, ток I/Qr и найденные значения сопротивления стержня Rr, сопротивление вала Rg, сопротивление листового электротехнического железа Rh (все вычислены на основе измерений и констант вещества) будет рассчитан параметр l из (18) или (19) .
3.Из (21) определяем искомое сопротивление поперечного сечения Rg.
4. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
Были изучены 6 роторов с 4 мя полюсами, с двумя весами валов (112мм, 160мм) двигателей. Три ротора были отлиты из меди и три из алюминия.
Измерения производились вдоль 7 зубцов (1/4 периметра) каждого ротора между зажимами, проводящими ток. Результаты измерений, полученные тремя методами без разрушения (А, В, и С) представлены в табл.1 и на Рис.5-8.
Таблица 1. Результаты измерения сопротивления в железном стержне ротора.
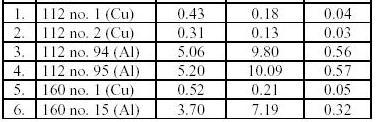
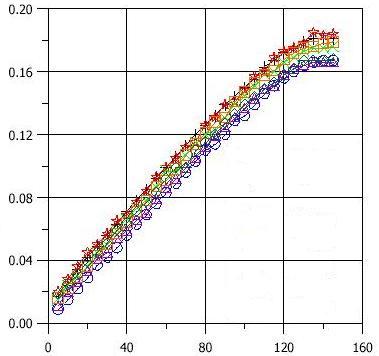
Рис.5 .Кольцевые зубцы падения напряжения вдоль сердечника ротора двигателя 112 №1 (меди) для 7 зубцов, направление тока положительное.
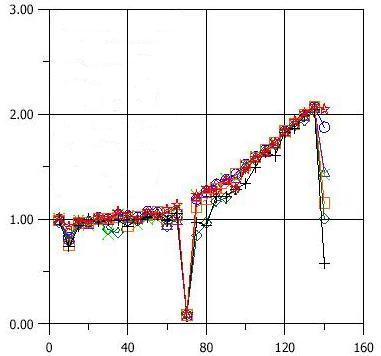
Рис.6.Кольцевые зубцы падение напряжения вдоль сердечника ротора двигателя 112 №34 (алюминий) для 7 зубцов, направление тока положительное (при сильном падении напряжения в центре ротора, отлитого из алюминия, кольцо появляется в этом роторе).
Измерительная цепь состоит из источника постоянного тока (гальванический генератор UN=7 и IN=600А), амперметра с шунтом для измерения тока, общего вольтметра, присоединенного к компьютеру через IEEE 488 и дополнительное сопротивление для ограничения тока.
Значение тока было равно 100А. Провода были присоединены к кольцу при помощи 4-х выводов с одной стороны ротора и припаянных к меди ободу, зафиксированному на валу с другой стороны.

Рис.7 Круговые зубцы пазов напряжения вдоль сердечника ротора двигателя 100 №1 (Cu) для 7 зубцов, направление тока положительное.
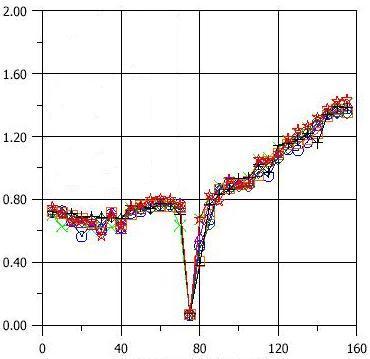
Рис.8 Круговые зубцы пазов И=И № 15(Аl) (глубокий паз в середине ротора определен Al кольцом, применяемым в этом роторе).
Результаты (Табл.1) отличаются в зависимости от метода и материала клетки.
Экспериментально-вычислительный метод Дабала дает результаты около 10 раз меньшие, чем методы Одока и Дика . Однако, должно быть принято к рассмотрению,что в методе Дабала взято реальное распространение токов вместо средних величин в методах Одока и Дика.
Но результаты из разных методов в итоге показывают, что различие в падении напряжения роторов
сделанных из меди намного меньше и имеют определенно меньший случайный характер. Это может значить,что медные клетки лучше для литья.
В различии падений напряжения роторов, отлитых из меди (Рис.5 и Рис.7) возможно увидеть, что различие в падении напряжения части зубцов согласованы с реальным распределяющимся током (зубец №1 и №7) были ближними к зажимам с токами и у них наибольший паз напряжения. Это явление не присутствует в роторах из Al (Рис.6 и Рис.8). В этом случае различия в падении напряжения смешаны.
В старом методе Дабала ( 6 ) эквивалентная цепь была представлена с допущением Rq >>Rh . В роторах . отлитых из Al это условие соблюдается, например, в роторе 112 №94 ( Al) R=3.95*10(-5). (Метод Дабала) и итак R h /R q=15% . В роторах отлитых из меди. Так что необходимо взять в рассмотрение сопротивление R h в эквивалентной цепи для роторов из меди.
5. ВЫВОДЫ
Модифицированный экспериментально-расчетный метод для определения сопротивления в роторе с железным стержнем и отлитой из меди клеткой дает более точные результаты, чем другие методы.
Результаты измерений определенно показывают, что значение сопротивления поперечного сечения в роторах с клеткой, отлитой из меди более чем в 10 раз ниже, чем в роторах с клеткой , отлитой из Al.
Потому что сопротивление в поперечном сечении меньше. Добавочные потери могут быть больше в роторах отлитых из меди.
Различие в напряжениях кольцо-зубец показывают, что сопротивление поперечного сечения в роторах с клеткой отлитых из меди имеет определенно случайный характер (иеньшее отклонение от средней величины), чем в роторах с клеткой, отлитой из алюминия. Это может значить, что лучше отлитые из меди клетки.
ССЫЛКИ
[1] A. M. Odok, "Stray-Load Losses and Stray Torques in Induction Machines," AIEE Trans. p. III, PAS., April 1958, pp. 43-53.
[2] L.Ciganek, "Kontaktnoe soprotivlenie mezdu sterznjami aluminievoj kletki i stal'ju paketa rotora, " Vestnik Elektropromyњlennosti, No 6, 1960, pp. 40-43.
[3] F. Ding F, "Improvements for the Odok Method to Measure the Cross Contact Resistance od a Squuirrel-Cage Rotor," IEEE Trans. on Electrical Machines and Power Systems, No. 1, 1987, pp. 61-71.
[4] N. Christofides N, "Origins of Load Losses in Induction Motors with Cast Aluminium Rotors," Proc. IEE, No. 12, 1965, pp. 2317-2332.
[5] G. Toke, P. L. Timar, P. Goszti, K. Toth, G. Vincz, "Experimental Determination of Tranverse Resistivity of Cast Aluminium Squirrel-Cage," Proc. ICEM, 1982, pp. 796-799.
[6] K. Dabala, "A New Experimental-Computational Method to Determine Rotor-Bar-Iron Resistance," Proc. of ICEM, Vigo (Spain), 10-12.09.1996, vol. II, pp. 69-72.
вверх
Аннотация—в этой статье представлен модифицированный метод измерения сопротивления ротора с железным стержнем в трех фазных двигателях с клеткой, отлитой из меди. Необходимо детально разработать новый метод определения этого активного сопротивления, так как величины различных частей ротора имеют иное соотношение в литом медном роторе, то есть величина сопротивления листа электро-технического железа является существенной для значения сопротивления стержень-железо. Смоделированный автором образец представленный на ИКЭМ 96 не отвечает требованиям этого вида ротора. Итак в этой статье предлагается новая физическая модель ротора, новая схема замещения, новая система дифференциальных уравнений и решение их. Здесь представлены результаты опытных исследований.
1. ВВЕДЕНИЕ
Экспериментально полученное значение сопротивления железного стержня ротора может быть использовано, как для расчета потерь в роторе, частично влияющих на потери в нагрузке, так и для определения эффективности применения отливки ротора. Значение очень интересно для новых технологий отливки, например отливки меди, где значение уже известно.
Но известные методы не являются эффективными в этом случае из-за различного отношения физических величин в роторе, по сравнению с ротором с алюминиевой клеткой. Итак, был разработан усовершенствованный метод для определения сопротивления железного стержня ротора с клеткой из меди. Модификация схожа с методом измерений Одока [1], усовершенствована предварительно автором статьи [6] для ротора с алюминиевой клеткой.
Здесь представлены результаты экспериментальных расчетов сопротивления ротора с железным стержнем отлитого из меди и для сравнения роторов, отлитых из алюминия, рассчитанного разными методами, в том числе и модифицированным.
Анализы падения напряжения между кольцом и стержнем ротора, сделанные методом Одока позволяют оценить качество литья.
2. МЕТОДЫ И ИЗМЕРЕНИЯ ЦЕПЕЙ ДЛЯ ОПРЕДЕЛЕНИЯ СОПРОТИВЛЕНИЯ В ПОПЕРЕЧНОМ СЕЧЕНИИ
Методы измерения для расчета сопротивления в поперечном сечении могут быть разделены на 2 группы:
-методы, которые не требуют разрушения ротора,
-методы, которые требуют разрушения (передвижение колец или разрезание их).
К первой группе можно отнести:
А. Метод Одока [1];
В. Метод Динка [3];
С. Метод Дабала [6];
Ко второй:
D. Метод Сичанека [2];
Е. Метод Кристофайдса [4];
F. Метод Тока и другие. [5].
А. Метод
Это практическое измерение сопротивления ротора с железным стержнем rq, сделанное по диаграмме на рис.1.

Рис.1 Измерительная диаграмма метода Одока –А.
Сопротивление rq вычисляется по формуле
где:
I – общий ток, протекающий сквозь клетку;
Z2– количество пазов ротора;
lFe – длина железного стержня в роторе.
В. Метод
Измерительная диаграмма такая же, как и в методе А. Метод В заключается в рассмотрении погрешности из-за падения напряжения в стержнях:

где:
VPQ-падение напряжения на длине стержня.
С. Метод
Метод усовершенствует метод Одока. Он базируется на однородной продолжительной проводимости сети. Этот метод детально представлен в [6].
D.Метод
I Создан на основе первого метода, который требует разрушения ротора, разрезаний колец. Измерительная диаграмма представлена на рис.2

Рис.2 Измерительная диаграмма метода Сиганека
Сопротивление первого стержня и двойное сопротивление в поперечном сечении между стержнем и сопротивлением Rc определяется рис.2а). Сопротивление стержня Rt в рис.2б). Двойное сопротивление поперечного сечения определяется, как
Общее контактное сопротивление на поверхности стержня:
где с-периметр пересечения стержня , l-длина железного стержня.
E. Метод
Этот метод отличается от метода D перестановкой колец клетки. Провода прикручиваются к концам смежных проводов.
F. Метод
Это усовершенствованный метод Сиганека. Влияние на сопротивление стержня, когда Rm>> R1 может быть представлено, как
где Rm< R1 вычисляется по формуле
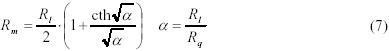
и после решения этого уравнения возможно найти значение Rq.
Символы Rq, Rm, Rl заменяются соответственно на R2p, Rc, Rl в методе Сиганека.
3.МОДИФИЦИРОВАННЫЙ МЕТОД ВЫЧИСЛЕНИЯ СОПРОТИВЛЕНИЯ В ЖЕЛЕЗНОМ СТЕРЖНЕ РОТОРА, ОТЛИТОГО ИЗ МЕДИ.
Модифицированный метод схож с методом Одока (Рис.1 и Рис.3). Это усовершенствование метода Дабала, в котором учитывается сопротивление листов электротехнического железа между стержнем и валом в случае ротора отлитого из меди. В этом методе принимается, что клетка симметрична и соответственно физическая модель является однородной сетью с длительным распространенным параметрическим удельным сопротивлением (Рис.4)

Рис.3 Измерительная диаграмма сопротивления между стержнем ротора и сердечником в соответствии с методом Одока.
1-медный обод с выводом;
2-кольцо ротора.

Рис.4 Эквивалентная цепь для диаграммы на рис.3
Символы: r - удельное сопротивление стержня на единицу длины, s - удельное сопротивление вала на единицу длины, q-контактная проводимость на единицу длины, h-листовая проводимость электротехнического железа, х-координата, х-элементарный участок цепи, l-длина железного ротора, i(x)-ток, u(x)-напряжение.
На основе схемы замещения рассчитывается следующая система дифференциальных уравнений:
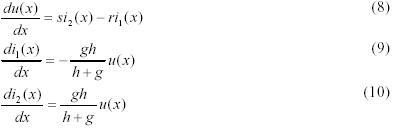
Начальные условия задаются так

T Решением системы уравнений соответствующей начальным условиям (11)-(13) является выражение
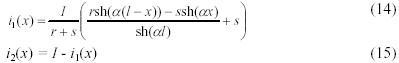
Входное сопротивление Rm от питания равно
в котором напряжения между концами стержня
с другой стороны
где
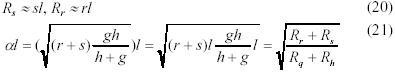
В этом случае сопротивление поперечного сечения равно
и сопротивлению листового электротехнического железа.
Дополнительно рассчитывается напряжение UAD.
Существуют несколько возможных алгоритмов для расчета сопротивления поперечного сечения Rg , например при помощи UAD, UAB или других измерительных напряжений, для которых известны формулы. Один из алгоритмов приведен ниже.
Алгоритм определения Rg в методе С.
1.Значение тока в (18) или (19) будет взято равными I/Qr, где I-измеренный общий ток, протекающий сквозь ротор, Qr –количество падений напряжения ротора.
2.На основе измеренного напряжения UАВ, ток I/Qr и найденные значения сопротивления стержня Rr, сопротивление вала Rg, сопротивление листового электротехнического железа Rh (все вычислены на основе измерений и констант вещества) будет рассчитан параметр l из (18) или (19) .
3.Из (21) определяем искомое сопротивление поперечного сечения Rg.
4. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
Были изучены 6 роторов с 4 мя полюсами, с двумя весами валов (112мм, 160мм) двигателей. Три ротора были отлиты из меди и три из алюминия.
Измерения производились вдоль 7 зубцов (1/4 периметра) каждого ротора между зажимами, проводящими ток. Результаты измерений, полученные тремя методами без разрушения (А, В, и С) представлены в табл.1 и на Рис.5-8.
Таблица 1. Результаты измерения сопротивления в железном стержне ротора.


Рис.5 .Кольцевые зубцы падения напряжения вдоль сердечника ротора двигателя 112 №1 (меди) для 7 зубцов, направление тока положительное.

Рис.6.Кольцевые зубцы падение напряжения вдоль сердечника ротора двигателя 112 №34 (алюминий) для 7 зубцов, направление тока положительное (при сильном падении напряжения в центре ротора, отлитого из алюминия, кольцо появляется в этом роторе).
Измерительная цепь состоит из источника постоянного тока (гальванический генератор UN=7 и IN=600А), амперметра с шунтом для измерения тока, общего вольтметра, присоединенного к компьютеру через IEEE 488 и дополнительное сопротивление для ограничения тока.
Значение тока было равно 100А. Провода были присоединены к кольцу при помощи 4-х выводов с одной стороны ротора и припаянных к меди ободу, зафиксированному на валу с другой стороны.

Рис.7 Круговые зубцы пазов напряжения вдоль сердечника ротора двигателя 100 №1 (Cu) для 7 зубцов, направление тока положительное.

Рис.8 Круговые зубцы пазов И=И № 15(Аl) (глубокий паз в середине ротора определен Al кольцом, применяемым в этом роторе).
Результаты (Табл.1) отличаются в зависимости от метода и материала клетки.
Экспериментально-вычислительный метод Дабала дает результаты около 10 раз меньшие, чем методы Одока и Дика . Однако, должно быть принято к рассмотрению,что в методе Дабала взято реальное распространение токов вместо средних величин в методах Одока и Дика.
Но результаты из разных методов в итоге показывают, что различие в падении напряжения роторов сделанных из меди намного меньше и имеют определенно меньший случайный характер. Это может значить,что медные клетки лучше для литья.
В различии падений напряжения роторов, отлитых из меди (Рис.5 и Рис.7) возможно увидеть, что различие в падении напряжения части зубцов согласованы с реальным распределяющимся током (зубец №1 и №7) были ближними к зажимам с токами и у них наибольший паз напряжения. Это явление не присутствует в роторах из Al (Рис.6 и Рис.8). В этом случае различия в падении напряжения смешаны.
В старом методе Дабала ( 6 ) эквивалентная цепь была представлена с допущением Rq >>Rh . В роторах . отлитых из Al это условие соблюдается, например, в роторе 112 №94 ( Al) R=3.95*10(-5). (Метод Дабала) и итак R h /R q=15% . В роторах отлитых из меди. Так что необходимо взять в рассмотрение сопротивление R h в эквивалентной цепи для роторов из меди.
5. ВЫВОДЫ
Модифицированный экспериментально-расчетный метод для определения сопротивления в роторе с железным стержнем и отлитой из меди клеткой дает более точные результаты, чем другие методы.
Результаты измерений определенно показывают, что значение сопротивления поперечного сечения в роторах с клеткой, отлитой из меди более чем в 10 раз ниже, чем в роторах с клеткой , отлитой из Al.
Потому что сопротивление в поперечном сечении меньше. Добавочные потери могут быть больше в роторах отлитых из меди.
Различие в напряжениях кольцо-зубец показывают, что сопротивление поперечного сечения в роторах с клеткой отлитых из меди имеет определенно случайный характер (иеньшее отклонение от средней величины), чем в роторах с клеткой, отлитой из алюминия. Это может значить, что лучше отлитые из меди клетки.
ССЫЛКИ
[1] A. M. Odok, "Stray-Load Losses and Stray Torques in Induction Machines," AIEE Trans. p. III, PAS., April 1958, pp. 43-53.
[2] L.Ciganek, "Kontaktnoe soprotivlenie mezdu sterznjami aluminievoj kletki i stal'ju paketa rotora, " Vestnik Elektropromyњlennosti, No 6, 1960, pp. 40-43.
[3] F. Ding F, "Improvements for the Odok Method to Measure the Cross Contact Resistance od a Squuirrel-Cage Rotor," IEEE Trans. on Electrical Machines and Power Systems, No. 1, 1987, pp. 61-71.
[4] N. Christofides N, "Origins of Load Losses in Induction Motors with Cast Aluminium Rotors," Proc. IEE, No. 12, 1965, pp. 2317-2332.
[5] G. Toke, P. L. Timar, P. Goszti, K. Toth, G. Vincz, "Experimental Determination of Tranverse Resistivity of Cast Aluminium Squirrel-Cage," Proc. ICEM, 1982, pp. 796-799.
[6] K. Dabala, "A New Experimental-Computational Method to Determine Rotor-Bar-Iron Resistance," Proc. of ICEM, Vigo (Spain), 10-12.09.1996, vol. II, pp. 69-72.