Автореферат Онищенко О.С. Оценка живучести подстанции 110/35/10 кВ, которая снабжает электроэнергией промышленные предприятия

Впервые в мире понятие живучести было сформулировано русским адмиралом Степаном Осиповичем Макаровым - это способность судна продолжать бой, имея повреждения в различных боевых частях [1].
В энергетике под живучестью понимается свойство объекта противостоять возмущениям, не допуская их каскадного развития с массовым нарушением питания потребителей [2].
Толчком к развитию методов оценки надежности систем электроснабжения и прогнозирования цепочечных аварий в энергосистемах (ЭС) послужила авария, случившаяся 9 ноября 1965 года в США, которая привела к тому, что на территории с населением около 30 млн. человек более чем на 10 часов была прекращена подача электроэнергии. Ущерб от аварии составил более 100 млн. долларов. Последовавшие после этого десяток мелких (с экономической точки зрения), но подобных аварий по стране завершились 13 июля 1977 года аварией в Нью-Йорке. В течение 25 часов была парализована жизнь Нью-Йорка. Ущерб от последствий этой аварии составил более 1 млрд. долларов [3].
Спустя 26 лет, 14 августа 2003 года в 16 часов 11 минут по местному времени из-за повреждения на линии Ниагара-Мохок без электричества осталась почти вся восточная часть Северной Америки, т.е. 50 млн. человек [4].
О каждой из перечисленных аварий можно сказать, что данная энергосистема потеряла живучесть.
Живучесть электроэнергетической системы (ЭЭС) зависит от ее структуры, конфигурации, надежности электрооборудования, средств релейной защиты и противоаварийной автоматики, а также от квалификации обслуживающего персонала, запаса устойчивости, резерва активной мощности и т.д.[6].
При эксплуатации ЭЭС наблюдается появление так называемых цепочечных аварий из-за последовательного отказа в срабатывании нескольких выключателей, через которые прошел сквозной аварийный ток.
Цепочечные аварии наблюдались в 25 ЭЭС и двух ОЭС бывшего СССР. За 5 лет было зафиксировано 75 цепочечных аварий. В 81% случаев цепочечные аварии происходит из-за повреждений в сети отказов в функционировании ряда защитных коммутационных аппаратов [7].
На цепочечные аварии приходится 90% народнохозяйственного ущерба [8].
Под глубиной цепочной аварии понимается уровень расстройства функционирования установок энергосистемы при авариях и нарушениях в работе [9].
Показателем живучести может служить частота появления системных цепочечных аварий с различной глубиной нарушения электроснабжения [8].

На современном этапе развития техники и технологии для оценки надежности схем систем электроснабжения (СЭС) широкое распространение получили элементные методы расчетов надежности. В этих методах предполагается, что СЭС состоит из отдельных самостоятельных (в смысле анализа надежности) элементов, исключаются из рассмотрения функциональные зависимости между параметрами отдельных элементов и устройств [10-14].
Рассматриваемая подстанция состоит из элементов: линии электропередачи, трансформаторы, выключатели, отделители, разъединители, шины.
Под узлами схемы будем понимать физические пункты СЭС, которые непосредственно связаны не менее чем с тремя направлениями передачи энергии, т.е. обычно это сборные шины или секции распределительных устройств и т. д. [12].
От надежности узлов нагрузки зависит бесперебойное снабжение потребителей электрической энергией. Поэтому задачи, связанные с разработкой методов оценки надежности узлов нагрузки с учетом надежности средств защиты являются весьма актуальными.

Разработать методику расчетов для оценки живучести и надежности трансформаторных подстанций 110/10 кВ, снабжающих электроэнергией потребителей промышленных предприятий.

Для достижения поставленной цели необходимо решить следующие задачи:

разработать математическую модель надежности системы отключения защитного коммутационного аппарата;
предложить методику составления «деревьев» событий, объясняющих причины аварийного отключения узлов нагрузки, а также схем «минимальных сечений»;

при вести пример расчета надежности схем подстанций 110/10 кВ, которые снабжают электроэнергией потребители промышленных предприятий.

На основе однородных марковских случайных процессов с дискретным числом состояний и непрерывным временем предложена математическая модель надежности системы отключения выключателя, который работает в динамическом режиме.

Предполагается, что отказ в срабатывании выключателя происходит при совпадении в пространстве и времени двух случайных событий: появление короткого замыкания (КЗ) в зоне действия рассматриваемой защиты; отказ в срабатывании системы отключения выключателя.

Представим изменение состояния защищаемой сети во времени в виде случайной функции η (t), которая может принимать два значения: «0» и «1».
Состояния: «0» - в защищаемой сети нет повреждений, которые могут приводить к КЗ; «1» - в защищаемой сети произошло КЗ.

Последовательность чередующихся интервалов времени между КЗ обозначим через , а длительность существования КЗ (длительность срабатываемого защитного коммутационного аппарата) – через .
Пусть величины не противоречат экспоненциальной функции распределения вероятностей:
а - распределению
Величина - средний интервал времени между КЗ защищаемой сети.
- среднее время существования тока КЗ (или среднее время срабатывания защитного коммутационного аппарата).
Величины и взаимно независимы.
Переходы из состояния «0» → «1» и из «1» → «0» происходят мгновенно без выдержки времени.
Изменение состояния защитного коммутационного аппарата запишем с помощью аналогичной функции , которая также может принимать два значения: «0» и «1». Состояние «0» означает, что система отключения защитного коммутационного аппарата находится в работоспособном состоянии («ждущий режим»). Состояние «1» - в системе отключения защитного коммутационного аппарата имеется повреждения. Последовательность чередующихся случайных интервалов времени: отражает работоспособное состояние системы отключения выключателя, а последовательность - не работоспособное.
Пусть все имеют одно и тоже распределение
все - распределение
Величины - средний интервал времени между отказами в срабатывании защищаемого коммутационного аппарата; - среднее время нахождения системы защищаемого коммутационного аппарата в необнаруженном отказавшем состоянии.
Величины и взаимно независимы.
Переходы из состояния «0» → «1» и из «1» → «0» происходят мгновенно без выдержки времени.
Отказ защитного коммутационного аппарата наступает в момент встречи процессов
и в состоянии «1», то есть когда защитный коммутационный аппарат из-за отказов в системы отключения не в состоянии отключить случайно появившейся в защитной зоне ток КЗ.
Отказ защитного коммутационного аппарата в срабатывании в этом описании наступает в момент встречи процессов и в состоянии «1», то есть когда = 1, и = 1.
В начальный момент времени будем считать, что = =0, то есть система отключения защитного коммутационного аппарата исправна и находится в режиме «ожидания», КЗ в защищаемой сети отсутствует.
Задача состоит в том, что зная параметры процессов и определить: среднее время до отказов в срабатывании выключателя; дисперсию до отказов; вероятность нахождения системы в каждом из I возможных состояний; вероятность безотказной работы защитного коммутационного аппарата в течении времени.
Для нахождения вероятности безотказной работы защитного коммутационного аппарата при учете «скрытых отказов» в его системе отключения, совокупность процессов и рассмотрим, как один регулярный марковский процесс с четырьмя дискретными состояниями и непрерывным временем.

Система в любой момент времени t может находится только в одном из конечного множества состояний (Рис.1)

Рис.1. Возможная реализация регулярного однородного марковского случайного процесса с дискретными состояниями и непрерывным временем.

где - в защищаемой сети отсутствует КЗ; система отключения защитного коммутационного аппарата исправна и находится в «ждущем» режиме;
- в защищаемой сети произошло КЗ; система отключения
защитного коммутационного аппарата исправна и готова отключить ток КЗ;
- в защищаемой сети КЗ отсутствует; система отключения
защитного коммутационного аппарата находится в отказавшем состоянии;
- в защищаемой сети произошло КЗ; система отключения
защитного коммутационного аппарата находится в отказавшем состоянии.
При случайном попадании системы в состояние происходит отказ коммутационного аппарата.
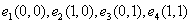- состояния системы;
и - регулярные однородные марковские случайные процессы;
, - время нахождения защищаемой сети в безотказном состоянии и время срабатывания защитного коммутационного аппарата соответственно;
, - время нахождения системы отключения защитного коммутационного аппарата в «ждущем» режиме и отказавшем состояниях соответственно.

Вероятность нахождения системы в каждом из четырех возможных состояний можно определит из системы уравнений:
Формула 1 (1)
Ввиду того, что
Формула 2 (2)

система линейных дифференциальных уравнений (1) примет вид:
Формула 3 (3)

Система уравнений (3) решается при начальных условиях:
которые вытекают из следующих предположений:
в защищаемой сети в данным момент времени отсутствуют КЗ, система защитного коммутационного аппарата находится в «ждущем» режиме.
Применяя к системе уравнений (3) прямое преобразование Лапласа и учитывая начальные условия, получим
Формула 4 (4)

Решая (4) относительно изображений искомых функций, после упрощений получим:
Формула 5 , (5)
Формула 6 , (6)

Формула 7 , (7)

где,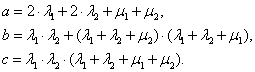
Вероятность безотказной работы защитного коммутационного аппарата при учете только отказов в срабатывании можно определить из выражения [17]:
Формула 8 (8)
где
Формула 9 (9)

где - символ обратного преобразования Лапласа.
Используя (5,6,7) и (9), получим
Формула 10                                                    (10)
Среднее время до первого отказа в срабатывании защитного коммутационного аппарата Формула 11 , и дисперсию находим из выражений [18]:
                                                                    (11)
Формула 12                                                     (12)

Используя (10,11,12), получим:

Формула 13                                                                    (13)
Формула 14                                                 (14)
Используя выражения (5,6,7) и применяя к ним обратное преобразование Лапласа, получаем:
Формула 15                                      (15)
Подставим в формулу (15) значения из (5,6,7):

Формула 16 (16)

Обозначим через:

Формула 17 (17)

Формула 18 (18)
Для получения обратного преобразования Лапласа используем формулу, приведенную в [19]:
Формула 19 (19)

где s- корни кубического уравнения.
В нашем случае корни кубического уравнения находим следующим образом [19]:

Формула 20 .                                                                       (20)
Подстановкой приводим кубическое уравнение (20) к «неполному» виду:
Формула 21 ,                                                                                                               (21)
где
Для описанной выше задачи Q<0 и Р<0, тогда корни кубического уравнения (21) определяются следующим образом:
Формула 22                                                    (22)
Подставляя значения корней в формулу (19, получим
Формула 23                                            (23)
Если система отключения защитного коммутационного аппарата проверяется через определенный интервал времени Θ и проверки абсолютно надежные, тогда можно определить из аналогичного выражения, полученного в [20]:
Формула 24 .                                                                        (24)
В том случае, если тогда:
Формула 25                                                                                            (25)
При выполнении условий
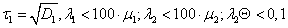Формула 26                                    (26)
формула для определения вероятности безотказной работы защитного коммутационного аппарата принимает вид:
Формула 27                                                                                    (27)
где
Формула 28                                                                                       (28)
где - параметр потока отказов в срабатывании защитного коммутационного аппарата.
Определим вероятность безотказной работы защитного коммутационного аппарата, пользуясь точной и приближенной формулами, при следующих исходных данных:
1/год - параметр потока ложных и излишних срабатываний РЗ;
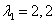1/год - параметр потока КЗ в зоне действия РЗ ЗКА;
1/год - параметр потока отказов в срабатывании системы отключения ЗКА;
год - интервал между проверками системы отключения ЗКА;
с - среднее время срабатывания системы отключения ЗКА;
год.
Используя данные примера и формулы (21)-(24) и (26) вычисляем точное значение для , а с помощью формулы (27) приближенное значение и в интервале времени" width="33" height="18" />.
На рис. 2 приведены графические зависимости полученных фнкций, из которых видно, что разница между точными и приближенными значениями и в интервале времени

Рис. 2 - Графики функции вероятности безотказной работы, построенные по точной и приближенной Следовательно, в том случае, если условие (26) соблюдается, то вероятность безотказной работы с достаточной для практических расчетов точностью можно оценивать с помощью формулы (27).

«деревьев», которые объясняют причины аварийного отключения секции шин подстанции 110/10 кВ, схемы «минимальных сечений» и приведен пример расчета надежности подстанций.

1. Разработаны положения и допущения, которые позволяют отказ в срабатывании защитного коммутационного аппарата представить, как процесс совпадения в пространстве и времени двух регулярных однородных марковских процессов, имеющих различную частоту появления и длительность существования.
2. На основе теории регулярных однородных марковских процессов
предложена новая математическая модель надежности защитного коммутационного аппарата, которая учитывает в динамическом режиме отказ в срабатывании системы отключения (релейная защита, отключающий соленоид, привод выключателя), а также сроки диагностики Θ системы его отключения.
3. При выполнении условия (26) разница между точными и приближенными значениями и в интервале времени года не превышает 1%.
4. Предложена методика составления «деревьев» событий, с помощью которых объясняются причины аварийного отключения узлов нагрузки подстанции 110/10 кВ.
5 Предложена методика учета надежности реле минимального напряжения и влияния его работы на надежность узла нагрузки.

1. Марков С.О. Разброс элементов, составляющих боевую силу судов. Морской сборник, 1894, № 6. - 106 с.
2. Надежность схем энергетики. Терминология. М.: Наука, 1980.
3. Prevention of power failures Vol.
3. Studies of the task groups on the northeast power interruption. A report to the federal power commission. June 1967, 142 p.
4. Горохов К. Америке утроили темную. Комсомольская правда в Украине. 16 августа 2003 года.
5. Руденко Ю.Н., Ушаков И.А. Надежность систем энергетики. М.: Наука, 1986. – 176 с.
6. Китушин В.Д. Определение характеристик отказов системы при цепочечном развитии аварий. – Изв. АН СССР. Энергетика и транспорт, 1977, № 6. стр. 20-30.
7. Гук Ю.Б. Анализ надежности электроэнергетических установок – Л.: Энергоатомиздат, 1984. – 176 с.
8. Гук Ю.Б. Анализ надежности электроэнергетических установок – Л.: Энергоатомиздат, Ленинградское отделение, 1988. – 224 с.
9. Розанов М.Н. Надежность электроэнергетических систем – М.: Энергоатомиздат, 1984 - 176 с.
10. Рябинин И.А. Основы теории и расчета надежности судовых электроэнергетических систем.-2-е изд. - Л.: Судостроение, 1971.-456 с.
11. Нечипоренко В.И. Структурный анализ систем (эффективность и надежность). - М.: Сов. радио, 1977. - 216 с.
12. Фокин Ю.А., Харченко А.М. Расчет надежности систем электроснабжения. – Электричество, 1982, №8, с. 5-10.
13. Константинов Б.А., Лосев Э.А. Логико-аналитический метод расчета надежности восстанавливаемых систем электроснабжения. – Электричество, 1971, № 12, с. 21-25.
14. Белоусенко И.В., Ершов М.С., Ковалев А.П., Якимишина В.В., Шевченко О.А. О раcчете надежности систем электроснабжения газовых промыслов. – Электричество, 2004, №3, С. 23-28.
15. Синьчугов Ф.И. Основные положения расчета надежности электроэнергетических систем. – Электричество, 1980, № 4, с. 12-16.
16. Лосев Э.А. Отклик на статью Ф.И. Синьчугова. – Электричество, 1981, № 9, с. 72-73.
17. Сандлел Дж. Техника надежности систем. Перевод с английского – Наука, 1966. – 300 с.
18. Креденцер Б.П. Прогнозирование надежности систем с временной избыточностью. – К.: Наукова думка, 1978. – 240 с.
19. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986. – 554 с.
20. Ковалев А.П., Шевченко А.В., Белоусенко И.В. Оценка пожарной безопасности передвижных трансформаторных подстанций 110/35/6 кВ// Промышленная энергетика . – 1991 - № 6. с. 28-31

Факультет :

электротехнический факультет

Специальность :

электротехнические системы электропотребления

Тема выпускной работы :

«Оценка живучести подстанции 110/35/10 кВ, которая снабжает электроэнергией промышленные предприятия»

Руководитель :

проф., д.т.н. Ковалёв Александр Петрович
kovaliov_alex@ukr.net