На основі однорідних марківських випадкових процесів з дискретним числом станів і безперервним часом запропонована математична модель надійності системи відключення вимикача, який працює в динамічному режимі.

Передбачається, що відмова в спрацьовуванні вимикача відбувається при збігу у просторі та часі двох випадкових подій: поява короткого замикання (КЗ) в зоні дії даного захисту; відмова в спрацьовуванні системи відключення вимикача.

Представимо зміну стану мережі, що захищається, в часі у вигляді випадкової функції η (t), ), яка може набувати два значення: «0» і «1».
Стани:  «0» - в мережі, що захищається, немає пошкоджень, які можуть приводити до КЗ; «1» - в мережі, що захищається, сталося КЗ.

Послідовність інтервалів часу, що чергуються, між КЗ позначимо через, а тривалість існування КЗ (тривалість захисного комутаційного апарату, що спрацьовує) – через .

   - розподілу
Величина  - середній інтервал часу між КЗ мережі, що захищається.
  - середній час існування струму КЗ (або середній час спрацьовування захисного комутаційного апарату).

Величини і  взаємно незалежні
Переходи із стану «0» > «1» і з «1» > «0» відбуваються миттєво без витримки часу.
Зміну стану захисного комутаційного апарату запишемо за допомогою аналогічної функції , яка також може набувати два значення: «0» і «1». Стан «0» означає, що система відключення захисного комутаційного апарату знаходиться в працездатному стані («режим, що чекає»). Стан «1» - в системі відключення захисного комутаційного апарату є пошкодження. Послідовність випадкових інтервалів часу, що чергуються:   відображає працездатний стан системи відключення вимикача, а послідовність  - не працездатне.
Хай всі мають одне і теж розподіл
все  - розподіл
  Величини  - середній інтервал часу між відмовами в спрацьовуванні комутаційного апарату, що захищається;  - середній час знаходження системи комутаційного апарату, що захищається, в невиявленому стані, що відмовив.Величини   і  взаємно незалежні.
Переходи із стану «0» > «1» і з «1» > «0» відбуваються миттєво без витримки часу.
Відмова захисного комутаційного апарату настає у момент зустрічі процесів
  і  в змозі «1», тобто коли захисний комутаційний апарат із-за відмов в системи відключення не в змозі відключити такою, що випадково з'явилася в захисній зоні струм КЗ.
Відмова захисного комутаційного апарату в спрацьовуванні в цьому описі настає у момент зустрічі процесів  і  в змозі «1», тобто коли = 1, і = 1.
У початковий момент часу вважатимемо, що  = =0, тобто система відключення захисного комутаційного апарату справна і знаходиться в режимі «очікування», КЗ в мережі, що захищається, відсутній.
Завдання полягає в тому, що знаючи параметри процесів   і визначити: середній час до відмов в спрацьовуванні вимикача; дисперсію до відмов; вірогідність знаходження системи в кожному з I можливих станів; вірогідність безвідмовної роботи захисного комутаційного апарату в перебігу часу.
Для знаходження вірогідності безвідмовної роботи захисного комутаційного апарату при обліку «прихованих відмов» в його системі відключення, сукупність процесів  і  розгледимо, як один регулярний марківський процес з чотирма дискретними станами і безперервним часом.  
Система у будь-який момент часу t може знаходиться тільки в одному з кінцевої безлічі станів ( Рис.1)

Рис.1. Можлива реалізація регулярного однорідного марківського випадкового процесу з дискретними станами і безперервним часом.

де - в мережі, що захищається, відсутній КЗ; система відключення захисного комутаційного апарату справна і знаходиться в режимі, що «чекає»;
 - у захищаємій мережі сталося КЗ; система відключення захисного комутаційного апарату справна і готова відключити струм КЗ;
 - у захищаємій мережі КЗ відсутній; система відключення захисного комутаційного апарату знаходиться в стані, що відмовив;
 - у захищаємій мережі сталося КЗ; система відключення захисного комутаційного апарату знаходиться в стані, що відмовив.
При випадковому попаданні системи в стан відбувається відмова комутаційного апарату.
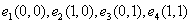- стани системи;
 i  - регулярні однорідні марківські випадкові процеси;
 ,   - час знаходження  захищаємої мережі в безвідмовному стані і час спрацьовування захисного комутаційного апарату відповідно;
 ,  - час знаходження системи відключення захисного комутаційного апарату в режимі, що «чекає», і що відмовив станах відповідно.
Вірогідність знаходження системи в кожному з чотирьох можливих станів можна визначить  з|із| системи рівнянь:
(1)
З огляду на те, що
                  (2)

 система лінійних диференціальних рівнянь (1) набере вигляду:
(3)

Система рівнянь (3) вирішується за початкових умов:
 які витікають з наступних припущень:
у мережі, що захищається, в даним момент часу відсутні КЗ, система захисного комутаційного апарату знаходиться в режимі, що «чекає».
Застосовуючи до системи рівнянь (3) пряме перетворення Лапласа і враховуючи початкові умови, отримаємо
(4)

Вирішуючи (4) щодо зображень шуканих функцій, після спрощень отримаємо:
,                   (5)
,         (6)

,                   (7)

де,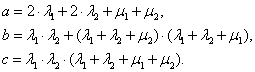
Вірогідність безвідмовної роботи захисного комутаційного апарату при обліку тільки відмов в спрацьовуванні можна визначити з рівняння [17]:
                      (8)
де
          (9)

де  - символ зворотного перетворення Лапласа.
Використовуючи (5,6,7) і (9), отримаємо
                   (10)
Середній час до першої відмови в спрацьовуванні захисного комутаційного апарату , і дисперсію  знаходимо з виразів [18]:
                                  (11)
                      (12)

Використовуючи (10,11,12), отримаємо:

         (13)
  (14)
Використовуючи вирази (5,6,7) і застосовуючи до них зворотне перетворення Лапласа, отримуємо:
(15)
Підставимо у формулу (15) значення   з (5,6,7):

  (16)

Позначимо через:

          (17)

   (18)
Для отримання зворотного перетворення Лапласа використовуваний форму­лу, приведену в [19]:
   (19)

де  - коріння кубічного рівняння.
У нашому випадку коріння кубічного рівняння знаходимо таким чином [19]:

.        (20)
Підстановкою  приводимо кубічне рівняння (20) до «неповного» вигляду:
,               (21)
де
Для описаного вище завдання Q<0 і Р<0, тоді коріння кубічного рівняння (21) визначається таким чином:
       (22)
Підставляючи значення коріння у формулу (19, здобудемо
        (23)
Якщо система відключення захисного комутаційного апарату перевіряється через певний інтервал часу І і перевірки абсолютно надійні, тоді  можна визначити з аналогічного вираження, отриманого в [20]:
.        (24)
В тому випадку, якщо 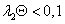 тоді:
      (25)
При виконанні умов
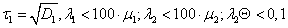   (26)
формула для визначення вірогідності безвідмовної роботи захисного ком¬утаційного апарату набуває вигляду:
             (27)
де      
    (28)
де
 - параметр потоку відмов в спрацьовуванні захисного комута­ційного апарату.
Визначимо вірогідність безвідмовної роботи захисного комутаційного апарату, користуючись точною і наближеною формулами, при наступних початкових даних:
 1/рік - параметр потоку помилкових і зайвих спрацьовувань РЗ;
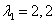 1/рік - параметр потоку КЗ в зоні дії РЗ ЗКА;
 1/рік - параметр потоку відмов в спрацьовуванні системи відключень ЗКА;;
 рік - інтервал між перевірками системи відключення ЗКА;
с - середній час спрацьовування системи відключення ЗКА
 рік.
Використовуючи дані прикладу і формули (21) -(24) і (26) обчислюємо точне значення для , а за допомогою формули (27) наближене значення.
На рис. 2 приведені графічні залежності отриманих фнкций, з яких видно, що різниця між точними і наближеними значеннями  і в інтервалі часу  рік не перевищує 1%.

Рисунок. 2 - Графіки функції вірогідність безвідмовної роботи, побудована по точній  і наближеній  формулах.
Отже, в тому випадку, якщо|у тому випадку , якщо умова (26) дотримується, то вірогідність безвідмовної роботи з достатньою для практичних розрахунків точністю можна оцінювати за допомогою формули (27).
В результаті розробки принцип побудови «дерев», які пояснюють причини аварійного відключення секції шин підстанції 110/10 кВ, схеми «мінімальних перетинів» і наведений приклад розрахунку надійності підстанцій.