


Струц Ольга Николаевна
Факультет электротехнический
Специальность: Электрические станции
Исследование математических методов решения электротехнических задач на ЭВМ
Научный руководитель: Сивокобыленко Виталий Федорович
Реферат по теме выпускной работы
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы
В настоящее время актуальной задачей является разработка математической модели электрической станции, позволяющей анализировать переходные процессы, возникающие при пуске, однофазных и многофазных коротких замыканиях [КЗ] на отходящих линиях электропередач, на сборных шинах, в трансформаторах и на их выводах, при обрывах фаз, а также при неполнофазных отключениях выключателей высокого напряжения. В настоящее время существуют такого типа модели, однако они позволяют рассчитывать эффективные значения токов и напряжений, тогда как для устройств релейной защиты и автоматики, а также для выбора оборудования требуются знания мгновенных значений параметров, указанных выше режимов.
На данный момент существует много способов составления и решения систем дифференциальных уравнений электрических станций, многие из них составлены с некоторыми допущениями, например явление вытеснения тока в пазу статора и ротора электрической машины учитывают с помощью двухконтурной схемы замещения, которая на данный момент наиболее точно отражает процессы, происходящие в электрической машине во время переходного процесса.
В зависимости от сложности электрической системы, исследуемого режима и ряда других факторов применяются два основных подхода при разработке математических моделей такого класса: с применением явных или неявных методов численного интегрирования. Вплоть до настоящего времени, в ранее разработанных методах [1,2] имеет место дилемма между получением необходимой точности расчета и сохранением при этом численной устойчивости и быстродействия. Поэтому вопрос поиска более совершенных алгоритмов расчета переходных режимов остается открытым, что особенно актуально для микропроцессорных терминалов, работающих в режиме РВ.
Применение неявных методов численного интегрирования дифференциальных уравнений(ДУ) является более перспективным, поскольку с их помощью возможно получить устойчивое решение при моделировании многократных коммутаций в электрических сетях любой сложности.
Цель работы
Целью работы является создание дискретной математической модели главной схемы электрических соединений электрической станции на основе полных дифференциальных уравнений. Для создания универсальной математической модели требуются полные математические описания всех элементов главной схемы.
Задачи исследования, поставленные в данной работе:
- выбор математических моделей и параметров основных элементов ЭС;
- разработка основного алгоритма расчета стационарных и переходных процессов;
- анализ поведения элементов главной схемы электрических соединений электростанций при возникновении и отключении симметричных и несимметричных КЗ различной длительности.
Методы исследования
Теоретические исследования базируются на основных положениях теории электротехники и режимов работы электростанций и систем, теории стационарных и переходных процессов машин переменного тока, численных методах анализа и вычислительной техники в системах электроснабжения.
Научная новизна полученных результатов:
1. Использование дискретных математических моделей синхронных машин, основанных на неявных методах численного интегрирования, что позволяет решить проблему возникновения численной неустойчивости при моделировании режимов работы электростанции;
2. Синтез параметров дискретных схем замещения электрических машин на основе каталожных данных;
3. Метод моделирования режимов коммутаций выключателей, основанный на использовании методов неявного интегрирования.
Математическая модель создана в среде MathCAD 2001.
Практическая ценность
Математическая модель, может иметь широкое практическое применение не только на электрических станциях, но и на любом предприятии, использующем большое количество асинхронных двигателей, бесперебойная работа которых должна обеспечивать безаварийное производство, что особенно важно для больших предприятий Донбасса.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Алгоритм расчета
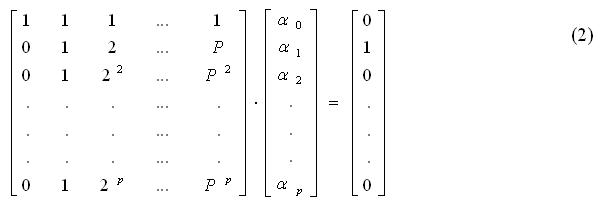
В основу численных методов, примененных в данной работе, будет положен многошаговый неявный метод, в котором осуществляют замену производных алгебраическим полиномом по формуле дифференцирования назад ФДН. Производная по (p+1) известному значению функции находится при этом как

Здесь 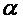 -постоянные коэффициенты, значения которых находят из уравнения (2), а S-количество предшествующих значений функции с интервалом между ними dx=h
-постоянные коэффициенты, значения которых находят из уравнения (2), а S-количество предшествующих значений функции с интервалом между ними dx=h
В частности, для метода второго порядка

Из ФДН могут быть получены также формулы численного дифференцирования функций по известным значениям функции в нескольких точках.
Для трех точек функции

Рассмотрим дискретную математическую модель для расчета ПП в электрической сети, в основе которой лежит метод ФДН. Вначале рассмотрим схему, состоящую из линейных двухполюсников с обобщенными параметрами и не содержащую источников тока.

Рисунок 1 - Схема замещения ветви электрической схемы с обобщенными параметрами
Обозначим напряжение на ветви  где U2 и U1 напряжения узлов начала и конца ветви соответственно. Матричное уравнение, описывающее состояние электрической цепи в момент времени t+h (h - шаг интегрирования), согласно закону Ома будет выглядеть следующим образом:
где U2 и U1 напряжения узлов начала и конца ветви соответственно. Матричное уравнение, описывающее состояние электрической цепи в момент времени t+h (h - шаг интегрирования), согласно закону Ома будет выглядеть следующим образом:
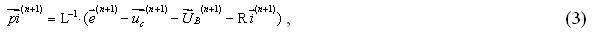
где R - матрица сопротивлений ветвей схемы, L - матрица собственных и взаимных индуктивностей ветвей;
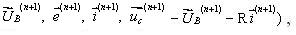 - вектора напряжений ветвей, ЭДС ветвей, токов ветвей и напряжений на емкостях ветвей соответственно (в момент времени t+h);
- вектора напряжений ветвей, ЭДС ветвей, токов ветвей и напряжений на емкостях ветвей соответственно (в момент времени t+h);
pi(n+1)- вектор производных токов ветвей по времени (в момент t+h);

Рисунок 2 - Дискретная схема замещения обобщенной ветви электрической схемы
Производную тока по времени pi(n+1) можно также рассчитать приближенным численным методом по двум и более точкам тока i(t). В качестве этих точек берем значения токов на текущем, следующем и нескольких предыдущих шагах интегрирования ДУ. Для обеспечения возможности изменения шага и порядка расчета воспользуемся общей формулой метода ФДН.
Приведем алгоритм расчета отдельно взятого шага переходного процесса, который будет аналогичен расчету установившегося режима:
1. Формируется матрица соединений схемы - П ( ПT ).
2. Формируются матрицы параметров схемы - R, L, и C. В случае нелинейных параметров матрицы рассчитываются по данным  или
или 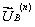
3. Определяется текущий шаг расчета h и порядок точности метода p.
4. Вычисляется вектор коэффициентов ФДН а, зависящий от h и p.
5. Рассчитываются матрицы дискретных сопротивлений и проводимостей
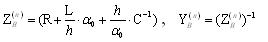
При обращении Z(n)B учитываем ее блочно-диагональную структуру
6. Вычисляем матрицу узловых проводимостей 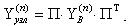
7. Обновляем вектор источников ЭДС схемы 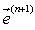 (t+h).
(t+h).
8. Рассчитывается вектор эквивалентных дискретных ЭДС:
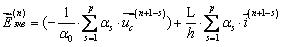
9. Находим узловое напряжение, решая систему линейных уравнений

При больших размерностях системы учитываем ее разреженность.
10. Находим вектора напряжений и токов ветвей

11. Находим вектор напряжений на емкостях

12. Сохраняем предыдущие значения векторов токов и напряжений на емкостях, необходимые для пунктов 8 и 11.
В общем случае, расчет по пунктам 2-12 выполняется в главном цикле моделирования переходного процесса. В случае постоянного шага и порядка пункты 3 и 4 выполняются один раз на первом шаге расчета с целью повышения производительности. Также при неизменных(линейных) R, L, и C, один раз выполняются пункты 2, 5 и 6.
Следует отметить, что вышеприведенный алгоритм позволяет моделировать коммутации простым скачкообразным изменением элементов матрицы R (или Z) в заданный момент времени.
С указанным подходом могут быть созданы макромодели АД, СД и других элементов.
В силовых цепях электрических систем параметры нелинейных элементов, таких как индуктивности с ферромагнитным сердечником (трансформаторы и электрические машины в режиме насыщения), изменяются в достаточно узких пределах. При учете электромеханических процессов также имеют место инерционные нелинейности в параметрах электрических машин. В связи с этим, для определения состояния электрической цепи в конкретный момент времени целесообразно воспользоваться линейной дискретной моделью, в которой параметры элементов на текущем шаге расчета будем считать постоянными. Для исключительных случаев, при появлении отклонений, предусмотрим выполнение 1-2 итераций для уточнения результата.
Дифференциальные уравнения элементов сети и их дискретные модели
Уравнения для элементов, обладающих пофазной симметрией (ЛЭП, трансформатор, кабель), будут записываться в трёхфазной системе координат a, b, c или в двухфазной системе х, y, то есть в неподвижной относительно статоров генераторов. Для симметричных электрических машин (асинхронные двигатели [АД]) используются оси х, y, а для несимметричных (синхронные генераторы и двигатели) - система координат, жёстко связанная с осями d, q ротора. При этом на каждом шаге расчёта для синхронных машин осуществляется пересчёт режимных параметров от осей d, q к осям всех остальных элементов a, b, c или х, y.
В моделях вращающихся электрических машин (двигатели и генераторы) используются схемы замещения с многоконтурным ротором, что позволяет более точно учитывать эффект вытеснения тока в роторе.
Для синхронных машин в связи с наличием на роторе обмотки возбуждения по продольной оси d ДУ целесообразно решать в осях d и q, жёстко связанных с его ротором (рис. 3). Только в этих координатах в уравнениях удаётся избежать периодических коэффициентов, зависящих от углового поворота ротора. Будем считать, что демпферный массив ротора по каждой оси представлен двухконтурной схемой замещения.

Рисунок 3 - Токи пуска синхронного двигателя в осях d и q
При известных параметрах схемы замещения, механической постоянной времени, реализуем программу расчета в пакете MathCAD для неявного метода Эйлера. Для асинхронного двигателя подобный расчет реализован неявным методом Эйлера (рис.4а) и ФДН 3го порядка для линейной дискретной модели (рис.4б).

Рисунок 4 - График скорости вращения при пуске АД
а) методом Эйлера
б) методом ФДН 3го порядкa
(анимация состоит из 5 кадров с задержкой в 50 мс между кадрами; количество циклов воспроизведения ограничено 5ю)
Также по известным каталожным данным, составим схему замещения и найдя ее параметры, можно найти токи стационарного и переходного процесса для остальных элементов схемы, например для трансформатора. Для него расчет будет вестись по упрощенной схеме, без учета ветвей намагничивания.
Здесь для нахождения значения потокосцепления используется численный метод - метод Рунге-Кутта. Для повышения производительности расчетов, а также сохранения устойчивости решений при коммутации в этой программе планируется заменить существующий метод на метод Эйлера, который позволяет получать пошаговые решения.
На данный момент существует программа ASDG-1 для моделирования переходных процессов в системе электроснабжения с асинхронными и синхронными машинами, в которой реализовано решение составление дифференциальных уравнений для отдельных элементов сети, составлены подпрограммы вычисления напряжений узловых и ветвей и расчета ДУ методом Рунге-Кутта.
ВЫВОДЫ
1. Разработаны дискретные схемы замещения основных элементов силовых электрических схем, основанные на неявных методах численного интегрирования ДУ и предназначенные для анализа переходных и аварийных режимов.
2. С использованием разработанных методов выполнен расчет переходного процесса в системе собственных нужд электрической станции, вызванного коротким замыканием и последующими действиями устройств релейной защиты и автоматики. Моделирование указанного режима при использовании известных методов выполнить затруднительно.
3. Ближайшей задачей является усовершенствование программы для возможности расчета системы с использованием дискретных методов.
ПЕРЕЧЕНЬ ПУБЛИКАЦИЙ И МАТЕРИАЛОВ ПО ТЕМЕ ВЫПУСКНОЙ РАБОТЫ
- Сивокобыленко В.Ф., Меженкова М.А. Поведение синхронных генераторов с системами самовозбуждения при близких коротких замыканиях // Сб. науч. трудов Донецкого гос. техн. унив-та. Серия: "Электротехника и энергетика". - Донецк: ДонГТУ. - 1998. - Вып. 2. - С. 20-23.
- Сивокобыленко В.Ф., Меженкова М.А. Расчет на ПЭВМ токов коротких замыканий для выбора уставок релейной защиты электростанций // Сб. науч. трудов Донецкого гос. техн. унив-та. Серия: "Электротехника и энергетика". - Донецк: ДонГТУ. - 1999. - Вып. 4. - C. 186-190.
- Сивокобыленко В.Ф., Меженкова М.А. Метод определения мгновенных значений симметричных составляющих токов и напряжений в переходных режимах// Вісник Нац. унів-ту "Львівська політехніка".- Львів: Львівська політехника. - 2000. - №403. - С. 149-156.
- Сивокобыленко В.Ф., Меженкова М.А. Определение параметров эквивалентных схем замещения турбогенераторов для расчетов на математических моделях // Зб. наук. праць Донецького держ. техн. унів-ту.. Серія "Електротехніка і енергетика". - Донецьк: ДонДТУ. - 2000. - Вип. 17. - С. 38-41.
- Сивокобыленко В.Ф., Меженкова М.А. Математическое моделирование электромеханических переходных процессов на электрических станциях // Электричество. - 2001. - №4. - С.5-9.
- Сивокобыленко В.Ф., Меженкова М.А. Математическая модель электрической станции для анализа поведения турбогенераторов с системами самовозбуждения при коротких замыканиях // Технічна електродинаміка. Cпец. випуск за матеріалами II Міжнародної науково-технічної конференції "Математичне моделювання в електротехніці та електроенергетиці". - Київ: Інститут електродинаміки НАН України. - 1998. - C. 100-105.
- Сивокобыленко В.Ф., Меженкова М.А. Разработка резервной защиты генераторов с системами самовозбуждения с помощью математической модели ТЭС // Книга за матеріалами п'ятої міжнар. науково-техн. конф. "Контроль і управління в складних системах" (КУСС-97). - Вінниця: УНІВЕРСУМ-Вінниця. - 1999. - Том 3. - C. 248-254.
- Сивокобыленко В.Ф., Меженкова М.А. Эквивалентные схемы замещения современных крупных турбогенераторов // ICEE-2000. Материалы IV Междунар. конф. "Электротехника, електромеханика и электротехнологии". - Россия, Москва, Клязьма, 18-22 сентября 2000.
- Сивокобыленко В.Ф., Меженкова М.А. Математическое моделирование симметричных составляющих токов и напряжений в переходных режимах// Тези доповідей 3-ї Міжнар. наук.-техн. конф. "Математичне моделювання в електротехніці, електроніці та електроенергетиці". - Львів. - 1999. - С. 242.
- Сивокобыленко В.Ф., Лебедев В.К. Переходные процессы в системах электроснабжения собственных нужд электростанций. Уч. пособие, Донецк, ДонНТУ, 2002. - 136 с.
- Перхач В.С. Математичні задачі електроенергетики. "Вища школа", Л. - 1989, 464 с.
[Вверх]