


Струц Ольга Миколаївна
Факультет електротехнічний
Спеціальність: Електричні станції
Дослідження математичних методів розв'язання електротехнічних задач на ЕОМ
Науковий керівник: Сивокобиленко Віталій Федорович
Реферат за темою выпускної роботи
ЗАГАЛЬНА ХАРАКТЕРИСТИКА РОБОТИ
Актуальність теми
У даний час актуальною задачею є розробка математичної моделі електричної станції, що дозволяє аналізувати перехідні процеси, які виникають при пуску, однофазних та багатофазних коротких замикань [КЗ] на на лініях електропередач, що відходять, на збірних шинах, у трансформаторах та на їх виводах, при обривах фаз, а також при неповнофазних відключеннях вимикачів высокої напруги. В даний час існують моделі такого типу, однак вони дозволяють розраховувати ефективні значення токів та напруг, у той час, як для пристроїв релейного захисту та автоматики, а також для вибору устаткування потрібні миттєві значення параметрів режимів, що вказані вище.
На даний момент існує багато засобов складання та розв'язання систем диференційних рівнянь електричних станцій, багато з них складені з деякими припущеннями, наприклад явище вытіснення току в пазу статора та ротора електричної машини враховують за допомогою двухконтурної схеми заміщення, яка на даний момент найбільш точно відображає процеси, що відбуваються в електричній машині під час перехідного процесу.
У залежності від складності електрічної системі, режиму, що досліджується та ряду інших факторів застосовуються два основні підходи при розробці математичних моделей такого класу: із застосуванням явних або неявних методів чисельної інтеграції. Аж до теперішнього часу, в раніше розроблених методах [1,2] має місце дилема між здобуттям необхідної точності розрахунку і збереженням при цьому чисельної стійкості і швидкодії. Тому питання пошуку досконаліших алгоритмів розрахунку перехідних режимів залишається відкритим, що особливо актуально для мікропроцесорних терміналів, що працюють в режимі РЧ.
Вживання неявних методів чисельної інтеграції диференціальних рівнянь(ДУ) є перспективнішим, оскільки з їх допомогою можливо отримати стійке рішення при моделюванні багатократних комутацій в електричних мережах будь-якої складності.
Мета роботи
Метою роботи є створення дискретної математичної моделі головної схеми електричних з'єднань електричної станції на основі повних диференціальних рівнянь. Для створення універсальної математичної моделі потрібні повні математичні описи всіх елементів головної схеми.
Завдання дослідження, поставлені в даній роботі:
- вибір математичних моделей і параметрів основних елементів ЕС;
- розробка основного алгоритму розрахунку стаціонарних і перехідних процесів;
- аналіз поведінки елементів головної схеми електричних з'єднань електростанцій при виникненні і відключенні симетричних і несиметричних КЗ різної тривалості.
Методи дослідження
Теоретичні дослідження базуються на основних положеннях теорії електротехніки і режимів роботи електростанцій і систем, теорії стаціонарних і перехідних процесів машин змінного струму, чисельних методах аналізу і обчислювальної техніки в системах електропостачання.
Наукова новизна отриманих результатів:
1. Використання дискретних математичних моделей синхронних машин, заснованих на неявних методах чисельної інтеграції, що дозволяє вирішити проблему виникнення чисельної нестійкості при моделюванні режимів роботи електростанції;
2. Синтез параметрів дискретних схем заміщення електричних машин на основі каталожних даних;
3. Метод моделювання режимів комутацій вимикачів, заснований на використанні методів неявної інтеграції.
Математична модель створена в середовищі MathCAD 2001.
Практична цінність
Математична модель, може мати широке практичне вживання не лише на електричних станціях, але і на будь-якому підприємстві, що використовує велику кількість асинхронних двигунів, безперебійна робота яких повинна забезпечувати безаварійне виробництво, що особливо важливе для великих підприємств Донбасу.
ОСНОВНИЙ ЗМІСТ РОБОТИ
Алгоритм розрахунку
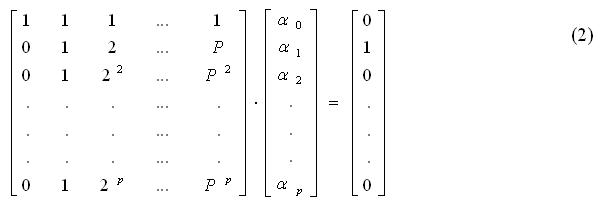
В основу чисельних методів, застосованих в даній роботі, буде покладено багатокроковий неявний метод, в якому здійснюють заміну похідних алгебраїчним поліномом за формулою диференціювання назад ФДН. Похідна по (p+1) відомому значенню функції знаходиться при цьому як

Тут 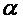 - постійні коефіцієнти, значення яких знаходять з рівняння (2), а S-кількість попередніх значень функції з інтервалом між ними dx=h
- постійні коефіцієнти, значення яких знаходять з рівняння (2), а S-кількість попередніх значень функції з інтервалом між ними dx=h
Зокрема, для методу другого порядку

З ФДН можуть бути отримані також формули чисельного диференціювання функцій по відомих значеннях функції в декількох точках
Для трьох точок функції

Розглянемо дискретну математичну модель для розрахунку ПП в електричній мережі, в основі якої лежить метод ФДН. Спочатку розглянемо схему, що складається з лінійних двополюсників з узагальненими параметрами і що не містить джерел струму.

Рисунок 1 - Схема заміщення гілки електричної схеми з узагальненими параметрами
Позначимо напругу на гілці  де U2 та U1- напруга вузлів початку і кінця гілки відповідно. Матричне рівняння, що описує стан електричного ланцюга у момент часу t+h (h - шаг интегрування), згідно із законом Ома виглядатиме таким чином:
де U2 та U1- напруга вузлів початку і кінця гілки відповідно. Матричне рівняння, що описує стан електричного ланцюга у момент часу t+h (h - шаг интегрування), згідно із законом Ома виглядатиме таким чином:
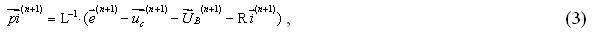
де R - матриця опорів гілок схеми, L - матриця власних і взаємних індуктівностей гілок;
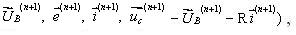 - вектора напруги гілок, ЕДС гілок, струмів гілок і напруги на ємкостях гілок відповідно (у момент часу t+h);
- вектора напруги гілок, ЕДС гілок, струмів гілок і напруги на ємкостях гілок відповідно (у момент часу t+h);
pi(n+1)- вектор похідних струмів гілок за часом (у момент t+h);

Рисунок 2 - Дискретна схема заміщення узагальненої гілки електричної схеми
Похідну струму за часом pi(n+1) можна також розрахувати наближеним чисельним методом по двох і більш точкам струму i(t). За ці точки беремо значення струмів на поточному, наступному і декількох попередніх кроках інтеграції ДУ. Для забезпечення можливості зміни кроку і порядку розрахунку скористаємося загальною формулою методу ФДН. Приведемо алгоритм розрахунку окремо взятого кроку перехідного процесу, який буде аналогічний розрахунку сталого режиму:
Приведем алгоритм расчета отдельно взятого шага переходного процесса, который будет аналогичен расчету установившегося режима:
1. Формується матриця з'єднань схеми - П ( ПT ).
2. Формуються матриці параметрів схеми - R, L, та C. У разі нелінійних параметрів матриці розраховуються за даними  або
або 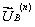 .
.
3. Визначається поточний крок розрахунку h і порядок точності методу h и порядок точності методу p.
4. Обчислюється вектор коефіцієнтів ФДН а, залежний від h та p.
5. Розраховуються матриці дискретних опорів і провідності:
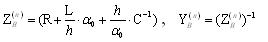
При зверненні Z(n)Bвраховуємо її блоково-діагональну структуру.
6. При Обчислюємо матрицю вузлових провідностей: 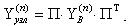
7. Оновлюємо вектор джерел ЕДС схеми 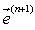 (t+h).
(t+h).
8. Розраховується вектор еквівалентних дискретних ЕДС:
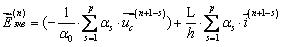
9. Знаходимо вузлову напругу, вирішуючи систему лінійних рівнянь:

При великій розмірності системи враховуємо її розрідженість.
10. Знаходимо вектора напруги і струмів гілок:

11. Знаходимо вектор напруги на ємностях .
.
12. Зберігаємо попередні значення векторів току та напруги на ємності, необхідні для пунктів 8 і 11.
У загальному випадку, розрахунок за пунктами 2-12 виконується в головному циклі моделювання перехідного процесу. У разі постійного кроку і порядку пункти 3 і 4 виконуються один раз на першому кроці розрахунку з метою підвищення продуктивності. Також при незмінних(лінійних) R, L, і C, один раз виконуються пункти 2, 5 і 6.
ССлід зазначити, що наведений вище алгоритм дозволяє моделювати комутації простою стрибкоподібною зміною елементів матриці R (або Z) в заданий момент часу.
Із вказаним підходом можуть бути створені макромоделі АД, СД і інших елементів.
Диференціальні рівняння елементів мережі і їх дискретні моделі
Рівняння для елементів, що володіють пофазной симетрією (ЛЕП, трансформатор, кабель), записуватимуться в трифазній системі координат а, b, с або в двофазній системі х, у, тобто в нерухомій відносно статорів генераторів. Для симетричних електричних машин (асинхронні двигуни [АД]) використовуються осі х, у, а для несиметричних (синхронні генератори і двигуни) - система координат, жорстко пов'язана з осями d, q ротора. При цьому на кожному кроці розрахунку для синхронних машин здійснюється перерахунок режимних параметрів від осей d, q до осей всіх останніх елементів а, b, с або х, у.
У моделях електричних машин (двигуни і генератори), що обертаються, використовуються схеми заміщення з багатоконтурним ротором, що дозволяє точніше враховувати ефект витіснення струму в роторі.
Для синхронних машин у зв'язку з наявністю на роторі обмотки збудження по подовжній осі d ДУ доцільно вирішувати в осях d і q, жорстко пов'язаних з його ротором (рис. 3). Лише у цих координатах в рівняннях удається уникнути періодичних коефіцієнтів, залежних від кутового повороту ротора. Вважатимемо, що демпферний масив ротора по кожній осі представлений двоконтурною схемою заміщення.

Рисунок 3 - Токи пуску синхронного двигуна в осях d і q
За відомих параметрів схеми заміщення, механічної постійної часу, реалізуємо програму розрахунку в пакеті MathCAD для неявного методу Ейлера. Для асинхронного двигуна подібний розрахунок реалізований неявним методом Ейлера (рис.4а) і ФДН 3го порядку для лінійної дискретної моделі (рис.4б).

Рисунок 4 - Графік швидкості обертання при пуску АД
а) методом Ейлера
б) методом ФДН 3го порядка
(анiмацiя складена з 5 кадрiв iз затримкою в 50 мс мiж кадрами; кiлькiсть циклiв повторення - 5)
Також за відомими каталожними даними, складемо схему заміщення і знайшовши її параметри, можна знайти струми стаціонарного і перехідного процесу для інших елементів схеми, наприклад для трансформатора. Для нього розрахунок вестиметься за спрощеною схемою, без врахування гілок намагнічення.
Тут для знаходження значення потокозціплення використовується чисельний метод - метод Рунге-Кутта. Для підвищення продуктивності розрахунків, а також збереження стійкості рішень при комутації в цій програмі планується замінити існуючий метод на метод Ейлера, який дозволяє отримувати покрокові рішення.
На даний момент існує програма ASDG-1 для моделювання перехідних процесів в системі електропостачання з асинхронними і синхронними машинами, в якій реалізовано рішення складання диференціальних рівнянь для окремих елементів мережі, складені підпрограми обчислення напруги вузлових і гілок і розрахунку ДУ методом Рунге-Кутта.
ВИСНОВКИ
1. Розроблені дискретні схеми заміщення основних елементів силових електричних схем, засновані на неявних методах чисельної інтеграції ДУ і призначені для аналізу перехідних і аварійних режимів.
2. З використанням розроблених методів виконаний розрахунок перехідного процесу в системі власних потреб електричної станції, викликаного коротким замиканням і подальшими діями пристроїв релейного захисту і автоматики. Моделювання вказаного режиму при використанні відомих методів виконати скрутно.
3. Найближчим завданням є удосконалення програми для можливості розрахунку системи з використанням дискретних методів.
ПЕРЕЛІК ПУБЛІКАЦІЙ І МАТЕРІАЛІВ ЗА ТЕМОЮ ВИПУСКНОЇ РОБОТИ
- Сивокобыленко В.Ф., Меженкова М.А. Поведение синхронных генераторов с системами самовозбуждения при близких коротких замыканиях // Сб. науч. трудов Донецкого гос. техн. унив-та. Серия: "Электротехника и энергетика". - Донецк: ДонГТУ. - 1998. - Вып. 2. - С. 20-23.
- Сивокобыленко В.Ф., Меженкова М.А. Расчет на ПЭВМ токов коротких замыканий для выбора уставок релейной защиты электростанций // Сб. науч. трудов Донецкого гос. техн. унив-та. Серия: "Электротехника и энергетика". - Донецк: ДонГТУ. - 1999. - Вып. 4. - C. 186-190.
- Сивокобыленко В.Ф., Меженкова М.А. Метод определения мгновенных значений симметричных составляющих токов и напряжений в переходных режимах// Вісник Нац. унів-ту "Львівська політехніка".- Львів: Львівська політехника. - 2000. - №403. - С. 149-156.
- Сивокобыленко В.Ф., Меженкова М.А. Определение параметров эквивалентных схем замещения турбогенераторов для расчетов на математических моделях // Зб. наук. праць Донецького держ. техн. унів-ту.. Серія "Електротехніка і енергетика". - Донецьк: ДонДТУ. - 2000. - Вип. 17. - С. 38-41.
- Сивокобыленко В.Ф., Меженкова М.А. Математическое моделирование электромеханических переходных процессов на электрических станциях // Электричество. - 2001. - №4. - С.5-9.
- Сивокобыленко В.Ф., Меженкова М.А. Математическая модель электрической станции для анализа поведения турбогенераторов с системами самовозбуждения при коротких замыканиях // Технічна електродинаміка. Cпец. випуск за матеріалами II Міжнародної науково-технічної конференції "Математичне моделювання в електротехніці та електроенергетиці". - Київ: Інститут електродинаміки НАН України. - 1998. - C. 100-105.
- Сивокобыленко В.Ф., Меженкова М.А. Разработка резервной защиты генераторов с системами самовозбуждения с помощью математической модели ТЭС // Книга за матеріалами п'ятої міжнар. науково-техн. конф. "Контроль і управління в складних системах" (КУСС-97). - Вінниця: УНІВЕРСУМ-Вінниця. - 1999. - Том 3. - C. 248-254.
- Сивокобыленко В.Ф., Меженкова М.А. Эквивалентные схемы замещения современных крупных турбогенераторов // ICEE-2000. Материалы IV Междунар. конф. "Электротехника, електромеханика и электротехнологии". - Россия, Москва, Клязьма, 18-22 сентября 2000.
- Сивокобыленко В.Ф., Меженкова М.А. Математическое моделирование симметричных составляющих токов и напряжений в переходных режимах// Тези доповідей 3-ї Міжнар. наук.-техн. конф. "Математичне моделювання в електротехніці, електроніці та електроенергетиці". - Львів. - 1999. - С. 242.
- Сивокобыленко В.Ф., Лебедев В.К. Переходные процессы в системах электроснабжения собственных нужд электростанций. Уч. пособие, Донецк, ДонНТУ, 2002. - 136 с.
- Перхач В.С. Математичні задачі електроенергетики. "Вища школа", Л. - 1989, 464 с.
[Нагору]