УПРАВЛЕНИЕ СКОРОСТЬЮ И МОМЕНТОМ ДВИГАТЕЛЕЙ С ПОПЕРЕЧНЫМ ПОТОКОМ ВОЗБУЖДЕНИЯ ОТ ПОСТОЯННЫХ МАГНИТОВ C ПРЯМОЙ ПЕРЕДАЧЕЙ В СЕРВОПРИВОДАХ
Вернер У., Шуттлер Й., Орлик Б.
Институт электропривода,силовой электроники и приборов
Источник:International power electronics and motion control conference, 11 - 14 September 2004, Dresden, Germany. EPE-PEMC 2005.
Ключевые слова
Регулируемый привод скорости, сервопривод, двигатель с постоянными магнитами, двигатель с поперечным потоком, моделирование, имитация
Реферат
Эта работа рассматривает инновационный метод минимизации момента зубцовых гармонических помех двигателей с поперечным потоком при прямом использовании сервоприводов, чтобы достигнуть точного регулирования скорости. Эти подходы основываются на расчете оптимальных диаграмм тока для реализации регулирования момента как основы для регулирования скорости.
Введение
На протяжении нескольких лет существует устойчивая тенденция к решениям привода с прямой передачей. Прямые передачи часто осуществляют с высокомоментными двигателями, которые, как правило, представлены медленновращающимися машинами. Они развивают очень высокий момент на низкой скорости. Следовательно, зубчатая передача может быть исключена; это увеличивает общий уровень эффективности и динамические свойства системы привода. Цель этой технологии – увеличить плотность момента ( ) или также весовую плотность момента ( ) в зависимости от нагрузки (мощность, скорость). Чтобы управлять непосредственно спаренной системой двигатель – нагрузка, скорость двигателя должна точно регулироваться. Чтобы реализовать точный контроль требуется постоянный момент двигателя в широком диапазоне скорости. Эта статья представляет как момент зубцовых гармонических помех двигателя с поперечным потоком (ДПП) может быть минимизирован оптимальным регулированием тока, для достижения требуемого регулирования скорости.
Двигатель с поперечным потоком
Двигатель с поперечным потоком представляет собой одну из топологий электрических машин с высокими силовыми плотностями. Исполнение этих электрических машин представляет существенное новшество в использовании прямых приводов. Выполнение требований по малым размерам и массе двигателей с высокой плотностью момента на низких скоростях играет важную роль. Концепция машин с поперечным потоком была развита в начале 20 века. Но из-за нехватки соответствующих электронных устройств и преобразователей практическое использование этих типов машин началось только несколько десятилетий назад. В 80-х гг. профессор Вех из технического университета Брунсвика, как один из пионеров в этой области, разработал новый тип машин основанный на принципе поперечного потока. Эти машины использовались как нерегулируемые тяговые силовые приводы. На сегодняшний день наличие интеллектуальных преобразователей энергии позволяет расширить использование машин с поперечным потоком для применений там, где необходимо регулирование скорости и колебаний энергии.
Типичный признак машин с поперечным потоком – наличие цепи магнитного потока, которая имеет секции, где поток поперечен плоскости вращения и обмотке в статоре, в которой направление тока аналогично направлению движения ротора. Инновационный дизайн цепи потока комбинированный с использованием новых магнитных материалов привёл к очень высококачественным машинам с плотностью рассеиваемой мощности в 3 – 5 раз больше по сравнению с аналогичными машинами постоянного тока, синхронной и индукционной. Это метод по которому машина с поперечным потоком с такой же номинальной мощностью меньше в размере и весе по сравнению с аналогичными машинами. Дополнительное преимущество ДПП – их повышенный КПД. Есть две главных причины для этого: пониженные потери в обмотке, благодаря отсутствию лобовых частей в обмотке статора и тот факт, что магнитная цепь и электрическая цепь не занимают одно и тоже пространство. Мы должны различать две различные топологии двигателей с поперечным потоком возбуждаемым постоянным электромагнитом (ДППМ). Одна топология – потококонцентрированый ДПП, а другая топология – плоский магнит ДПП. ДПП в конфигурации концентрации потока может достигать высокой степени плотности, но и имеет также высокую амплитуду колебаний момента. Конфигурация плоского магнита имеет пониженную степень плотности, но зависит от поверхности навесных магнитов, меньшие колебания моментов.

Рис.1 - Двухфазный ДППМ в потококонцентрированной конфигурации
На сегодняшний день действенной плотностью нормального асинхронного двигателя может достигать до 20-30 кН/м?. Водяное охлаждение и действенная плотность оптимизированной высокоэффективной машиной может достигать 65 кН/м? и на короткое время до 80 кН/м?. Норма для синхронной машины выполнять 40-60 кН/м?. Реактивные машины с поперечным потоком могут достигать 60 кН/м? и водяное охлаждение машины с постоянными магнитами и поперечным потоком дают более чем 200 кН/м?.
Кроме описанных преимуществ есть несколько недостатков у машин с поперечным потоком. Наличие скачков в диаграмме момента, колебание контактного давления, низкий коэффициент мощности и комплексный дизайн ядра. Колебания момента и колебание контактного давления производят шум и вибрации. Некоторые виды решений по уменьшению колебаний момента и колебания контактного давления. Один из них – модификация геометрии магнитной цепи. Кроме того, подходящая форма волны тока может быть использована в машине.
В этой статье введены передовые методы, в которых постоянный момент может быть получен оптимизируемой формой волны тока в машине с поперечным потоком. Необходимое регулирование тока для ДПП будет выполнено в микроконтроллере и протестировано на стенде с 3-х фазным ДПП с конфигурацией концентрации потока и 3-х фазные ДПП с конфигурацией плоских магнитов. Все описываемые методы и регулируемые структуры могут быть применены обеими типами машин.
Рис.2: Двухфазный ДППМ в конфигурации плоский магнит, эскиз по Ландерту
Вычисление оптимальной формы волны тока
Основан на том принципе, что ДПП имеет силовые точки без момента. Расстояние этих нулевых точек одно полюсное деление. Поэтому минимум двух фаз должен быть использован в ДПП с постоянными магнитами, чтобы компенсировать эти точки без момента. Моменты обеих фаз прикладываются к валу двигателя. Получение беззубцового момента обеих фаз связаны с девяностоградусным смещением тока, а также требуется специальная форма тока.
Как получить эти формы волн описано ниже. Очень простой и интуитивный метод [5] минимизации зубцовых моментов 2-х фазногоДПП – метод трапеций. Главный принцип этого метода основан на формировании трапециидальной форме волны тока, которая имеет цикл одного полюсного деления и которая меньше, чем максимально возможный момент (рис.3).
Нет нужды выбирать кривую с максимальным значением (как показано в примере). Используя аналитическую модель (описанную в [5]), возможно рассчитать соответствующий ток в фазе для каждой позиции ротора в порядке достижения необходимой формы колебаний момента. Общий момент обеих фаз формирует зубцовую кривую на максимальное значение трапецоида.
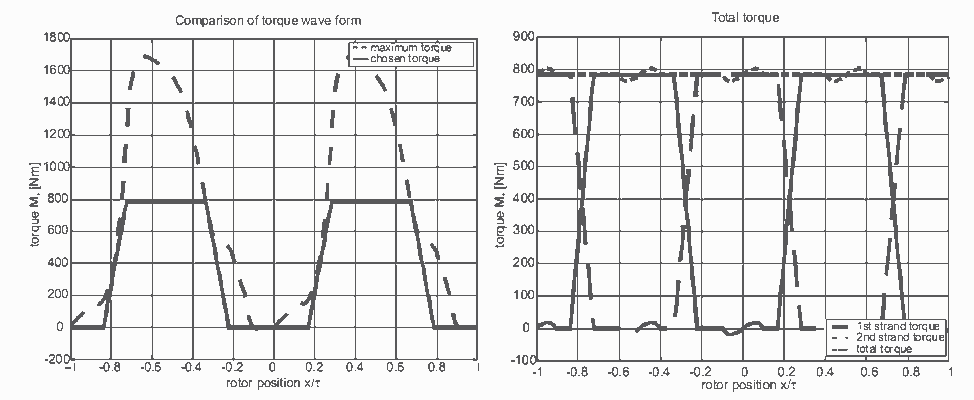
Fig.3 - Кривая трапецоида меньше,чем максимальный момент Fig.4 - Результат минимизации зубцовых моментов
Но есть две проблемы, как это показано на рис.3 и рис.4. Вокруг точки отсутствия момента при положении ротора х = 0 выбранная кривая не может быть осуществимой. Результирующая фактическая форма сигнала влияет на форму сигнала общего момента на том же положении. Для этого положение ротора простое табличное приближение производит очень высокое значение тока в этой части.
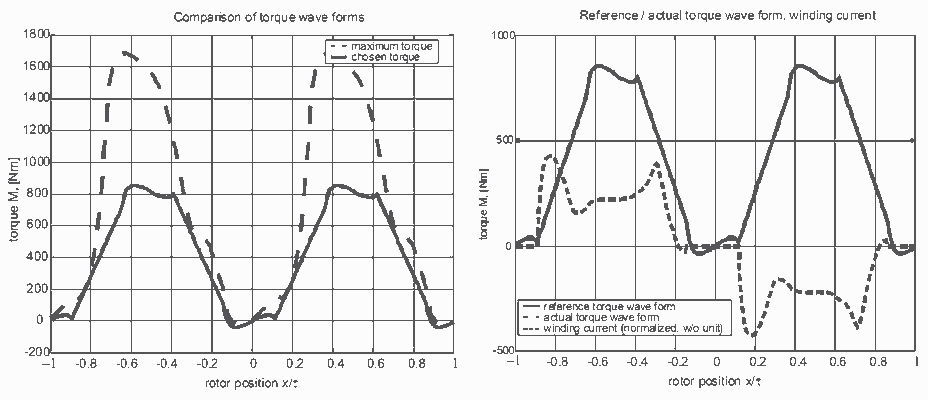
Рис.5 - Измененная кривая трапецоида; Рис. 6 - Реализация вычисленной кривой ммента
Простое изменение метода трапецоида устраняет обе проблемы. Вблизи точки отсутствия момента нулевой ток обязателен, как следствие форма сигнала момента индуктируется постоянными магнитами. В некоторой точке процесс генерации тока должен быть повёрнут назад от этого сигнал момента формирует трапецоидную кривую момента. Эта точка выбрана в порядке избегания вхождения в результирующую кривую. Отклонение от настоящей трапеции может быть компенсировано со второй фазой. Результаты рис.5 и рис.6 может быть достигнуты применением изменённого простого метода к максимально возможному моменту. Возможно добиться беззубцового момента высокого уровня с изменённым методом трапеции. Используемые вычисления очень просты и делают возможным применить это в оперативной работе, например, в алгоритме отключения по ошибке. Это даёт надежду на установку характеристических кривых и правильное введение токовых обмоток.
Регулируемая структура
Главное требование прямого управления – постоянный момент и постоянная скорость в каждой операционной точке. Достигать необходимых условий для ДПП точного регулирования момента и скорости нужно на базе быстрого регулирования тока. Следовательно, ДПП с ПМ с пониженными колебаниями момента и тока могут быть использованы в прямом сервоприводе. Регулируемая структура основана на расчёте модели ДПП представлена на рис.7.
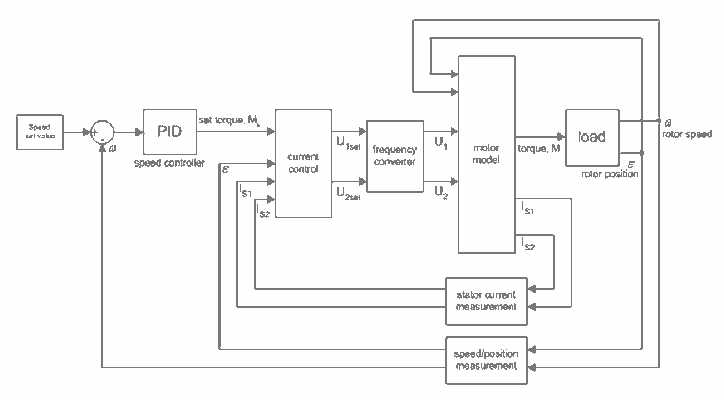
Рис.7 - Структура регулятора используемая в моделировании и микроконтроллере
. Кроме того, к этой структуре добавлено регулирование скорости. С вычисленной оптимизированной формой сигнала тока и регулируемой структурой минимального зубцового момента и скорости ожидается так как показано на рис.8 и рис.9.Поэтому, скорость и момент могут настраиваться точно в каждой операционной точке.
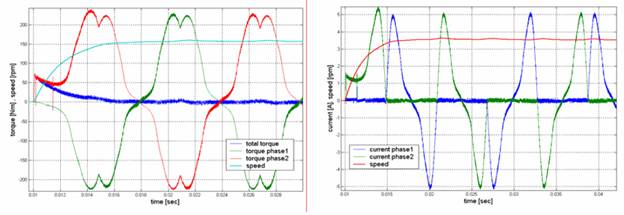
Рис.8 - Моделированный общий момент при номинальной скорости Рис.9 - Моделированный фазный ток и скорость
Проверка результатов моделирования регулируемой структуры выполняется в микроконтроллере и будет сделана разница тестов и измерений. Стенд с 3-х фазным ДПП описанный ниже изображён на рис.10. Нагрузка состоит из короткого вала с некоторой жёсткостью, элементами с низким коэффициентом трения и выключенной асинхронной машиной. Итак, контролер по существу работает с низким моментом инерции с низким коэффициентом трения.

Рис.10 - Тестовый стенд с трехфазным ДПП в конфигурации плоский магнит
Регулирование скорости в основном состоит из обычного ПИ- / ПИ- (регулятор тока) – контур, с добавлением компенсации по противо-ЭДС. Допустима почти совершенно пропорциональная взаимосвязь между током якоря и моментом вала, нелинейность насыщения, температура и зависимость положения ротора воспринимается контроллером как нарушение.
Всегда одна из трёх фаз токов/напряжений зависит от двух других, по методу законов Киргхофа, система может быть преобразована к двум независимым фазам преобразованием. Результат может быть выражен в Декартовой системе, в которой возможны векторные вычисления.
Для этого принципа векторного регулирования игнорируется асимметрия между тремя фазами. Структура на рис.10 не показывает уменьшение положения ротора ? только часть периода (электрический градус). Это предположение полностью игнорирует асимметрию при полном обороте. Итак, регулирование может только предоставлять желаемый результат для очень точного симметричного построения. Это веское непременное условие для трёхфазной машины, что очевидно в измерениях, приведённых выше.
Соответствующая область положения может быть получена из положения ротора, как это достоверно для синхронных машин, также вектор тока определяется максимальным моментом для небольшого смещения 90° (электрические градусы). Для однофазных режимов значение максимума тока при положении ротора в середине между полным полюсным перекрытием и положением между двумя соседними полюсами. Если абсолютное значение вектора тока остаётся неизменным, фазный ток во всех других положениях ротора принимает форму синусоиды.
Детальная структура регулирования изображена на рис.11.Толстые линии показывают количество векторов.
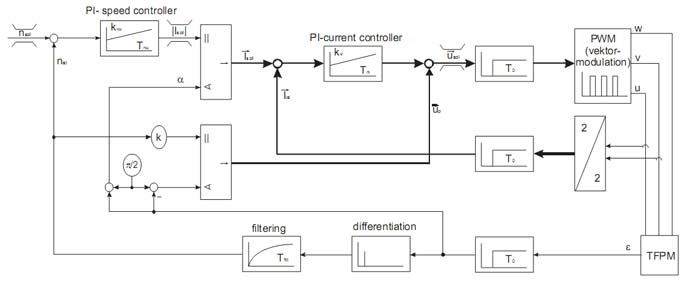
Рис.11 - Детализированная структура регулятора реализоапнная в микроконтроллере
Параметры регулятора были установлены kvw = 5 кгm и Tn = 15 mс, kvi = 40 и Tni = 5 mс средствами экспериментальной адаптации. Пропорциональный коэффициент k и угол обратного сдвига ЭДС определённый экспериментально. В контуре регулирования также некомпенсированная коммуникационная постоянная T0 = 187.5 mкc. Преобразователь включается между ±325 В постоянного тока на выходные клеммы. Фильтр в контуре скорости Tfilt регулируемый и был установлен для эксперимента на 500 mкc. Пределы были установлены nmax = 500 об/мин, |Imax| = 12 A, и |Vmax| = 216 В (фазное напряжение), каждый с механизмом противозависания для интегральных элементов контроллера. На рис.10 не показано условие безопасного отключения для натуральных значений и дополнительного ограничения для токовременной части для токов свыше 4А.
Измерения и результаты
Используя систему, описанную выше, была записана переходная характеристика скорости. Различные показания системы даны на рисунках с 12 по 16. Быстрый и стабильный режим регулирования показан в результатах. Заметно отсутствие компенсации зубцового момента в последней установившейся скорости, результаты с точностью 1,5%. Как результат некомпенсированной коммуникационной постоянной реальный вектор напряжения всегда содержит в себе отрицательный угол отклонения от желаемого вектора напряжения. Сравнение между фактическим и заданным значениями якорного тока – данные стационарной ошибки регулирования. Но это не влияет на режим регулирования скорости.
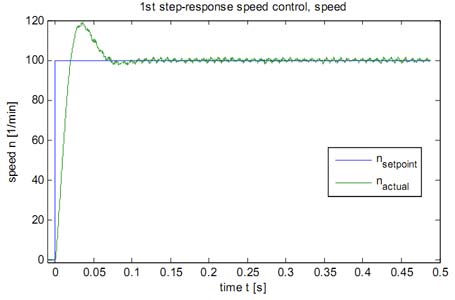
Рис.12 - Реакция на скачок регулятора скорости
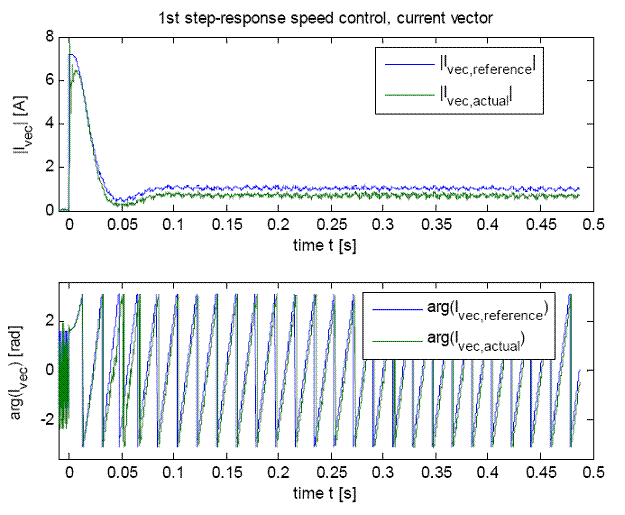
Рис.13 - Вектор тока и угол регулятора скорости
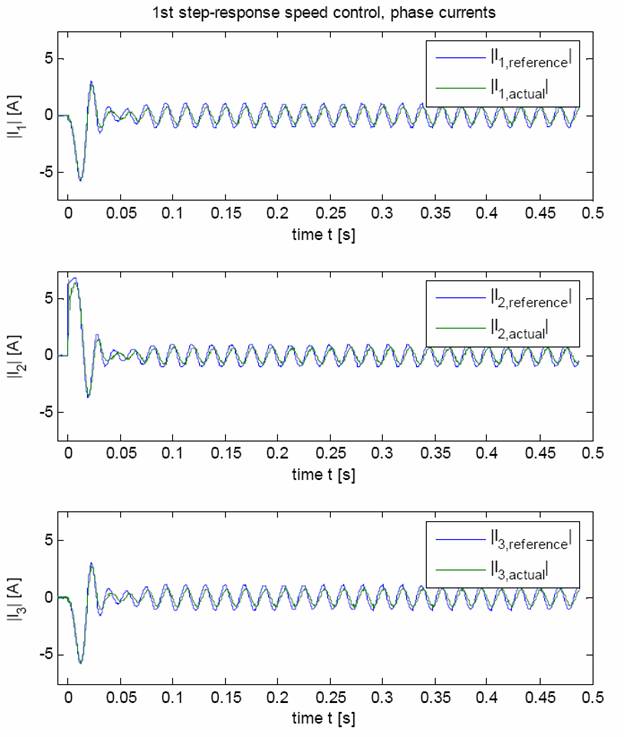
Рис.14 - Токи фаз
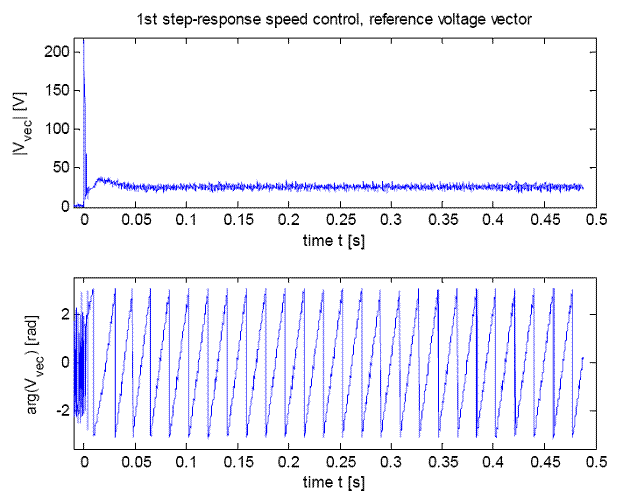
Рис.15 - Вектор напряжения
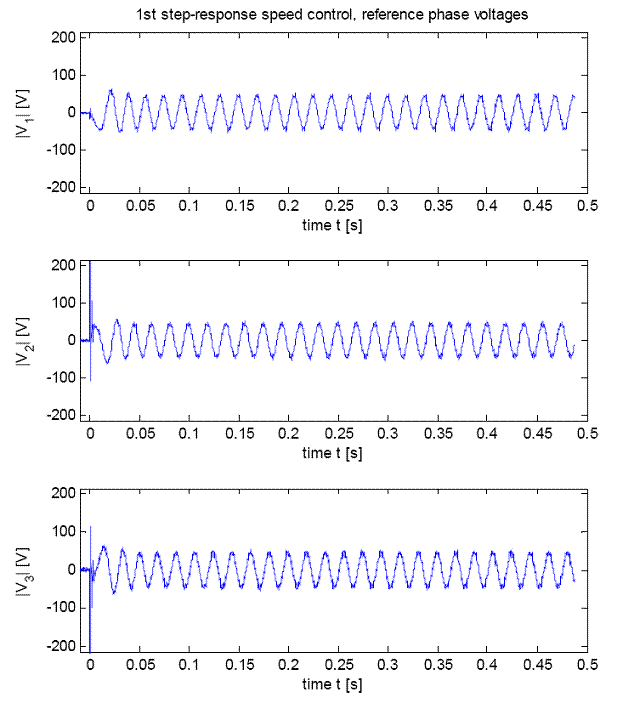
Рис.16 - Перенапряжение в трех фазах
Источники
[1] H. Weh, H. May: „Achievable force densities for permanent magnet excited machines in new configurations”, ICEM?86, Munich, 1986
[2] H. Weh: „Permanentmagneterregte Synchronmaschinen hoher Kraftdichte nach dem Transversalfluss-konzept“, etz Archiv, vol.10, pp.143-149, 1988
[3] U. Werner, H. Raffel, O. Harling, N. Parspour, B. Orlik: “Strategies to Reduce Torque and Current Ripples of Transverse Flux Permanent Magnet Generators for Wind Turbine Applications”. EPE, Toulouse/Frankreich 2003
[4] M. Vinogradski, U. Werner, B. Orlik: „Genetic Algorithms Used for Geometrical Structure Design of Transverse Flux Permanent Magnet Motors to Optimize the Torque Wave Form“. PCIM N?rnberg 2004
[5] M. Vinogradski, U. Werner, J.Schuttler, T. Petter, B. Orlik: „ Generation of optimized current wave forms for the production of minimized cogging torque of transverse flux motors for direct drive applications “. EPE-PEMC Riga/Latvia 2004
[6] Nurnberger I., Beineke S., Meyer N.: „Hohlwellen-Direktantriebe f?r Handlingaufgaben in Produktionsmaschinen“. Antriebstechnik Bd. 42 Nr.2, 2003
[7] http://www.servax.com/produkte/pdf/wm024/wm_024_d_high_torque.pdf
[8] http://www.servax.com/produkte/high_torque/mtc/massbilder/pdf/9_09_111b_massb_mtc1_145x.pdf
[9] S. Berchten: „Kosten sparen – mit Direktantrieben in Transversalflusstechnik“. Landert-Motoren AG, 8180 Bulach, Schweiz