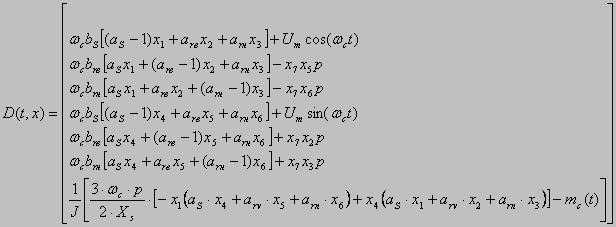Meznikova Katya

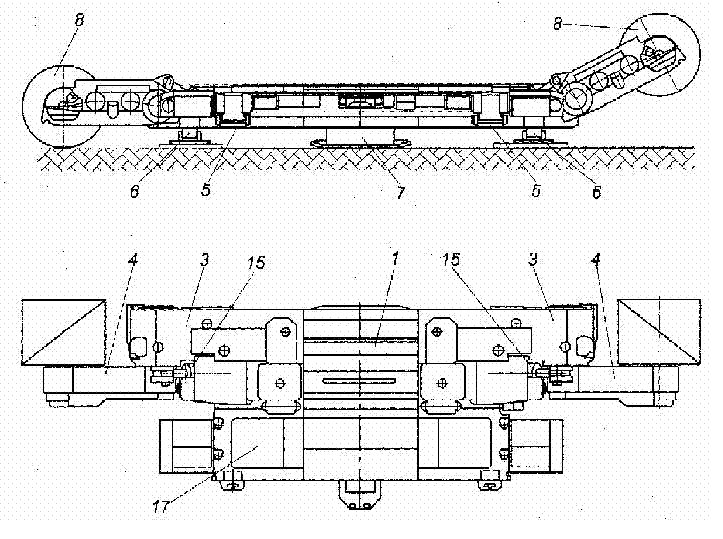
Object of research - the remote haulage system with frequency regulation of speed of a shearer UKD 200-250.

The purpose of work: To develop mathematical model for a substantiation of parameters of remote haulage system of shearer with the frequency converter.

INTRODUCTION

By extracting seam thickness of 0.8-1.2 m the question of coal quality improvement becomes a problem of today. Creation and introduction of highly – reliable shearers should provide improvement of coal quality. At the moment the shearer UKD 200-250 is the most actual for extraction of thin seam. Service factor of combines UKD 200-250 is 0.65, and service factor of other combines for thin seams does not exceed the level of 0.3. Combine UKD 200-250 is equipped with remote haulage system with chain hauling block. Parameters simulation and optimization of remote haulage system have the great practical importance as it is necessary to raise their speed characteristics and to expand an application field using a frequency - adjustable whim. Task of the given project is development of correct dynamic and mathematical models of working processes of remote haulage system with a frequency - adjustable whim

1 DEVELOPMENT OF MATHEMATICAL MODEL OF REMOTE HAULAGE SYSTEM WITH A FREQUENCY - ADJUSTABLE WHIM

Combine UKD 200-250 is intended for winning seams of 0-35 degrees with thickness of 0.85-1.3 m. The combine rests on the conveyor with four noncontrollable supporting mechanisms and on ground with one noncontrollable supporting mechanism. The combine has 1 electric motor for both whim effector subsystems and individual electric motors for subsystems of haulage.

The general view of a combine is presented in figure 2.

Figure 1 - Combine UKD 200-250

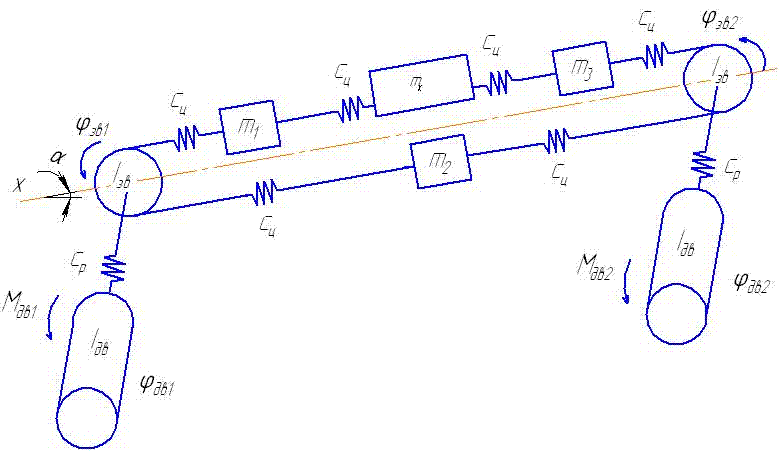
1 – the electric motor for whim effector subsystems;

3, 4 - the basic and ranging arm of whim effectors subsystems;

5, 6 – goaf and longwall supporting mechanisms;

7 - the supporting mechanisms on ground;

8 – effectors

15 - hydrojacks of a suspension mount and moving effector subsystems;

17 – a portal part of case-shaped subsystems.

To build a mathematical model of remote haulage system it is necessary to develop the dynamic circuit of a combine (fig. 2).

Figure 2 – The dynamic circuit of a combine

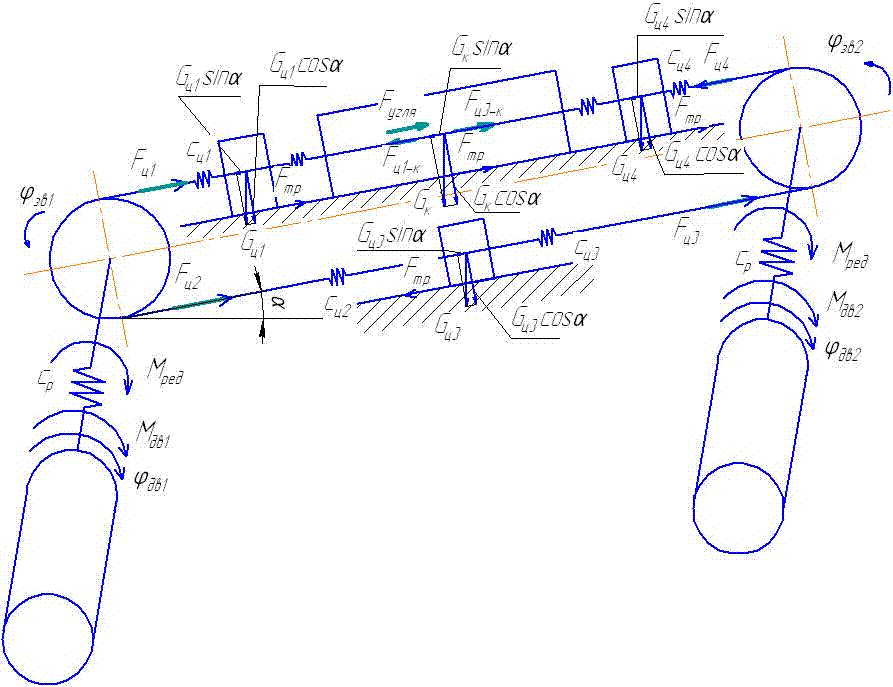
Let's specify the conventional signs:

Мдв1, Мдв2 – the leverage of the 1-st and 2-nd electric motors;

φдв1, φдв2 – rotational angles of rotors of 1-st and 2-nd electric motors;

Iдв1, Iдв2 – the moment of inertia of electric motors rotors;

Iзв – the moment of inertia of a drive chain sprocket;

Ср – factor of reducer rigidity of whim of remote haulage system;

βp – factor of reducer resistance;

Сц – factor of chain rigidity;

βц – factor of chain resistance;

φзв1, φзв2 – rotational angle of drive chain sprocket;

m1– mass of a hauling chain from drive chain sprocket 1 to combine;

m2 – mass of a hauling chain from drive chain sprocket 1 to drive chain sprocket 2;

m3 – mass of a hauling chain from drive chain sprocket 2 to combine.

Let's place forces which operate on a combine and chain links.

Figure 3 - Forces which operate on a combine and chain links

The mathematical model consists of the following cooperating modules:

- Mathematical model of the frequency - adjustable asynchronous electric motor;

- Mathematical model of remote haulage system which includes a whim, hauling unit and a shearer;

- Mathematical model of formation of resistance forces against a movement of a combine.

Mathematical model of the drive chain sprocket 1:

Mathematical model of the drive chain sprocket 2:

Model of a combine:

Model of the engine:

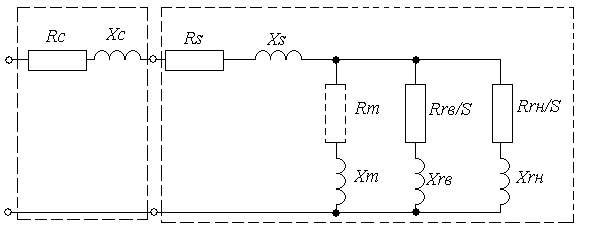
The mathematical model of the asynchronous engine is developed on the basis of researches of Parkа-Goreva.

Figure 4 - Substitutional connection of a phase of the asynchronous electric motor with the dual-circuit included in a mine network rotor

R_s, X_s - active and inductive resistance of a phase of a stator winding;

R_rв, R_rн - active resistance of phases of the top and bottom cages of a rotor, respectively;

X_rв, X_rн - inductive resistance of dispersion of the top and bottom cages of a rotor, respectively;

R_m, X_m - and inductive resistance of mutual induction;

R_c, X_c - and inductive resistance of a power line.

Design factors:

b_s, b_rв, b_rн - factors of relative resistance;

a_s, a_rв, a_rн - factors of relative reactance.

The basic equations MM [3]:

φ_р, ω_р - rotational angle and angular rate of rotor rotation;

J - the inertia moment of a rotor of the engine;

M_д - the electromagnetic moment of the engine;

M_с - the moment of loading on a motor shaft;

ψ_Sα, ψ_Sβ, ψ_нα, ψ_нβ, ψ_вα, ψ_вβ - components of linkage vectors;

ω_с - angular rate of a magnetic field;

t - current time;

ΔU_Sα, ΔU_Sβ - vector projections of a power failure of stator on an axis α and β in a view of a power line influence;

i_Sα, i_Sβ - currents of stator in a projection on axes α and β;

U_m - amplitude of a voltage in a phase;

U_н - rated voltage of a network (linear);

р - number of pairs poles of the electric motor;

Р_д - the active capacity consumed by the electric motor.

In a general view the system looks like:

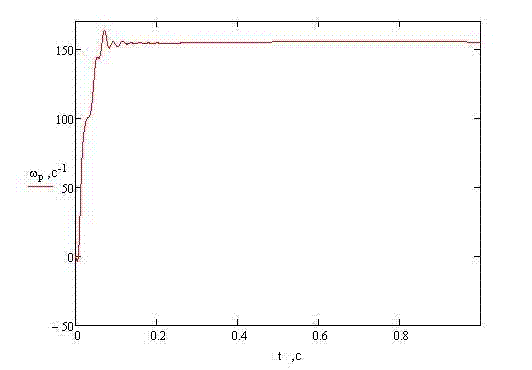
2 MODELLING OF AN ENGINE START-UP

With the help of program Mathcad it is necessary to simulate process of asynchronous engine running.

Let’s set the catalogue data, such as efficiency and the moment of inertia:

Крd=0.92

J=1.23

and parameters of an equivalent circuit - active and inductive resistance of a phase of a winding stator, inductive resistance of mutual induction, active and inductive resistance of the top and bottom cages of a rotor:

R_s=0.052
R_rv=0.079
R_rn=0.271
X_s=0.209
X_m=6.248
X_rv=0.557
X_rn=0.151

Torque:

m₀=1500
m_v=500
ω=6.28
m_c(t) = m₀+m_v·sin(ω·t)

Set entry conditions and calculate parameters of the right parts of the differential equation:

b_s=X_s^-1·R_s
b_rv=X_rv^-1·R_rv
b_rn=X_rn^-1·R_rn
X_sr=(X_m^-1+X_s^-1+X_rv^-1+X_rn^-1)^-1
a_s=X_s^-1·X_sr
a_rv=X_rv^-1·X_sr
a_rn=X_rn^-1·X_sr
p=2
ω_c=314
U_m=931

Calculation of the right parts of differential equation: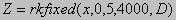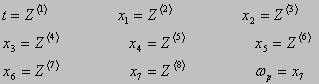

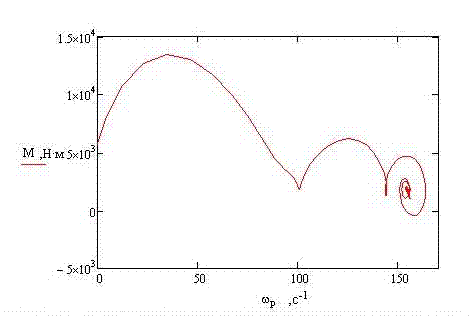
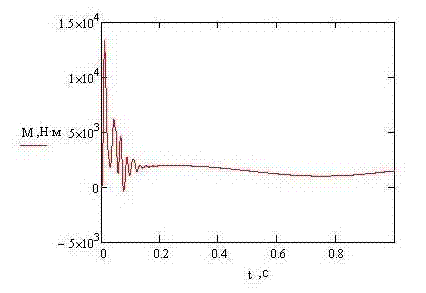
Figure 5 - Graphic dependence of the engine moment on rotor angular rate

Figure 6 - Graphic dependence of rotor angular rate on time

Figure 7 - Graphic dependence of engine moment on time

THE CONCLUSION

In the given project the mathematical model for a substantiation of parameters of remote haulage system of shearer with the frequency converter has been developed. By the instrumentality of the program Mathcad process of work of the asynchronous engine run is simulated.

REFERENCES

1. Решение научно-технических проблем при создании и внедрении современного горно-шахтного оборудования. Сборник научных трудов ГП «Донгипроуглемаш» /Науч.ред. В.В. Косарев, Н.И. Стадник. - Донецк: Астро, 2008. - 800 с.

2. Семенченко А.К., Кравченко В.М., Шабаєв О.Є. Теоретичні основи аналізу і синтезу гірничих машин і процесу їх відновлення, як динамічних систем /А.К.Семенченко, В.М.Кравченко, О.Є.Шабаєв – Донецьк: РВА ДонНТУ, 2002. – 302 с.

3. Миничев В.И. Угледобывающие комбайны. Конструирование и расчёт /В.И.Миничев - М.: «Машиностроение», 1976. - 248 с.

4. Оптимизация привода выемочных и проходческих машин /Под ред. чл.-кор. АН СССР А.В.Докукина - М.: Недра, 1983. - 264 с.

5. Горбатов П.А. Гірничі машини для підземного видобудування вугілля: Навч.посіб. для вузів /П.А. Горбатов, Г.В. Петрушкін, М.М. Лисенко, С.В. Павленко, В.В. Косарев; Під заг.ред. П.А. Горбатова. 2-ге вид.перероб. і доп. - Донецьк: Норд Комп'ютер, 2006. - 669с.:іл.

6. Горбатов П.А., Петрушкин Г.В., Лысенко Н.М. Горные машины и оборудование /П.А.Горбатов, Г.В.Петрушкин, Н.М.Лысенко: Учебное пособие для вузов - в 2-х т. Т.1. - Донецк: РИА ДонНТУ, 2003. - 295 с.

7. Горбатов П.А., Петрушкин Г.В., Лысенко Н.М. Горные машины и оборудование /П.А.Горбатов, Г.В.Петрушкин, Н.М.Лысенко: Учебное пособие для вузов - в 2-х т. Т.2. - Донецк: РИА ДонНТУ, 2003. - 201 с.

8. Гетопанов В.Н., Гудилин Н.С., Чугреев Л.И. Горные транспортные машины и комплексы /В.Н.Гетопанов, Н.С.Гудилин, Л.И.Чугреев: Учебник для вузов. - М.:Недра, 1991. - 304 с.

9. Малевич Н.А. Горнопроходческие машины и комплексы /Н.А. Малевич: Учебник для вузов. - М.:Недра, 1980. - 384с.

10. Хорин В.Н. Техника для выемки тонких пластов /В.Н.Хорин - М.:Недра, 1984. - 216 с.

11. Бойко Н.Г. Динамика очистных комбайнов. - Донецк: РВА ДонНТУ, 2004. - 206 с.

12. Кондрахин В.П., Гуляев В.Г., Головин В.Л. Имитационная математическая модель динамических процессов очистных комбайнов высокой энерговооружённости с вынесенной системой подачи. - Наукові праці Донецького національного технічного університету, вип.113, Серія: гірничо-електромеханічна, Донецьк, 2006. С.123-130.

13. Дубинин С.В., Сидоренко И.Т. Переходные процессы в системе подачи угольных комбайнов с электромагнитными муфтами скольжения. Известия вузов. Горный журнал. 1987. - С.88-93.

14. Подцепаев В.В.Математическая модель вынесенного привода подачи комбайнов для тонких пластов //Научн.тр.ИГД им. А.А.Скочинского. - 1983. - Вып.218. - С.56-62.

Now master's degree work is in a state of development. Complete its ending is planned on at end December, 2009.

To the beginning of page