| Автобиография |
| Автореферат |
| Ссылки |
| Отчет о поиске |
| Электронная библиотека |
| Индивидуальное задание |
| ДонНТУ Портал магистров ДонНТУ |
О ТОЧНЫХ РЕШЕНИЯХ ЗАДАЧИ О ВРАЩЕНИИ ТВЁРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
|
|
| Источник: Збірник статей міжвузівської студентської науково-технічної конференції «Механіка та сучасна техніка», ДонНТУ, м. Донецьк, 2 червня 2009 р. | |
|
Движение твёрдого тела в общем случае можно рассматривать как сумму двух движений: поступательного движения, определяемого движением какой-либо выбранной точки тела, и вращения вокруг этой точки. В качестве точки, вместе с которой рассматривается поступательное движение, выбирают центр масс тела, т.к. его движение описывается известной теоремой о движении центра масс механической системы. К изучению движения тела вокруг центра масс можно применить общие положения о вращении твёрдого тела вокруг неподвижной точки, поэтому задача о движении тела около неподвижной точки имеет важное значение в механике твёрдого тела [1]. Твёрдое тело с одной неподвижной точкой имеет три степени свободы, следовательно, положение твёрдого тела в любой момент времени можно определить тремя независимыми обобщёнными координатами. Классическими обобщёнными координатами являются углы Эйлера: φ – угол собственного вращения, ψ – угол прецессии, θ – угол нутации (рис.1).
Кинематические уравнения Эйлера имеют вид:
где ωx, ωy, ωz - проекции угловой скорости ω вращения тела вокруг неподвижной точки 0 на подвижные оси координат, связанные с телом. Начиная с 1758 г., когда Л.Эйлер опубликовал свои динамические уравнения движения тела с одной неподвижной точкой
не прекращаются попытки построения решений системы уравнений (1) – (2). В классической постановке, когда рассматривается одно твёрдое тело в однородном силовом поле, известны три первых интеграла и интегрирующий множитель системы дифференциальных уравнений Эйлера, и для полного аналитического решения достаточно найти лишь один (четвёртый) интеграл. Таким образом, задача представляется очень близкой к окончательному решению. Кроме того, интерес к этой задаче вызывает и то, что при движении тела вокруг неподвижной точки возникают эффекты, получившие название гироскопических, которые широко используются в технике. Однако, несмотря на усилия учёных всего мира, общее решение этой задачи до сих пор не найдено, за что её называют «математической русалкой». Следует заметить, что за двухсотлетний период (с 1758 г. до 1959 г.) было построено лишь 12 частных решений. Открытие каждого из них, при отсутствии общего метода зависело от искусства исследователя и в значительной мере носило случайный характер. В середине прошлого века Н.Е.Жуковский обобщил постановку Л. Эйлера на систему тел, состоящую из тела-носителя и несомых масс, совершающих по отношению к нему циклические движения. Такая система получила название гиростата. В дифференциальные уравнения (2) вошёл гиростатический момент λ, и динамические уравнения движения гиростата записываются в виде:
Почти все результаты, полученные ранее для одного твёрдого тела, к настоящему времени обобщены на гиростат. В созданной П.В.Харламовым Донецкой школе механиков было разработано несколько научных направлений, основанных на соответствующих фундаментальных результатах, и развитых затем учёными Донецка. Благодаря методу инвариантных соотношений П.В.Харламовым был предложен чёткий алгоритм построения точных решений задач механики [2]. П.В.Харламов ввёл такие новые (специальные) оси координат [3], которые привели к возможности понижения порядка системы уравнений (3) для гиростата, находящегося в поле сил тяжести. Благодаря дальнейшим исследованиям Донецких учёных, стало возможным построение новых классов решений, как классической задачи, так и различных её обобщений. К настоящему времени найдено 22 решения, из которых 16 принадлежат Донецким учёным. В монографии [4] предложена классификация данных к тому времени решений по степени инвариантного соотношения. В монографии [5] приводится перечень всех найденных решений классической задачи о движении тяжёлого гиростата с неподвижной точкой с указанием ограничений, наложенных на параметры системы, при которых они были найдены. СПИСОК ИСТОЧНИКОВ
|
|
| ДонНТУ | Портал магистров ДонНТУ | Автобиография | Автореферат | Ссылки | Отчет о поиске | Электронная библиотека| Индивидуальное задание |

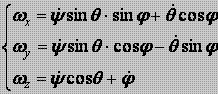 , (1)
, (1)
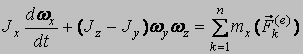 (123), (2)
(123), (2)
 (123), (3)
(123), (3)