Андрианова Ольга Сергеевна
Факультет: вычислительной техники и информатикиКафедра: компьютерных систем мониторинга
Специальность: компьютерный эколого-экономический мониторинг
Тема магистерской диссертации:
"Скрытая передача больших массивов информации путем стегокодирования WAV-файлов"
Научный руководитель: Губенко Наталья Евгеньевна, доцент, к.т.н.
Источник: http://www.contrterror.tsure.ru/site/magazine7/06-23-Fedorov-Makarevich-Rublev.htm
Е
В. М. Федоров, О. Б. Макаревич, Д. П.Рублев
Россия, г.Таганрог, Таганрогский государственный
радиотехнический университет
МЕТОД СТЕГАНОГРАФИИ В АУДИОСИГНАЛАХ И
ИЗОБРАЖЕНИЯХ, УСТОЙЧИВЫЙ К КОМПРЕССИИ С ПОТЕРЯМИ
В последние годы в связи с широким распространением сетевых средств передачи мультимедийной информации, в частности, голосового трафика и видеопотоков актуальным является построение на их основе потоковых стегосистем. Однако, применение стегосистем, использующих модификацию наименее значимых бит (НЗБ) исходных мультимедиа-данных ограничивается тем, что передача практически всех потоков мультимедиа-данных ведётся с применением того или иного метода сжатия, зачастую основанного на психофизиологической модели восприятия человека. В частности если рассматривать оцифрованную речь как один из наиболее распространённых источников мультимедиа-трафика, то в зависимости от области применения используется либо один из вариантов дифференциальной модуляции либо специализированные речевые кодеки. Использование множества НЗБ методов стеганографии в таком случае оказывается неэффективным и особую значимость приобретают методы стеганографии, позволяющие производить встраивание сообщений в перцептивно значимые области, которые не подвергаются существенных искажениям при обработке современными кодеками.
Анализ литературы показывает практически полное отсутствие методов встраивания устойчивых к компрессии мультимедийных данных. Одним из преобразований, позволяющих осуществить подобное встраивание, является дискретное вейвлет-преобразование [1]. Как известно, набор вейвлетов, в их временном или частотном представлении, может приближать сложный сигнал или изображение, причем как идеально точно, так и с некоторой погрешностью. Вейвлеты имеют явные преимущества в представлении локальных особенностей функций и неявном учёте особенностей психофизиологической модели восприятия. Благодаря этому они широко используются для анализа особенностей, сжатия и реконструкции сложных сигналов.
Покажем, что их применение при разработке метода стеганографии, ориентированного на достижение максимальной пропускной способности (скрытая передача и хранение информации) можно решить основные задачи стеганографии [2], а именно: минимизация вносимых искажений и устойчивость к атакам пассивного злоумышленника.
Вейвлеты – это обобщенное название временных функций, имеющих
вид волновых пакетов той или иной формы, локализованных по оси независимой
переменной (t или x) и
способных к сдвигу по ней или масштабированию (сжатию-растяжению). Вейвлеты
создаются с помощью специальных базисных
функций – прототипов, задающих их вид и свойства. По локализации во
временной и частотной областях они занимают
промежуточное положение между синусоидальной функцией и функцией Дирака
[3].
Практика работа с вейвлетами обычно базируется на
особой трактовке вейвлет-преобразований в частотной области и позволяет
плодотворно использовать хорошо разработанный и давно известный аппарат частотной
фильтрации и методы быстрого вейвлет-преобразования. Они основаны на
пирамидальном алгоритме Маллата и прореживании спектра вейвлетов по частоте
[3].
Рассмотрим частотный подход. В соответствии с этим подходом частотная область вейвлетов может быть разбита на две составляющие – низкочастотную и высокочастотную. Их частота раздела равна половине частоты дискретизации сигнала. Для их разделения достаточно использовать два фильтра – низкочастотный Loи высокочастотный Hi, к входам которых подключается сигнал . Фильтр дает частотный образ для аппроксимации (грубого приближения) сигнала, а фильтр для его детализации.
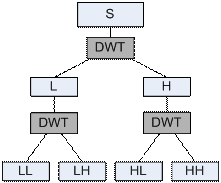
Поскольку фильтры передают только половину всех частотных компонент сигнала, то не попавшие в полосу прозрачности компоненты могут быть удалены. Эта операция называется операцией децимации вдвое. Если просто сложить полученные на выходах фильтров сигналы, то получится исходный сигнал, то есть будет иметь место полная реконструкция сигнала на начальном уровне. Однако Lo-фильтр можно, в свою очередь, разложить на два фильтра и подвергнуть спектры этих новых фильтров операции прореживания по частоте – децимации. Это означает изменение уровня реконструкции. Таким образом, может быть сформирована система вейвлет-фильтров, реализующих операцию декомпозиции сигнала того или иного уровня (см. рис. 1).
Подобные операции сокращают спектр соответствующих компонентов сигнала, что лежит в основе приближенного представления сигнала на разных уровнях декомпозиции. Такое представление необходимо, например, для реализации операции сжатия и очистки от шумов. Операция последовательной разбивки Lo-фильтров и постепенного огрубления сигнала была предложена Маллатом и известна как алгоритм Маллата.
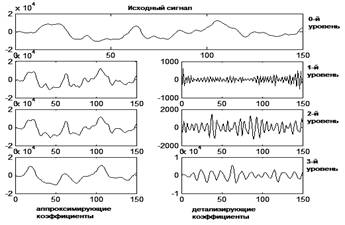
Рис. №1 — 3-х уровневая вейвлет-декомпозиция сигнала
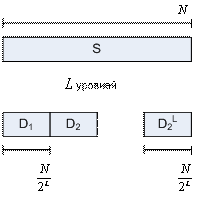
В предлагаемом методе областью встраивания является множество коэффициентов субполос декомпозиции. На первом этапе при помощи усовершенствованного алгоритма Маллата [3] производилась декомпозиция сигнала аудиофайла. Для этого нормированный сигнал аудиофайла подавался на фильтры декомпозиции низких и высоких частот, после чего с помощью операции децимации ↓2 (уменьшения числа частотных составляющих вдвое) находились коэффициенты аппроксимации и детализирующие коэффициенты на выходе фильтров на выходе низких и высоких частот (рисунок 2а). В результате декомпозиции на глубину L были получены коэффициенты субполос по N коэффициентов в полосе.
|
|
|
|
(а) |
(б) |
|
Рис. №2 — Декомпозиция при помощи усовершенствованного алгоритма Маллата на глубину 2 (а) и результат декомпозиции N отсчётов сигнала на глубину L (б) |
|
Восстановление сигнала производится заменой прямого дискретного вейвлет-преобразования на обратное и прохождением этапов декомпозиции в обратном порядке. Полученные в результате декомпозиции коэффициенты субполос являются пространством сокрытия информации.
Для установления минимально необходимой глубины разложения, при которой субъективные искажения качества практически не воспринимаются, были проведены эксперименты по встраиванию информации в частотные субполосы различных уровней с последующим восстановлением в аудиофайлы. В результате проведённых экспериментов было установлено, что искажения качества звука перестают восприниматься с глубины разложения L=4, при этом встраивание в высокочастотные субполосы практически не оказывает влияние на субъективное качество сигнала с глубины декомпозиции L=3. В качестве базисного вейвлета для встраивания использовались вейвлеты Добеши.
Для встраивания информации в коэффициенты может быть использовано множество различных способов. При необходимости скрытия информации без обеспечения стойкости к искажениям встраивание может производиться модулированием коэффициентов встраиваемой информационной последовательностью с ёмкостью 1 бит/коэффициент:
![]()
где wi— i-й коэффициент выбранной субполосы,
bi— символ информационной последовательности.
Восстановление информации осуществляется сравнением коэффициента с пороговой величиной thrsh
![]()
Таким образом, для
монофонического оцифрованного аудиосигнала частоты дискретизации Fs при встраивании
информации в окна коэффициентов длины
![]() при глубине
декомпозиции
l - пропускная способность
стеганографического канала:
при глубине
декомпозиции
l - пропускная способность
стеганографического канала:
![]()
Для сигнала частоты дискретизации 8 кГц при длительности 10 секунд и выборе глубины декомпозиции 4 с длиной окна l=1 пропускная способность стегоканала составит 500 бит/с на одну субполосу вейвлет-декомпозиции.
Извлечение информации осуществляется сравнением с пороговой величиной суммы модулей коэффициентов входящих в окно и записью результата в бинарной форме:

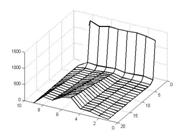
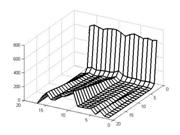
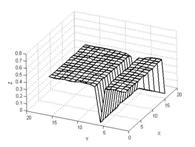
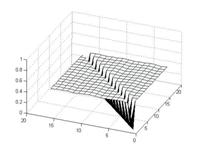
Усреднённая оценка битовых ошибок при встраивании бита в два коэффициента приведена на рисунках 3а-3б. Для усреднения были использованы результаты 30 экспериментов. В каждом из них генерировалась псевдослучайная бинарная последовательность, используемая в качестве сообщения.
Зависимость количества битовых ошибок от субполосы разложения и выбранного порога приведена на рисунке 3
На графиках субполос виден чёткий минимум количества битовых ошибок, который достигается одновременно для каждой из субполос при определённом значении коэффициента. Данное значение находится в зависимости от выбранной глубины декомпозиции и модуляции. В качестве оценки её математического ожидания можно выбрать медиану полученных сумм модулей и затем производить поиск экстремума производной отсортированных значений в окрестности.
|
|
|
|
(а) |
(б) |
|
Рис. № 3 — Зависимость количества битовых ошибок от субполосы разложения и выбранного порога для одного (а) и двух (б) коэффициентов на бит информации (по оси Z — логарифмическая шкала) |
|
При извлечении встроенных данных из блоков коэффициентов субполос аудиофайла полученная последовательность содержит битовые ошибки. Вероятность возникновения ошибок зависит, в первую очередь, от параметров звукового файла (частоты дискретизации, разрядности представления одного отсчёта). Полное подавление битовых ошибок возможно, но это требует введения итеративной процедуры оценивания, при которой после встраивания бита информации производится оценка корректности восстановления, а также стойкости к искажениям. При ошибке восстановления либо изменяются параметры алгоритма встраивания (глубина и вид модуляции) либо данный блок коэффициентов пропускается. Данный подход оптимален по критерию минимума энергии, но, вместе с тем, более сложен и применим не во всех случаях, в частности при работе в режиме реального времени, при ограничении на вычислительную сложность операций и.т.д. Проведённые исследования показали, что встраивание информации в коэффициенты субполос вейвлет-декомпозиции без последующего перевода сигнала в аналоговую форму само по себе обеспечивает достаточную стойкость к искажениям. Однако максимально полное восстановление информации возможно только при верно выбранном пороге обнаружения. Для определения пороговой величины по имеющемуся контейнеру была предложен следующий способ.
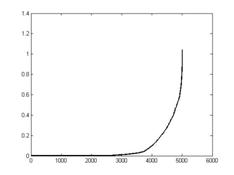
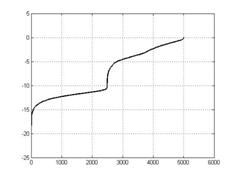
Последовательность
i=1..N, сумм коэффициентов
выбранной субполосы (рис. 4а) упорядочивается по возрастанию с формированием
последовательности c (рис. 4б). Для сжатия
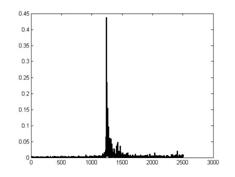
динамического диапазона значения логарифмируются (рисунок 4в) и далее находится
первая производная (рисунок 4г). При встраивании псевдослучайной
последовательности с равными вероятностями появления “
После
выделения центрального участка определяется индекс
![]() максимума и отрезок слева считается состоящим из сумм,
соответствующих нулевым битам исходной последовательности. В качестве оценки
уровня коэффициентов при передаче “
максимума и отрезок слева считается состоящим из сумм,
соответствующих нулевым битам исходной последовательности. В качестве оценки
уровня коэффициентов при передаче “![]() . Уровень пороговой величины определяется: thrsh=lev*a
. Уровень пороговой величины определяется: thrsh=lev*a
где полученное
эмпирически значение a=1.5.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
Рис. №4 — Этапы
определения величины
thres |
|
При оценке стойкости данного метода стеганографии к атакам активного злоумышленника одной из наиболее важных характеристик является возможность восстановления злоумышленником пространства преобразования, в котором была встроена информация. В данном случае представляет интерес возможность установления факта встраивания либо извлечение встроенной информации на основе другого базисного вейвлета. Для установления возможности осуществить обнаружение и извлечение информации без знания вейвлета, используемого при встраивании была проведена серия экспериментов. В качестве стеганографического контейнера для встраивания информации использовался аудиофайл с 10-ти секундной записью голоса диктора с частотой дискретизации 8кГц и разрядностью отсчёта 16 бит. Для исходного аудиофайла строилось полное дерево вейвлет-декомпозиции. Сообщение, представляющее собой псевдослучайную битовую последовательность было встроено в коэффициенты субполосы, выделенной при помощи дискретной вейвлет-декомпозиции на глубину L. В качестве базисного вейвлета для декомпозиции использовались вейвлеты Добеши. Встраивание битового потока производилось в выбранную субполосу прямой модуляцией коэффициентов с результирующей ёмкостью 1 бит/коэффициент. После встраивания из модифицированной субполосы, содержащей битовую последовательность и остальных субполос восстанавливался аудиосигнал и формировались выходные файлы. Таким образом, было сформировано 16 файлов, содержащих встроенную информацию на 4 уровне декомпозиции в одной из субполос. Далее производилась последовательная декомпозиция извлечённого из него сигнала на основе вейвлет-преобразований Добеши порядков от 1 до 20. Вероятности корректного извлечения бита сообщения в зависимости от порядка вейвлета Добеши и субполосы декомпозиции приведены на рисунке 5. Битовая последовательность была встроена с использованием вейвлета Добеши-6. Из приведённого рисунка видно, что применение при извлечении информации вейвлета, отличного от использованного на этапе встраивания, приводит к невозможности восстановления исходной битовой последовательности (вероятность правильного извлечения битовой позиции составляет 0.5). Минимум вероятности ошибки на графике (среднее значение 0.0119), соответствует значению вейвлета Добеши-6.
|
|
|
|
(а) |
(б) |
|
Рис. № 5 — Вероятность битовой ошибки при извлечения бита, скрытого на уровне 5 декомпозиции Добеши шестого порядка вейвлетами порядков 1-16 (а) и средняя вероятность битовой ошибки при рассмотрении вейвлетов Добеши порядков 1-20 |
|
При встраивании информации прямым изменением коэффициентов единственно информацией, неизвестной злоумышленнику является выбранный вейвлет. Помимо этого, при наличии в передаваемой последовательности длинных серий нулей и единиц способно привести к воспринимаемым на слух артефактам. Также передача одного из состояний бита не изменяет состояния канала— в коэффициент или окно коэффициентов изменения не вносятся и сохраняется их статистика в пределах окна, что теоретически допускает проведение стегоанализа на основе последовательностей наименее значимых бит. Для устранения данных недостатков авторами был предложены методы встраивания в последовательность коэффициентов не непосредственно битов сообщения, модулированных коэффициентами, а низкочастотного сигнала-паттерна. В качестве сигнала могут выступать синусоидальный низкочастотный сигнал, а также псевдослучайная последовательность. При этом параметры модулирующего сигнала (частота и фаза синусоиды, фрагмент псевдослучайной последовательности) являются ключом встраивания. Модифицированное встраивание имеет следующие преимущества:
1. Снижение искажений при встраивании. Существует возможность адаптивного подбора паттерна с учётом модели сигнала.
2. Повышение скрытности канала. Для извлечения информации злоумышленнику необходимо не только располагать вейвлетом, использованным на этапе скрытия, но также и сигналом-паттерном, по меньшей мере для одного из битовых символов.
3. Повышение стойкости к стегоанализу, так как из сигнала исключаются немодифицированные участки на основе которых возможно проведения статистического стегоанализа.
Слияние осуществляется в соответствии с выражением:
![]()
где
![]() — коэффициент выделенного окна после операции слияния,
— коэффициент выделенного окна после операции слияния,
wi— коэффициент выделенного окна до операции слияния,
![]() — отсчёт сигнала-паттерна, соответствующий встраиваемому в
текущее окно биту информации ,
— отсчёт сигнала-паттерна, соответствующий встраиваемому в
текущее окно биту информации ,
α— коэффициент ослабления исходной субполосы.
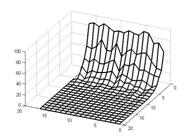
Наибольший интерес для сравнения методов встраивания представляют зависимость искажений контейнера и количество битовых ошибок в зависимости от коэффициента встраивания. При увеличении коэффициента a количество битовых ошибок уменьшается, но вместе с тем возрастают и искажения сигнала. Влияние переменного коэффициента a [0.01:0.2]на количество битовых ошибок субполос при глубине декомпозиции 3 и 4 приведено на рисунках 6(а-б). Увеличение глубины декомпозиции в данном случае не оказывает влияния на вероятность битовых ошибок.
|
|
|
|
(а) |
(б) |
|
Рис. №6 — Количество битовых ошибок (ось Z) при использовании переменного коэффициента a[0.01:0.2] (ось Y) для вейвлета Добеши-6 и глубине декомпозиции 3(а) и 4(б) |
|
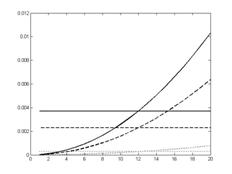
Важным критерием применимости того или иного стеганографического метода для сокрытия информации является величина вносимых методом искажений. При встраивании модулированного сигнала на фиксированном уровне разложения среднеквадратичное отклонение сигнала от исходного зависит от выбранного коэффициента a. На приведённых графиках (рисунок 7) коэффициент a изменялся с шагом 0.05. Величина среднеквадратичного отклонения монотонно возрастает с увеличением коэффициента и при значении a=0.61 отклонение становится равным отклонению при прямой модуляции битовой последовательностью.
|
|
|
|
Рис. № 7 — Изменение среднеквадратичного отклонения при встраивании модулированного сигнала с изменяющимся коэффициентом a[0.01:0.2] и прямым обнулением коэффициентов (горизонтальные линии) первых 3-х субполос |
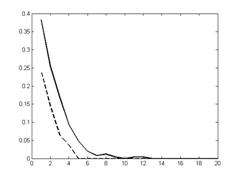
Рис. № 8 — Максимальное (сплошная линия) и минимальная (пунктирная линия) вероятности битовой ошибки при переменном коэффициенте a[0.01:0.2] |
Проведённые эксперименты показали, что предложенный метод позволяет сохранять встроенную информацию при конвертировании в формат файла. При оценке стойкости разработанных методов стеганографии к атакам пассивного злоумышленника одной из важных характеристик является оценка вероятности восстановления скрытого сообщения. В результате проведённых экспериментов было установлено, что извлечение информации в отсутствие сведений об использованном вейвлете невозможно. Это позволяет обеспечивать высокий уровень скрытности на основе конструирования вейвлетов, зависимых от ключа. При дальнейших исследованиях метода интерес представляют техники модуляции коэффициентов, обеспечивающие высокую пропускную способность при сохранении стойкости к искажениям, вносимых форматами компрессии с потерями, в частности, предлагаемый метод устойчив к преобразованию формата представления мультимедийных данных (квантование, компрессия с потерей качества). Метод также позволяет встраивать информацию в цифровые изображения.
Библиографическийсписок
1 P.Meerwald Digital image watermarking in the wavelet transform domain. Diplomarbeit zur Erlangung des Diplomgrades an der Naturwissenschaftlichen Fakultät der Universit
2 Генне О.В. Основные положения стеганографии //ООО “Конфидент” журнал “Защита информации. Конфидент”. – 2000. – №3. – С.20-24.
3 Дьяконов В., Матлаб. Обработка сигналов и изображений. Специальный справочник, - СПб.: Питер, 2002. 608 с.
Работа выполнена при поддержке гранта РФФИ 05-07-90372-в