Библиотека

Перевод тематической статьи

Метод критических путей – альтернатива моделирования неисправностей

M. Abramovici, P.R. Menon, D.T. Miller

Перевод: Довганич Е.В.

Краткий обзор

Мы представляем альтернативу моделирования неисправностей, направленную на метод критических путей (далее МКП), который определяет неисправности, обнаруженные при тестировании алгоритма обратной трассировки, который стартует от начальных выходов схемы. МКП является методом аппроксимации, но введение аппроксимаций встречается редко и не влияет на полезность метода. Этот метод есть более рациональным, чем обычное моделирование неисправностей.

1. Введение

Моделирование неисправностей выполняется в следующих приложениях:
• оценка теста путём определения его полноты (степени обнаружения неисправностей);
• создание словаря неисправностей;
• определение необнаруживаемых (несущественных) неисправностей с целью последующей генерации тестов;
• пост-тест диагностика (поиск неисправностей).

Существует три основных метода моделирования неисправностей, названные параллельным, дедуктивным и конкурентным методами. К тому же, два других метода оперируют только с комбинационными схемами и называются «распространение единичной неисправности» и метод Хонга. Комбинация этих двух способов использована в системе генерации тестов РОDEM-X. Специализированные методы для комбинационных схем широко используются при контроле-пригодном проектировании, таком как LSSD, которое преобразует последовательную схему в комбинационную с целью её тестирования. Даже для комбинационных схем, время, потраченное только на моделирование неисправностей, пропорционально n^2, где n – число выводов схемы. Увеличение количества выводов в VLSI-схемах требует более эффективных методов для оценки теста и его генерации.

В этой статье мы представляем альтернативу моделирования неисправностей, называемую МКП. Для определения обнаруживаемых неисправностей выполняется моделирование исправной схемы, в ходе которого рассчитываются значения сигналов для критических путей, сканируемых от первичных выходов (POs) и до первичных входов (PIs). По сравнению с обычным моделированием неисправностей, характерными особенностями МКП являются:
• непосредственно определяются обнаруживаемые неисправности некоторым тестом без моделирования всех возможных неисправностей. Следовательно, не требуется выполнение работы, касающейся распространения неисправностей, которые не обнаруживаются тестом, направленным на PОs;
• неисправностями оперируют только косвенно. Поэтому нам не требуется длительное перечисление неисправностей, их сокращение, распределение (для многопроходного моделирования), вставка и исключение неисправностей;
• нет необходимости в рассчёте значений на выходах неисправной схемы при логическом анализе и обработке списка неисправностей;
• метод является приближённым.

Следовательно, МКП работает быстрее и требует меньше памяти, чем обычное моделирование неисправностей. Аппроксимация происходит редко и заключается в немаркированном обнаружении некоторых неисправностей, которые фактически определяются оценочным тестом. Мы покажем позднее, что эта аппроксимация не ухудшает полезность метода.

МКП может быть расширен синхронными последовательностными схемами, которые используют модель итерационного массива. В этой статье мы ограничиваемся комбинационными схемами.

2. Основные идеи

Определение 1: Линия l имеет критический путь на тесте (векторе) t, если t обнаруживает неисправность l s-a-v#. Будем говорить, что линия с критическим путём в t является критической в t.

В отличии от понятия D-символа (нотация) в D-алгоритме [Roth67], критический путь всегда указывает на обнаружение неисправности.

Очевидно, что PОs являются критическими в любом тесте. Исследуемый метод состоит в определении путей с критическими линиями, называемыми критическими путями. Это происходит при трассировке процесса в обратном направлении, который стартовал с PОs. Найдя критическую линию в тесте t, мы немедленно определяем неисправности обнаруженные t.

Определение 2: Вход вентиля i является чувствительным, если изменение его значения на противоположное (инверсия) приводит к изменению значения выхода вентиля.

МКП стартует после моделирования схемы в исправном состоянии (исправного моделирования) для теста t. С целью последующей обратной трассировки, мы маркируем чувствительные входы во время выполнения моделирования исправной схемы. Чувствительные входы однородных контактов с двумя или более входами легко определяются следующим образом:
1) если только один вход i имеет Доминантное входное значение (ДВЗ), тогда i – чувствительный (для И и НЕ-И ДВЗ=0; для ИЛИ и ИЛИ-НЕ ДВЗ=1);
2) если все входы имеют значения ДВЗ# (неДВЗ), тогда все входы являются чувствительными;
3) иначе, ни один вход не является чувствительным.

Маркирование чувствительных входов во время моделирования исправной схемы приводит к возникновению небольшого переполнения, начиная с момента поиска входов по ДВЗ, который относится к совместно используемым методам логического анализа.

Для начала мы покажем МКП для схемы без разветвления (см. рис. 1). На рисунке 1а изображёны результаты моделирования схемы в исправном состоянии с чувствительными входами, которые помечены точками. На рисунке 1б критические пути отмечены толстыми линиями. Для схемы без разветвления, которая всегда имеет древовидную структуру, МКП является обычной процедурой обхода вершин дерева, отмечающей критические вершины. МКП рекурсивно следит за каждым изменением чувствительного входа вентиля с критическим выходом. Это следует из того, что, если выход вентиля является критическим, то чувствительные входы вентиля, если таковые имеются, будут также критическими. Например, на рис. 1 показано, как МКП полностью игнорирует ту часть схемы, которая граничит с линиями В и С, так как, работая в обратном направлении от РО, МКП сначала определяет, что линии В и С не являются критическими.

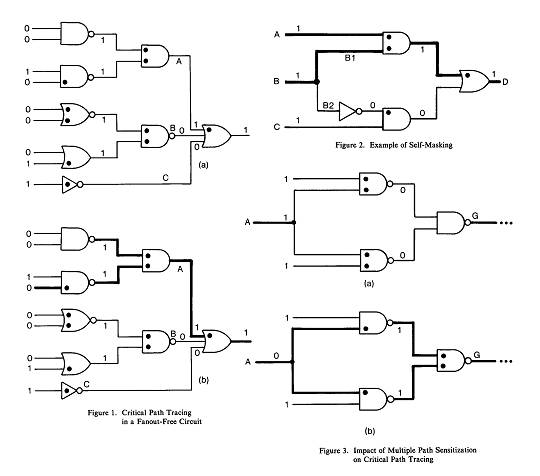
Теперь обсудим общий случай, когда схема имеет сходящееся разветвление. При использовании прикреплённой модели неисправности для сигнала с разветвлением, будем различать его ствол и разветвлённые ветви (FOBs). Например, на рис. 2 линии В1 и В2 – FOBs ствола В. Сложность в распространении критического пути в схеме с разветвлёнными входами при использовании МКП появляется, когда ствол является критическим, то есть хотя бы одна из его FOBs – критическая. На рис.2 мы можем не распространять критический путь от В1 до В потому, что эффект неисправности В s-a-0 распространяется по двум путям с разным числом инверсий по чётности. Это правило действует с учётом того, что эти пути исключают друг друга, когда сойдутся на вентиле D. Этот случай называется самомаскированием.

Далее рассмотрим подход Хонга. Разделим задачу оценки теста на две подзадачи: первая будет оперировать с фрагментами без разветвлений (FFRs), вторая – с таковыми (со стволами). Алгоритм, взятый из, предполагает сначала определить обнаруживаемость неисправностей в стволах явным моделированием неисправности, а затем построить критические пути в каждом FFR, для которого была обнаружена неисправность в его стволе. Комбинированный алгоритм представляет собой улучшение явного моделирования всех неисправностей. Наш алгоритм направлен на определение обнаруживаемых неисправностей в стволе, которые возникают во время обратной трассировки при использовании нового типа анализа, его мы покажем позднее, который более эффективен, чем явное моделирование неисправности. Этот анализ описан в следующем пункте.

Другая особенность сходящегося разветвления состоит в том, что неисправности, которые обнаруживаются только многомерной активизацией путей могут быть объявлены необнаруживаемыми, как показано на рис. 3а. Здесь нет критических входов вентиля G, но неисправность на А обнаружена при двумерной активизации пути. МКП работает с неразрывными цепочками критических линий, он не распознает ствол А как критический в этом тесте; следовательно, это только приближённый метод. Мы рассмотрим применение этого приближения в пункте 4.

Отметим, что случай, когда активизируется многомерный путь от ствола, который имеет #ДВЗ на сходящихся вентилях (рис. 3б) не представляет собой никаких проблем для нашего метода.

3. Алгоритм МКП

Сначала мы выполним предварительную обработку схемы с целью определения её конусов (?), где под конусом подразумевается подсхема с одним РО (Primary Output). Мы представляем конус как взаимосвязь FFRs (Fanout-Free Regions). На рис. 4б показаны эти структуры как дополнение к рис. 4а. Входы FFR являются FOBs (FanOut Branches) и/или PIs. Выход FFR является также РО или стволом. Отметим, если линия i является стволом, то она может зависеть от конуса, который её содержит. Например, N и CI – будут стволами в конусе S, но не будут таковыми в конусе СО. Построение конусов и FFRов обычно выполняется как шаг предварительной обработки при генерации теста для LSSD схем.

На рис. 5 изображён алгоритм для оценки одного теста. Предполагается, что исправное моделирование, которое включает в себя маркирование чувствительных входов вентилей, уже было выполнено. Алгоритм обрабатывает каждый конус, начиная с его РО и чередуясь между двумя его операторами: МКП внутри FFR, представленный процедурой Extend, и проверка ствола на критичность, выполненная в процедуре Critical. Как только обнаруживается, что ствол j является критическим, МКП продолжается с j.

На рис. 6 изображена рекурсивная процедура Extend(i), которая выполняет обратную трассировку всех критических путей внутри FFR, начиная с данной критической линии i и следуя по линиям, отмеченными чувствительными. Extend останавливается на входах FFR и собирает все стволы, удовлетворяющие Stems_to_check.

Каждый ствол в Stems_to_check имеет по крайней мере одну критическую FOB. Алгоритм всегда выбирает для анализа ствол с самым высоким уровнем (т.е. самый близкий к РО), и, следовательно, гарантирует, что статус (критический/не критический) всех его FOBs известен. Ключевым элементом алгоритма является процедура Critical(j), которая определяет, является ли ствол j критическим.

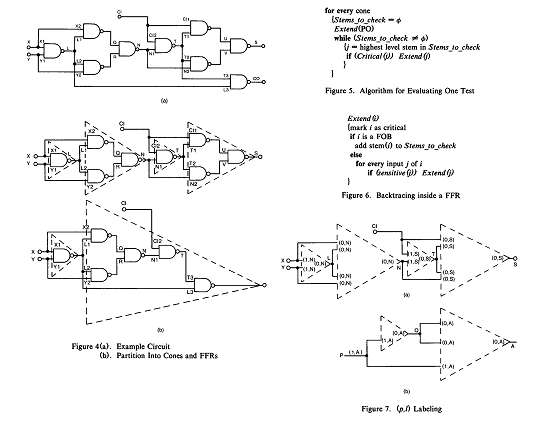
Для определения критичности ствола мы выясним, встречается ли на этом участке самомаскирование.

Частный случай.
Для начала мы покажем методику частного случая предварительной обработки, которая позволяет нам непосредственно идентифицировать некоторые стволы, как критические, без какого-либо анализа. Когда конус построен по топологической обратной трассировке, начинающейся с его PО, с каждым входом FFR и выходом i, мы ставим ему в соответствие метку (p, l), определённую следующим образом.

Определение 3: Линия i имеет (p, l)-метку, если все пути конуса от i до РО проходят через l, и каждый путь от i до l имеет паритет p.

На рис. 7а показаны (p, l)-метки конуса S. Ясно, что все входы FFR имеют одинаковое l. Если все FOBs ствола j имеют одинаковую (p, l)-метку, тогда считается, что они относятся к стволу; иначе j присваивается метка (0, j). Следующее правило позволяет нам отмечать стволы, как критические, без дополнительного анализа.

Правило 1: Если ствол j имеет метку (p, l), при l j, тогда всякий раз, когда j будет достигаться обратной трассировкой, он всегда может быть обозначен как критический.

Доказательство: Линия j может быть достигнута во время обратной трассировки только в том случае, если уже доказано, что l – критическая. Так как все пути от j до l имеют одинаковый паритет, то между j и l не может произойти самомаскирование. Следовательно, неисправность на j будет распространяться к l, и, так как l – критическая, неисправность также распространится к РО. Поэтому j также является критической.

На рис. 7а показаны (p, l)-метки конуса S из рис. 4. В соответствии с Правилом 1, Critical немедленно вернёт TRUE для стволов L и T. Заметим, что метка, сделанные в конусе, как L, должна быть проверены на критичность в конусе СО. В нашем примере, и L, и T имеют свои FOBs, питающие один и тот же FFR. Рис. 7б показывает различные ситуации, в которых ствол (Р) не требует проверки.

Общий случай.
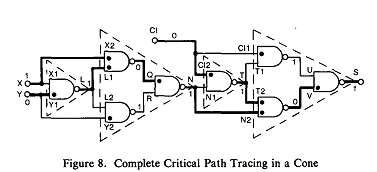
Для иллюстрации принципа, использованного в Critical(j), для проверки ствола j, который не удовлетворяет Правилу 1, рассмотрим конус S для теста (X, Y, CI)=100 (см. рис. 8). После выполнения Extend(S), что T2 и N2 – критические. В этот момент Stems_to_check = {T, N}. Critical(T) немедленно возвращает TRUE и Extend(Т) помечает линию CI2 как критическую. Теперь Stems_to_check = {N, CI} и линия N выбрана для анализа. Для пояснения, предположим, что мы симулируем неисправность s a-0 (константа ноль) на N. Эффект этой неисправности начнёт распространяться по двум путям, один из которых начинается от критической FOB (N2), а второй – от некритической FOB (N1). Самомаскирование может произойти только, если распространение по последней дорожке, названное потенциальным маскированием, «убивает» распространение неисправности по критическому пути, как показано на рис. 2. Легко определить, что этот тип схождения не происходит на рис. 8, так как потенциальное маскирование пути будет немедленно прекращено на вентиле Т, поскольку этот путь входит в вентиль через вход, не отмеченный как чувствительный. Следовательно, мы можем сразу сделать вывод, что N – критическая. Мы подчёркиваем, что в распространении вдоль критического пути вне N2 нет необходимости, потому что мы уже определили, что все эффекты потенциального маскирования неисправности исчезли. Это похоже на идею, использованную в одиночном распространении неисправности.

Алгоритм.
На рис. 9 показана процедура Critical(j). Сначала анализируется (p, l)-метка ствола j для определения, применимо ли Правило 1 для этого ствола. Если нет, то проверка критичности j неявно содержит след распространения эффектов неисправности j вдоль критических путей против (в направлении, обратном) распространения при потенциальном маскировании путей. Две границы(?) распространения реализованы в списках Prop_crit и Prop_noncrit. Эти списки состоят только из FOBs и стволов. FFRlist – это список из FFRs, непосредственно питаемых элементами списков Prop_crit и Prop_noncrit. По алгоритму всегда выбирается для проверки FFR с самым низким уровнем FFR из FFRlist, и, следовательно, это гарантирует, что статус всех входов FFR, относительно распространения неисправности на j, известен. Процедура FFRcheck (i) определяет распространение двух границ через FFR i; следовательно, это неявно определяет, достигают ли эффекты неисправности со входов FFR на их выходы. Существенной особенностью FFRcheck (i) является то, что процедура обычно «прыгает» от входов FFR i к их выходам без трассировки вентилей, находящихся внутри FFR. Следующий пример показывает различные случаи FFR-прыжков. (Подробное описание алгоритма выходит за рамки этой статьи.)

Пример.
Предположим, что линии, в настоящее время определённые как критические, показаны на рис. 10, и сейчас стоит задача определить, является ли А критической. Таблица отображает выполнение Critical(A).

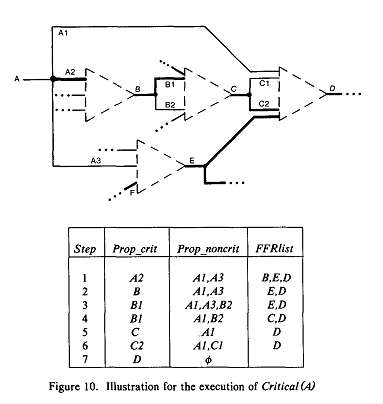
Шаг 1: Начинаем с Prop_crit={A2} и Prop_noncrit={A1, A3}, первой проверяемой FFR будет В, которая достигается только линиями в Prop_crit={A2}. Здесь маскирование не может проникнуть внутрь FFR, следовательно, эффект неисправности на А2 распространяется на В; поэтому мы добавляем В в Prop_crit.

Шаг 2: FOBs ствола В (В1 и В2) добавлены к двум границам, основанных при первичном определении критичностей.

Шаг 3: Далее мы анализируем FFR Е, которая достигается только одной линией в Prop_noncrit(A3). Так как Е имеет критический вход (F), то распространение от А3 до Е обязано будет остановиться внутри FFR. Причиной, по которой должен существовать вентиль G, где путь от А3 будет сходиться с критическим путём F, будет то, что критический вход G имеет ДВЗ.

Шаг 4: FFR С достигается линиями с обеих границ – В1 в Prop_crit и В2 в Prop_noncrit. Но распространение от В2 не может остановить распространение от В1, потому что алгоритм уже определил ствол В как критический. Поэтому мы добавляем С в Prop_crit.

Шаг 5: FOBs ствола С добавляются к двум границам.

Шаг 6: Критерий, который мы использовали для пропуска FFR С, не может быть использован для FFR D из-за дополнительной потенциально маскируемой линии, которая достигает (А1); А1 не играет никакой роли при определении критичности С. Теперь мы применим другой критерий для избежания трассировки в FFR. Пусть p(A1), p(C1), p(C2) обозначают, соответственно, инверсные паритеты между А1, С1 и С2, и D. Пусть v(A1), v(C1) и v(C2) будут их текущие значения. Это показывает, что, если v(A1) XOR p(A1)=v(C1) XOR p(C1)=v(C2) XOR p(C2), то маскирование не может проникнуть внутрь FFR D. Предполагая, что это равенство удовлетворено на рис. 10а, мы добавляем D в Prop_crit.

Шаг 7: К этому моменту Prop_noncrit= и |Prop_crit|=1 (так как Prop_crit={D}); следовательно, процедура возвращает определение линии А как критической.

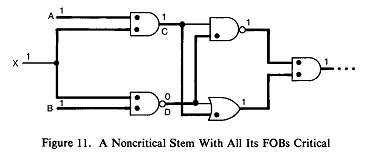
Можно задаться вопросом, почему одного условия Prop_noncrit=0 не достаточно для прекращения дальнейшей трассировки. Ответ показан в примере на рис. 11, который изображает ствол (Х), все FOBs которого – критические (следовательно Prop_noncrit=0). Однако, вопреки интуиции, Х – не критический. Причина в том, что потенциально маскируемой линии появляется после распространения через С и D. Требование Prop_noncrit=0 и |Prop_crit|=1 гарантирует то, что маскирование далее произойти не может.

Если ни один из критериев «FFR прыжка» не применяется, то трассировка пути происходит внутри FFR. Это подобно трассировке пути на FFR-уровне, то есть, распространение границ Prop_crit и Prop_noncrit происходит в первую очередь. Отметим, что никакие оценки вентилей не происходят, и даже типы вентилей и значения сигналов не нужны для этого анализа; единственно необходимая информация определяется при чувствительном маркировании.

Мы подчёркиваем, что в большинстве случаев самомаркирование не происходит и распространение потенциально маркируемых эффектов неисправности скоротечно, поэтому обычно необходимо небольшое усилие для определения, является ли ствол критическим.

Наш метод состоит из следующих шагов:
1) Предварительная обработка схемной модели, с целью определения её конусов, FFR-структур и (p,l)-меток.
2) Исправное моделирование одного теста и идентификация чувствительных входов вентилей.
3) МКП является процессом обратной трассировки, который идентифицирует критические линии (и отныне обнаруженные неисправности) теста, моделируя шаг 2.
Шаги 2 и 3 повторяются для каждого теста в наборе тестов, который оценивается.

4. Выводы

Ключевые факторы, содействующие увеличеннию эффективности МКП по сравнению с моделированием неисправности, следующие:
• МКП оперирует только обнаруженными неисправностями, вместо всех возможных неисправностей;
• МКП оперирует неисправностями только косвенно, вместо того, чтобы это делать явно;
• МКП является приближённым методом, вместо точных.

Введение приближения негативно и заключается в немаркировании, как обнаруживаемых, некоторых неисправностей, обнаруженных при многомерной активизации пути с ДВЗ сходящихся вентилей. Это явление происходит редко. Однако, мы показали, что приближение не воздействует на процесс генерации теста и не имеет практически никакого влияния на другие приложения МКП.

Преимущества оценки теста МКП, перед обычными методами явно свидетельствуют, что решения проблем VLSI-тестирования должны быть основаны на приближённых алгоритмах, которые быстрее и, в общем, точнее. Выгода одного направления в течение времени выполнения гораздо более важна, чем "точный" алгоритм, единственным преимуществом которого является правильная обработка ситуаций, которые происходят редко. К тому же, МКП может учитывать преимущества точных и дорогих алгоритмов для приближённой модели неисправности.

Ссылки

[ArWa81] Y. Arzoumanian and J. Waicukauski, "Fault Diagnosis in an LSSD Environment," Proc. 1981 International Test Conference, pp. 86-88, October, 1981.

[BrFr76] M. A. Breuer and A.D. Friedman, "Diagnosis and Reliable Design of Digital Systems," Computer Science Press, 1976.

[Cha 78] C. W. Cha, W.E. Donath and F. Ozguner, "9-V Algorithm for Test Pattern Generation of Combinational Digital Circuits," IEEE Trans. Comput., Vol. C-27, No. 3, pp. 193-200, March, 1978.

[EiWi771 E. B. Eichelberger and T. W. Williams, "A Logic Design Structure for LSI Testability," Proc. 14th Design Automation Conference, pp. 462-468, June, 1977.

[Goel80a] P. Goel, "Test Generation Costs Analysis and Projections," Proc. 17th Design Automation Conference, pp. 77-84, June, 1980.

[Goel80b] P. Goel, et al, "LSSD Fault Simulation Using Combinational and Sequential Methods," Proc. Conference, pp. 371-376, November, 1980.

[Hong78] S. J. Hong, "Fault Simulation Strategy for Combinati Logic Networks," Proc. 8th International Syrup. Fault-Tolerant Computing, pp. 96-99, June, 1978.