Автореферат

квалификационной работы магистра

"Прогнозирование погодных условий по временным рядам метеовеличин"

Введение, обоснование актуальности

Известное выражение «О погоде поговорить каждый любит...» отражает собой тот огромный интерес, который проявляет человек к окружающей его атмосферной среде. Этот интерес затрагивает и отдельных людей, и их сообщества, и нации, и человеческое общество в целом. Ежесуточная сводка погоды, например, заставляет человека принимать различные решения: брать ли ему зонтик или заниматься поиском убежища от надвигающегося урагана.

В развитых странах погода и климат давно стали категориями экономическими. Каждый год в мире стихийные бедствия уносят около 250 000 человеческих жизней, размер ущерба, наносимого имуществу, лежит в пределах 50-100 млрд. долларов США. Но мировая статистика показывает: если доверять гидрометеорологической информации и адекватно на нее реагировать, то можно предотвратить от 30 до 40% потерь и полностью избежать человеческих жертв [1].

Особенно заметный экономический эффект дает использование метеорологической информации в авиации, энергетике, строительстве, рыболовстве и судоходстве, сельском хозяйстве.

Предсказание погоды с научной точки зрения – одна из сложнейших задач физики атмосферы. Существуют различные методы для прогнозирования метеорологических явлений и их величин, например, синоптические, численные, статистические методы, но в полном объеме ни один метод не обеспечивает пока точного прогноза. Именно поэтому исследования в области прогнозирования погодных условий являются важными и полезными, а тема – актуальной.

Цели и задачи

Цель дипломной работы – изучение возможности прогнозирования метеопараметров по их временным рядам и, в идеале, формирование и отработка на их основе методики расчета краткосрочного прогноза погоды. Такие временные ряды предоставляются, в частности, автоматизированными метеостанциями типа Vantage Pro 2 [2]. Одна из таких установлена на факультете вычислительной техники и информатики ДонНТУ.

Идея работы заключается в анализе и использовании временных рядов метеовеличин для создания модели прогноза погоды адаптированной под Донецкий регион.

Задачи, решаемые в магистерской работе:

• изучение литературных источников по методам прогнозирования по временным рядам;
• сбор и анализ метеоданных для установления статистических закономерностей;
• разработка математической прогностической модели;
• разработка системы прогнозирования, оценка ее адекватности.

Объектом исследования является система метеорологических показателей города.

Предметом исследования являются модели прогнозирования погоды.

Методы исследований – визуальный, статистический и спектральный анализ данных, метод ложных соседей определения аргументов модельных функций, методы аппроксимации функций многих переменных с помощью обобщенных многочленов, радиальных базисных функций, искусственных нейронных сетей и т.д.

Предполагаемая научная новизна

Научная новизна исследований заключается в:

• формировании методики расчета краткосрочного прогноза погоды по временным рядам метеовеличин;
• разработке программного обеспечения, реализующего эту методику.

Обзор исследований и разработок по теме

Еще на заре своей истории человек сталкивался с неблагоприятными атмосферными явлениями. Не понимая их, он обожествлял грозные и стихийные явления, связанные с атмосферой (боги – Перун, Зевс, Дажбог и др.). По мере развития цивилизации в Китае, Индии, странах Средиземноморья делаются попытки регулярных метеорологических наблюдений, появляются первые научные представления о климате. Первый труд об атмосферных явлениях был составлен Аристотелем. Современная научная метеорология ведет начало с XVII в., когда были заложены основы физики. Великим ученым Галилеем и его учениками были изобретены термометр (1610г.), барометр, дождемер, то есть появилась новая возможность инструментальных наблюдений. Начиная с середины XVII века академия экспериментирования в Тоскане организовало первую немногочисленную сеть инструментальных наблюдений, которые проводились в нескольких пунктах Европы. Кроме того, непременной частью программ всех морских плаваний было проведение наблюдений за погодой.

В это же время появились первые метеорологические теории. Э. Галлей дал первое объяснение муссонов, а Э. Гадлей опубликовал трактат о пассатах. К середине XVIII в. М. В. Ломоносов считал метеорологию самостоятельной наукой, главной задачей которой было "предзнание погоды". Было организовано по частной инициативе Маннгеймское метеорологическое общество, которое создало в Европе на добровольной основе сеть из 39 метеорологических станций (в том числе три в России – Санкт-Петербурге, Москве, Пышменский завод), укомплектованных единообразными и проградуированными приборами. Сеть функционировала 12 лет.

В середине XIX в. возникают государственные сети станций. А в начале века трудами А. Гумбольдта и Г. Дове в Германии закладываются основы климатологии. Около 1820 года Г. В. Брандесу в Германии пришла мысль нанести на географические карты наблюдения Маннгеймской сети станций. Таким образом, появились первые синоптические карты, позволившие обнаружить области высокого и низкого давления. Они оказались подвижные и двигались, как правило, с запада на восток. После изобретения телеграфа, с 50-х годов, по инициативе астронома У. Леверье во Франции и адмирала Р. Фицроя в Англии синоптический метод исследования атмосферных фронтов быстро вошел в общее употребление. На его основе возникла новая отрасль метеорологии – синоптическая метеорология.

К середине XIX в. относится организация первых метеорологических институтов, в том числе Главной физической обсерватории в Петербурге (1849г.). Во второй половине XIX столетия были заложены основы динамической метеорологии, т. е. применения законов гидромеханики и термодинамики к исследованиям атмосферных процессов. Большой вклад в эту область метеорологии был сделан Кориолисом и Пуассоном во Франции, В. Феррелем в США, Г. Гельмгольцем в Германии, Г. Моном и К. Гульдбергом в Норвегии. К концу столетия усилилось изучение радиационных и электрических процессов в атмосфере [3].

Развитие метеорологии в XX веке шло нарастающими темпами. Впервые задачу прогноза погоды как задачу гидротермодинамики с начальными и краевыми условиями сформулировал Бьеркнес в 1904 году в докладе на конференции в Берлине.

Попытку решить такую систему уравнений с помощью разностных методов осуществил во время Первой Мировой войны Ричардсон. Он с группой сотрудников английской метеослужбы попытался дать прогноз для района Нюренберг-Аугсбург на одни сутки. Однако эта попытка оказалась неудачной – ошибка в приземном поле давления через 6 часов составила величину порядка сотен миллибар. Ричардсон использовал неустойчивую разностную схему (в то время теории устойчивости разностных схем не существовало), и в своих расчетах использовал уравнения, которые требовали начальных данных для поля ветра. Эти поля он получал из данных наблюдений, получая при этом гигантскую ошибку в поле дивергенции, ответственной за преобразование энергии.

Следует упомянуть фундаментальные работы Карла Густава Россби и Ильи Афанасьевича Кибеля, оказавших решающее влияние на развитие численных методов прогноза погоды. В их работах в уравнениях прогноза погоды был выделен малый параметр, с помощью которого можно было проводить обоснованные упрощения исходных уравнений. В конце двадцатых годов вышла также работа Куранта, Фридрихса и Леви, установившая ограничения на выбор пространственных и временных шагов при численном решении уравнений математической физики [4].B 1946 году Джон фон Нойман собрал небольшую группу молодых ученых (ведущим в этой группе был Дж.Чарни) перед которой была поставлена задача численного прогноза погоды. Первый успешный численный прогноз был сделан этой группой в 1950 году.

Следующий принципиальный шаг, связанный с формулированием квазигеострофического приближения, был сделан почти одновременно Дж.Чарни и А.М. Обуховым.

В эти же годы появились первые (ставшие классическими) работы, посвященные исследованию устойчивости по Ляпунову зонально-симметричных атмосферных потоков. Эти работы показали, что при разумных значениях параметров Атмосферные потоки являются неустойчивыми по отношению к малым возмущениям начальных данных. Итак, после формулирования квазигеострофического приближения встала задача реализации его в виде численной схемы прогноза погоды. Такие реализации были построены в 1952 году Н.И.Булеевым и Г.И.Марчуком. Метод был основан на построении функции Грина для тенденции геопотенциала и был реализован С.Л.Белоусовым в виде оперативной схемы прогноза погоды в Гидрометцентре СССР.

Уже в эти годы ученые пришли к выводу, что неустойчивость атмосферных потоков по отношению к ошибкам начальных данных приводит к ограничению времени полезного прогноза. Аналогичные ограничения следовало ожидать и от ошибок, содержащихся в упрощенных уравнениях, поэтому в начале 60-х годов была сформулирована проблема создания численной схемы прогноза погоды на основе полных уравнений гидротермодинамики атмосферы с учетом всех значимых неадиабатических факторов.

На первых этапах решения этой проблемы центральной задачей была разработка эффективных численных методов решения гиперболических нелинейных уравнений. В 1966 году вышла работа А.Аракавы, в которой он предложил метод построения разностной схемы для уравнений двумерной несжимаемой жидкости, обладающей двумя квадратичными инвариантами. В этом же году Кирк Брайен предложил метод конечных объемов (в современной терминологии).

В середине 60-х годов Г.И.Марчук предложил для решения уравнений гидротермодинамики атмосферы абсолютно устойчивые неявные схемы, основанные на методе расщепления по физическим процессам и геометрическим переменным [5]. Этот метод был положен в основу разработанной в ВЦ СО АН СССР численной схемы прогноза погоды по полным уравнениям, внедренной затем в оперативную практику Западно-Сибирского УГМС.

Долгое время спектральный метод был достоянием только метеорологической научной среды и использовался для решения уравнений динамики атмосферы. В 60-х годах спектральный метод, или метод Галеркина, в котором в качестве базисных функций используются сферические гармоники, был не конкурентоспособным ,по сравнению с разностными методами, из-за большого количества арифметических операций и использовался только в моделях малой размерности. Однако, после открытия Орзагом спектрально-сеточного преобразования, он занял ведущее место при конструировании моделей прогноза погоды и общей циркуляции атмосферы.

В конце 60-х - начале 70-х годов в результате большой серии численных экспериментов было выработано представление, что предел "детерминированной" предсказуемости составляет величину порядка двух недель (некоторые оценки давали три недели) и на повестку дня вышла задача создания модели среднесрочного прогноза погоды (1-7 дней). Базой создания таких моделей должны были стать быстро развивающаяся вычислительная техника, развитие наблюдательной сети – большие надежды возлагались на спутниковые наблюдения и научные разработки параметризаций процессов подсеточных масштабов, объективного анализа данных наблюдений и др. Эта программа была осуществлена в созданном в 1975 году Европейском центре среднесрочных прогнозов погоды. Основным результатом этой работы,выполненной под руководством Л.Бенгтсона, была разработка высокой технологии - системы четырехмерного усвоения данных, позволившей вывести прогностическую систему Европейского Центра на первое место в мире. Решение этой проблемы было возможно только на основе результатов Первого глобального эксперимента, которые позволили определять качество модели - ее способность эффективно усваивать асинхронные данные.

Первую численную модель общей циркуляции атмосферы на основе квазигеострофических уравнений (двуслойная модель) построил Н. Филлипс. В начале 60-х годов Д. Смагоринский, возглавив вновь образованную в Принстоне Лабораторию геофизической гидродинамики, сформулировал программу последовательного изучения роли различных неадиабатических факторов в формировании обшей циркуляции атмосферы с помощью численных моделей, основанных на полных уравнениях гидротермодинамики.

Одновременно началась разработка моделей общей циркуляции океана, и на основе этих моделей совместной модели общей циркуляции атмосферы и океана, которая должна была стать основой глобальной климатической модели. В Советском Союзе такая программа была сформулирована в начале 70-х годов в Вычислительном центре СО АН СССР (Г.И.Марчук) и успешно реализовывалась в течение последующих 20 лет сначала в ВЦ, а затем в Институте вычислительной математики РАН. Параллельно большое внимание также уделялось проблеме прогноза изменений климата под влиянием антропогенной деятельности человека, в частности, под влиянием увеличения концентрации углекислого газа в атмосфере.

Большой вклад внесла группа сотрудников уже упомянутой Лаборатории геофизической гидродинамики, руководимая Суки Манабе. Ими была высветлена фундаментальная проблема в теории климата – проблема чувствительности климата к малым внешним воздействиям и формализована на основе теории диссипативных динамических систем. В 90-е годы в Институте вычислительной математики РАН под руководством В.П.Дымникова было выполнено формулирование методов построения операторов отклика климатической системы на малые внешние воздействия. Ключевым моментом этого подхода было исследование структуры аттракторов климатических моделей и их устойчивости.

Следует подчеркнуть, что развитие моделей прогноза погоды и климата напрямую стимулировалось развитием вычислительной техники. Три революции в вычислительной технике, происшедшие в последние 30 лет - переход на интегральные схемы, создание машин с конвейерными вычислениями и создание параллельных вычислительных систем с быстрой коммуникацией привели к разработке высоких вычислительных и информационных технологий в проблеме прогноза погоды. В основе этих технологий лежат методы решения трех задач - непосредственно задачи прогноза погоды, задачи инициализации начальных данных (ликвидация шока гравитационных волн в начальный момент времени) и задачи четырехмерного усвоения данных. Решение проблемы предсказуемости ищется с помощью использования в начальный момент времени некоторого распределения ошибок начальных данных, т.е. решения не одной, а серии прогностических задач. Этот метод идеально ложится на структуру параллельных вычиелнтельных систем [6].

Апробация

Результаты роботы докладывались на V международной конференции студентов, аспирантов и молодых ученых «Компьютерный мониторинг и информационные технологии» (КМИТ-2009) и опубликованы в соответствующем сборнике.

Текущие и планируемые результаты

Несмотря на безграничное число ситуаций, объектов и целей, вносящих в процесс свое специфическое, можно выделить основные этапы моделирования и представить их в виде схемы (рис. 1). Работа начинается с рассмотрения имеющейся информации об объекте (экспериментальных данных о нем самом или подобных объектах; теорий, разработанных для описания исследуемого класса объектов; интуитивных представлений и т.д.) с позиций цели исследования, с получения и предварительного анализа рядов наблюдаемых величин, а заканчивается использованием полученной модели для решения конкретной задачи. Но этот процесс обычно является итерационным – сопровождается неоднократными повторениями, возвратами в исходную и промежуточные точки схемы, последовательными приближениями к «хорошей» модели.

Рисунок 1 – Типовая схема процесса эмпирического моделирования

Рассмотрим более подробно каждый этап.

На первом этапе осуществляется получение данных и их систематизация. Далее применяется один или несколько методов анализа имеющихся временных рядов наблюдаемых метеовеличин. Это, например, визуальный анализ в виде графиков зависимости переменной от времени, восстановление фазовой траектории, спектральный и статистический анализ и другие [7].

На ключевом в схеме этапе 2 формируется структура модели. Первоначально выбирается тип уравнений, далее задается вид входящих в них функций, после чего устанавливается связь динамических переменных (компонент вектора x) с наблюдаемыми величинами a. В качестве переменных могут выступать сами наблюдаемые, но в более общем случае эту связь задают в виде a = h(x) , где h называют измерительной функцией. Часто вводят еще случайную добавку e: a = h(x) + e, чтобы учесть измерительный шум. Чтобы сделать модель более реалистичной, случайную добавку вводят нередко и в сами уравнения – так называемый динамический шум.

Формирование структуры модели – наиболее сложный и творческий этап процедуры моделирования. На данном этапе выбирается тип уравнений, вид входящих в них функций и их аргументов.

Задача определения аргументов функции состоит в том, чтобы определить наименьшую размерность модели, обеспечивающую однозначность прогноза. Для решения этой задачи используется различные методы оценки: метод ложных соседей, метод главных компонент, метод Грассбергера – Прокаччиа, метод хорошо приспособленного базиса. Первый из них заключается в следующем.

Он основан на проверке того свойства, что фазовая траектория, восстановленная в пространстве достаточной размерности не должна иметь самопересечений. При пробной размерности D для каждого восстановленного вектора x_k отыскивают одного (самого близкого) соседа; увеличив D на 1, определяют, какие из соседей оказались ложными (сильно разошлись), а какие – истинными. Подсчитывают отношение числа ложных соседей к общему числу восстановленных векторов. Если при увеличении D это число становится малым при некотором значении D*, то последнее и есть оценка размерности пространства, в котором достигается вложение траектории моделируемого движения [7].

Далее следует этап определения структуры модельных уравнений. Для этого используются различные методы аппроксимации функций многих переменных: метод обобщенного многочлена, использование радиальных базисных функций, искусственные нейронные сети, локальные модели, поиск близких соседей.

Рассмотрим некоторые из них.

1) Метод обобщенного многочлена.

Для построения глобальной модели выбирают вид f и рассчитывают параметры обычным МНК, т.е. требуют, чтобы

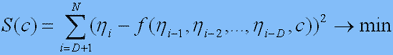(1)

Для простоты расчетов желательно выбрать функцию f, линейную относительно c. Это имеет место для так называемого обобщенного многочлена по некоторой системе базисных функций f₁,f₂,...,f_p:

(2)

При этом задача (1) линейна и не возникает проблемы локальных минимумов. К такому способу относится использование алгебраического многочлена, порядок которого увеличивается, пока не будет найдена адекватная модель.

2) Радиальные базисные функции.

Это функции вида ф_k(x)=ф(||x-a_k||/r_k), где ||·|| означает норму (длину) вектора. В качестве «материнской» функции ф обычно берется хорошо локализованная функция, например, «гауссиана» ф(y)=exp(-y²/2), величины a_k называют «центрами», а r_k – «радиусами». Модельная функция f представляет собой обобщенный многочлен по системе функций:

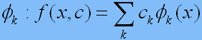
Каждое слагаемое существенно отлично от нуля только на расстоянии, не большем r_k от центра a_k. Интуитивно ясно, что с помощью такой суперпозиции можно приблизить достаточно сложный рельеф.

3) Искусственные нейронные сети (ИНС).

Модели с ИНС широко и успешно используются для решения многих задач. Они представляют собой не сумму базисных функций, а их композицию. В отличие от обобщенного многочлена, они обязательно нелинейно зависят от оцениваемых параметров.

Опишем ИНС формально на примере многослойного персептрона. Пусть x=(x₁,...,x_p) – аргумент искомой функции f. Составим набор функций: f_j⁽¹⁾(x), j=1,...,K₁:

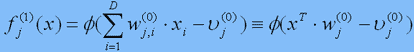(3)

где постоянные w_j,i⁽⁰⁾ называют весами, u_j⁽⁰⁾ – порогами, ф – функцией активации. Функция ф обычно нелинейна и имеет график ступенчатого вида. Каждая функция f_j⁽¹⁾ представляет выход стандартного формального нейрона с номером j, на вход которого подан вектор x. Система функций f₁⁽¹⁾,...,f_k1⁽¹⁾ – это набор нейронов первого слоя. Назовем значения функций f_j⁽¹⁾ выходными значениями нейронов первого слоя и обозначим их совокупность вектором y⁽¹⁾ с компонентами y_j⁽¹⁾=f_j⁽¹⁾(x).

Определив в качестве функции f линейную комбинацию f₁⁽¹⁾, получим так называемую однослойную ИНС:

,

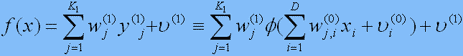где параметры w_j⁽¹⁾,u⁽¹⁾ – дополнительные веса и порог.

Свободных параметров в такой модели P=K₁(D+1)+(K₁+1) штук. Это представление похоже на обобщенный многочлен (2), но ИНС нелинейно зависит от параметров w_j,i⁽⁰⁾ и u_i⁽⁰⁾.

Рассмотрим теперь еще одну систему функций f_j⁽²⁾, j=1,...,K₂, имеющих вид (3), но зависящих от K₁-мерного аргумента. Это нейроны второго слоя, на вход которых подаются выходы нейронов первого слоя y⁽¹⁾. Обозначим их выходные значения вектором y⁽²⁾ размерности K₂ и определим функцию f как линейную комбинацию выходных значений нейронов второго слоя:

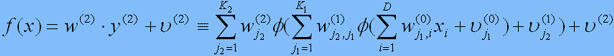
Это двухслойная ИНС, которая включает в себя уже композиции функций, что существенно отличает ее от псевдолинейной модели (2). Увеличение числа слоев достигается очевидным образом.

Чаще всего для решения задач аппроксимации используют двухслойные ИНС, реже – трехслойные [8]. Увеличение числа слоев не приводит к существенному улучшению. Улучшения добиваются за счет увеличения числа нейронов в слоях K₁,K₂. Теоретическая основа использования ИНС – обобщенная аппроксимационная теорема (ее частным случаем является теорема Вейерштрасса), которая утверждает, что любая непрерывная функция может быть сколь угодно точно равномерно приближена с помощью ИНС [9].

Процедура расчета параметров ИНС путем минимизации – ее «обучение» – это сложная задача многомерной нелинейной оптимизации, для решения которой развиты специальные «технологии»: алгоритм обратного распространения ошибки, обучение с расписанием, обучение с шумом, стохастическая оптимизация (генетические методы, метод имитации отжига) [10]. ИНС может содержать очень много лишних элементов, и структуру этой модели (архитектуру сети) желательно сделать более компактной. Для этого нейроны, веса и пороги которых слабо меняются в процессе обучения, исключаются из сети.

Если имеется несколько альтернативных ИНС с разной архитектурой, полученных в результате обучения по тренировочному ряду, то лучшую из них обычно выбирают по наименьшей тестовой ошибке аппроксимации. Для получения «честного» показателя прогностической эффективности модели используют еще один ряд (не тренировочный и не тестовый, т.к. оба они использовались для построения модели), который называют «экзаменационным».

После выбора структуры выполняют «подгонку модели». Для этого, как правило, проводится поиск экстремального значения некоторой целевой функции, например, минимизируется сумма квадратов отклонений решения модельных уравнений от наблюдаемых данных. При необходимости на данном этапе проводятся предварительные преобразования наблюдаемого ряда: фильтрация от шумов, численное дифференцирование или интегрирование и т.п. Это, в основном, технический этап численных расчетов, но и здесь нужно сделать выбор принципа расчета параметров и методики для его реализации.

Выбор приходится делать и в финале, приступая к проверке «качества» модели. Обычно качество модели проверяется с использованием прибереженной для этой цели тестовой части ряда. Проводится проверка эффективности модели для достижения требуемой точности прогноза [11]. Если модель признана удовлетворительной (эффективной), полученная конструкция берется в дело, иначе – возвращается на доработку на любой из этапов представленных на рис. 1.

На рис. 2 представлена функциональная схема системы прогнозирования погодных условий.

Рисунок 2 – Функциональная схема системы прогнозирования погодных условий
(анимация: объем - 28,1 КБ; размер - 580x179; количество кадров - 5; бесконечное число циклов повторения; задержка между кадрами - 1,3 мс; задержка между последним и первым кадром - 1,3 мс)

К настоящему времени выполнены следующие этапы:

• изучены наблюдаемые переменные, налажен их сбор с локальной метеостанции, установленной в ДонНТУ;
• собранные временные ряды метеовеличин систематизированы и подготовлены к анализу;
• проведен визуальный, спектральный, статистический анализ данных, а также анализ их взаимной зависимости;
• проведена попытка определения аргументов функций модели методом ложных соседей.

На очереди – реализация следующих:

• реконструкция модели прогноза погоды, на основании проведенных исследований и ее оптимизация;
• формирование методики расчета краткосрочного прогноза погоды;
• создание программного обеспечения, реализующего обработку и анализ временных рядов метеовеличин, динамическое определение аргументов функций и настройку параметров модели, выдачу краткосрочного прогноза погоды заданной заблаговременности.

Заключение

Итак, результатом магистерской работы должна стать методика краткосрочного прогноза погоды по временным рядам метеопараметоров, а также ее программная реализация. Данные исследования и вычисления могут стать полезными для метеорологов и быть использованы для дальнейших исследований и усовершенствований в этой области.

При написании данного автореферата магистерская работа еще не завершена. Окончательная готовность работы – декабрь 2009 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Литература

1. Кому и зачем нужен прогноз? Статья. Источник: http://www.primpogoda.ru/articles/prosto_o_pogode/komu_i_zachem_nuzhen_prognoz/
2. Гриценко А.В. Использование локальных метеостанций для прогноза погоды. Метеокомплекс VANTAGE PRO 2. – Охрана окружающей среды и рациональное использование природных ресурсов 2009 / Материалы VIII международной научной конференции аспирантов и студентов. – Донецк, ДонНТУ – 2009.
3. Немного истории о метеорологии. Статья. Источник: http://www.primpogoda.ru/articles/prosto_o_pogode/o_meteorologii/
4. Дымников В.П., Филатов А.Н. Основы математической теории климата, М.: ВИНИТИ, 1994.- 254 с.
5. Гордин В.А. Математика, компьютер, прогноз погоды. Л.: Гидромтеоиздат, 1991.
6. Rossby C.G. Relations between variations in the intensity of the zonal circulation of the atmosphere and the displacements of the semipermanent centers of actions, J. Mar. Res., 1939, v. 2, pp. 38-55.
7. Безручко Б.П., Смирнов Д.А. Математическое моделирование и хаотические временные ряды. Саратов: ГосУНЦ «Колледж», 2005. – 320 с.
8. Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. М.: Эдиториал УРСС, 2000. 336 с.
9. Горбань А.Н. Функции многих переменных и нейронные сети // Соросовский образовательный журнал. 1998. № 12. С. 105-112.
10. Заенцев И.В. Нейронные сети: основные модели. Воронеж, 1999. 76 с.
11. Гриценко А.В. Прогнозирование метеопараметров по временным рядам. – Компьютерный мониторинг и информационные технологии 2008 / Материалы IV международной научной конференции студентов, аспирантов и молодых ученых. – Донецк, ДонНТУ – 2009.