Автореферат

кваліфікаційної роботи магістра

"Прогнозування погодних умов за часовими рядами метеорологiчних показникiв"

Вступ, обґрунтування актуальності

Відомий вислів «про погоду поговорити кожен любить…» відображає той великий інтерес, який проявляє людина до навколишнього середовища. Цей інтерес зачіпає і окремих людей, і їх спільноти, і нації, і людське суспільство в цілому. Щодобове зведення погоди, наприклад, примушує людину приймати різні рішення: чи брати йому парасольку, чи займатися пошуком притулку від урагану, що насувається.

У розвинутих країнах погода та клімат давно стали категоріями економічними. Кожного року у світі стихійні нещастя забирають близько 250 000 людських життів, розмір збитків, які наносяться майну, лежить у межах 50-100 млрд. американських доларів. Але світова статистика показує: якщо довіряти гідрометеорологічній інформації та адекватно на неї реагувати, то можна відвернути від 30 до 40% втрат і повністю уникнути людських жертв [1].

Особливо помітний економічний ефект дає використання метеорологічної інформації в авіації, енергетиці, будівництві, риболовстві та судноплавстві, сільському господарстві.

Передбачення погоди з наукової точки зору – одне з найскладніших завдань фізики атмосфери. Існують різні методи для прогнозування метеорологічних явищ і їх величин, наприклад, синоптичні, кількісні, статистичні методи, але в повному об’ємі жоден метод не забезпечує поки що точного прогнозу. Саме цьому дослідження у сфері прогнозування погодних явищ є важливими і корисними, а тема – актуальною.

Мета та завдання

Мета дипломної роботи – вивчення можливості прогнозування метеопараметрів за їх часовими рядами, та, в ідеалі, формування й обробка на їх основі методики розрахунку короткострокового прогнозу погоди. Такі часові ряди представляються, зокрема, автоматизованими метеостанціями типу Vantage Pro 2 [2]. Одна з таких встановлена на факультеті обчислювальної техніки та інформатики ДонНТУ.

Ідея роботи полягає в аналізі та використанні часових рядів метеовеличин для створення моделі прогнозу погоди, адаптованої під Донецький регіон.

Завдання, які вирішуються в магістерській роботі:

• вивчення літературних джерел за методами прогнозування за часовими рядами;
• збір та аналіз метеоданих для встановлення статистичних закономірностей;
• розробка математичної прогностичної моделі;
• розробка системи прогнозування, оцінка її адекватності.

Об’єктом дослідження є система метеорологічних показників міста.

Предметом дослідження є моделі прогнозування погоди.

Методи дослідження – візуальний, статистичний та спектральний аналіз даних, метод неправильних сусідів визначення аргументів модельних функцій, методи апроксимації функцій багатьох змінних за допомогою узагальнених багаточленів, радіальних базисних функцій, штучних нейронних мереж тощо.

Наукова новизна

Наукова новизна досліджень полягає в:

• формуванні методики розрахунку короткострокового прогнозу погоди за часовими рядами метеовеличин;
• розробці програмного забезпечення, що реалізує цю методику.

Огляд досліджень та розробок за темою

Ще на початку своєї історії людина стикалася з несприятливими атмосферними явищами. Не розуміючи їх, вона обожнювала грозні та стихійні явища, пов’язані з атмосферою (боги – Перун, Зевс, Дажбог тощо). По мірі розвитку цивілізації в Китаї, Індії, країнах Середземномор’я робляться спроби регулярних метеорологічних спостережень, з’являються перші наукові уявлення про клімат. Перша праця про атмоферні явища був складений Аристотелем. Сучасна наукова метеорологія бере свій початок з XVII ст., коли були закладені основи фізики. Великим вченим Галілеєм та його учнями були винайдені термометр (1610р.), барометр, дощомір тобто з’явилась нова можливість інструментальних спостережень. Починаючи з середини XVII сторіття академія експериментування в Тоскані організовала першу небагаточисельну мережу інструментальних спостережень, які проводилися в декількох пунктах Європи. Крім цього, невід’ємною чатиною програм усіх морських плавань було проведення спостережень за погодою.

У цей час з’явилися перші метеорологічні теорії. Е. Галлей дав перше пояснення мусонів, а Е. Гадлей опубліковав трактат про пасатів. До середини XVIII в. М. В. Ломоносов вважав метеорологію самостійною наукою, головноим завданням якої було «передбачення погоди». Було організовано за приватною ініціативою Мангеймське метеорологічне товариство, яке сворило в Європі на добровільній основі мережу з 39 метеорологічних станцій (у тому числі три в Росії – Санкт-Петербурзі, Москві, Пишменський завод), укомплектованих однаковими та проградуйованими приборами. Мережа функціонувала 12 років.

У середині XIX ст. з’являються державні мережі станцій. А на початку століття працями А. Гумбольта і г. Дове у Германії закладаються основи кліматології. Близько 1820 року Г. В. Брандесу у Германії прийшла думка нанести на географічні карти спостереження Мангеймської мережі станцій. Таким чином, з’явились перші синоптичні карти, які дозволили виявити області високого та низького тиску. Вони виявилися рухомими і рухались, як правило, із заходу на схід. Після винайдення теелграфу, з 50-х років, за ініціативою астронома У. Леверьє у Франції та адмірала р. Фіцроя в Англії синоптичний метод досліджень атмосферних фронтів швидко увійшов у масове використання. На його основі виникла нова гілка метеорології – синоптична метеорологія.

До середини XIX в. відноситься организація перших метеорологічних існтитутів, у тому числі Головної фізичної обсерваторії в Петербурзі (1849р.). У другій половині XIX століття були закладені основи динамічної метеорлогії, тобто застосування законів гідромеханіки та термоденаміки до досліджень атмосферних процесів. Великий вклад у цю сферу метерології був зроблений Кориолісом та Пуасоном у Франції, В. Ферелем в Америці, Г. Гельмгольцем у Германії, Г. Моном і К. Гульдбергом у Норвегії. До кінця століття посилилося вивчення радіаційних та електричних процесів в атмосфері [3].

Розвиток метеорології в XX столітті йшов зростаючими темпами. Уперше прогноз погоди як завдання гідротермодинаміки з початковими й крайовими умовами сформулював Бьеркнес в 1904 році в доповіді на конференції в Берліні.

Спробу розв'язати таку систему рівнянь за допомогою різницевих методів здійснив під час Першої Світової війни Ричардсон. Він із групою співробітників англійської метеослужби спробував дати прогноз для району Нюренберг- Аугсбург на одну добу. Однак ця спроба виявилася невдалою - помилка в приземнім полі тиску через 6 годин склала величину порядку сотень мілібар. Ричардсон використовував нестійку різницеву схему (у той час теорії стійкості різницевих схем не існувало), і у своїх розрахунках використовував рівняння, які вимагали початкових даних для поля вітру. Ці поля він одержував з даних спостережень, одержуючи при цьому гігантську помилку в поле дивергенції, відповідальної за перетворення енергії.

Слід згадати фундаментальні роботи Карла Густава Россби [6] та Іллі Опанасовича Кибеля [7], які мали вирішальний вплив на розвиток чисельних методів прогнозу погоди. У їхніх роботах у рівняннях прогнозу погоди був виділений малий параметр, за допомогою якого можна було проводити обґрунтовані спрощення вихідних рівнянь. Наприкінці двадцятих років вийшла також робота Куранта, Фридрихса й Леви, що встановила обмеження на вибір просторових і тимчасових кроків при чисельному розв'язанні рівнянь математичної фізики [8].B 1946 році Джон ФОН Нойман зібрав невелику групу молодих учених (ведучим у цій групі був Дж.Чарни), перед якою було поставлено завдання чисельного прогнозу погоди. Перший успішний чисельний прогноз був зроблений цією групою в 1950 році [4]. Наступний принциповий крок, пов'язаний з формулюванням квазігеострофічного наближення, був зроблений майже одночасно Дж.Чарни та А.М. Обуховим.

У ці ж роки з'явилися перші (вони стали класичними) роботи, присвячені дослідженню стійкості по Ляпунову зонально-симетричних атмосферних потоків. Ці роботи продемонстрували, що при розумних значеннях параметрів Атмосферні потоки є нестійкими відносно малих збурювань початкових даних. Отже, після формулювання квазігеострофічного наближення постало завдання реалізації його у вигляді кількісної схеми прогнозу погоди. Такі реалізації були побудовані в 1952 році Н.І.Булеєвим та Г.І.Марчуком. Метод був заснований на побудові функції Гріна для тенденції геопотенціалу й був реалізований С.Л.Бєлоусовим у вигляді оперативної схеми прогнозу погоди в Гідрометцентрі СРСР.

Вже в ці роки вчені дійшли висновку, що нестійкість атмосферних потоків стосовно помилок початкових даних призводить до обмеження часу корисного прогнозу. Аналогічних обмежень слід було очікувати й від помилок, які містилися в спрощених рівняннях, тому на початку 60-х років була сформульована проблема створення кількісної схеми прогнозу погоди на основі повних рівнянь гідротермодинаміки атмосфери з обліком усіх значимих неадіабатичних факторів.

На перших етапах розв'язання цієї проблеми центральним завданням була розробка ефективних кількісних методів вирішення гіперболічних нелінійних рівнянь. В 1966 році вийшла робота А.Аракави, у якій він запропонував метод побудови різницевої схеми для рівнянь двовимірної нестисливої рідини, що володіє двома квадратичними інваріантами. У цьому ж році Кирк Брайєн запропонував метод кінцевих обсягів (у сучасній термінології).

У середині 60- х років Г.І.Марчук запропонував для розв'яання рівнянь гідротермодинаміки атмосфери абсолютно стійкі неявні схеми, засновані на методі розщеплення за фізичними процесами і геометричними змінними. Цей метод був покладений в основу розробленої в ОЦ ІЗ АН СРСР кількісної схеми прогнозу погоди за повними рівняннями, впровадженій потім в оперативну практику Західно-сибірського УГМС.

Довгий час спектральний метод був надбанням тільки метеорологічного наукового середовища й використовувався для розв'язання рівнянь динаміки атмосфери. В 60- х роках спектральний метод, або метод Гальоркіна, у якому в якості базисних функцій використовуються сферичні гармоніки, був не конкурентоспроможним ,у порівнянні з різницевими методами, через велику кількість арифметичних операцій і використовувався тільки в моделях малої розмірності. Однак, після відкриття Орзагом спектрально-сіткового перетворення, він посів провідне місце при конструюванні моделей прогнозу погоди й загальної циркуляції атмосфери.

Наприкінці 60- х - початку 70- х років у результаті великої серії чисельних експериментів була вироблена вистава, що межа "детермінованої" передбачуваності становить величину порядку двох тижнів (деякі оцінки давали три тижні) і на порядок денний вийшло завдання створення моделі середньострокового прогнозу погоди (1-7 днів). Базою для створення таких моделей повинні були стати обчислювальна техніка, що швидко розвивається, розвиток спостережливої мережі - більші надії покладали на супутникові спостереження й наукові розробки параметризацій процесів підсіткових масштабів, об'єктивного аналізу даних спостережень тощо. Цю програму була здійснено в створеному в 1975 році Європейському центрі середньострокових прогнозів погоди. Основним результатом цієї роботи,виконаної під керівництвом Л. Бенгтсона, була розробка високої технології - системи чотиривимірного засвоєння даних, яка дозволила вивести прогностичну систему Європейського Центру на перше місце у світі. Розв'язання цієї проблеми було можливе тільки на основі результатів Першого глобального експерименту, які дозволили визначати якість моделі - її здатність ефективно засвоювати асинхронні дані.

Першу чисельну модель загальної циркуляції атмосфери на основі квазігеострофічних рівнянь (двошарова модель) побудував Н. Филліпс [4]. На початку 60- х років Д. Смагоринський, очоливши знову утворену в Прінстоні Лабораторію геофізичної гідродинаміки, сформулював програму послідовного вивчення ролі різних неадіабатичних факторів у формуванні загальної циркуляції атмосфери за допомогою чисельних моделей, заснованих на повних рівняннях гідротермодинаміки.

Одночасно почалася розробка моделей загальної циркуляції океану, і на основі цих моделей спільної моделі загальної циркуляції атмосфери й океану, яка повинна була стати основою глобальної кліматичної моделі. У Радянському Союзі така програма була сформульована на початку 70- х років в Обчислювальному центрі СО АН СРСР (Г.І.Марчук) і успішно реалізовувалася протягом наступних 20 років спочатку в ОЦ, а потім в Інституті обчислювальної математики РАН. Паралельно велика увага також приділялася проблемі прогнозу змін клімату під впливом антропогенної діяльності людини, зокрема, під впливом збільшення концентрації вуглекислого газу в атмосфері.

Великий внесок зробила група співробітників уже згаданої Лабораторії геофізичної гідродинаміки, керована Суки Манабе. Ними була висвітлена фундаментальна проблема в теорії клімату - проблема чутливості клімату до малих зовнішніх впливів і формалізована на основі теорії диссипативных динамічних систем. В 90-хе роках в Інституті обчислювальної математики РАН під керівництвом В.П.Димнікова [6] було виконано формулювання методів побудови операторів відгуку кліматичної системи на малі зовнішні впливи. Ключовим моментом цього підходу було дослідження структури аттракторів кліматичних моделей і їх стійкості.

Слід підкреслити, що розвиток моделей прогнозу погоди й клімату прямо стимулювався розвитком обчислювальної техніки. Три революції в обчислювальній техніці, які відбулися в останні 30 років - перехід на інтегральні схеми, створення машин з конвеєрними обчисленнями й створення паралельних обчислювальних систем зі швидкою комунікацією призвели до розробки високих обчислювальних та інформаційних технологій у проблемі прогнозу погоди. В основі цих технологій лежать методи розв'язання трьох завдань - безпосередньо завдання прогнозу погоди, завдання ініціалізації початкових даних (ліквідація шоку гравітаційних хвиль у початковий момент часу) і завдання чотиривимірного засвоєння даних. Розв'язання проблеми передбачуваності шукається за допомогою використання в початковий момент часу деякого розподілу помилок початкових даних, тобто розв'язання не одного, а серії прогностичних завдань. Цей метод ідеально лягає на структуру паралельних обчислювальних систем.

Апробація

Результати роботи доповідалися на V міжнародній конференції студентів, аспірантів та молодих вчених «Комп’ютерний моніторинг та інформаційні технології» (КМІТ-2009) і опубліковані у відповідному збірнику.

Поточні та заплановані результати

Не дивлячись на безмежну кількість ситуацій, об’єктів та цілей, які вносять у процес своє специфічне, можна виділити основні етапи моделювання і представити їх у вигляді схеми (рис. 1). Робота починається з розгляду наявної інформації про проект (експериментальних даних про нього самого або подібних об’єктах; теорій, розроблених для описання класу об’єктів, що досліджуються; інтуїтивних представлень тощо) з позиції мети дослідження, з отримання та попереднього аналізу рядів величин, які спостерігаються, а закінчується використанням отриманої моделі для вирішення конкретного завдання. Але цей процес, як правило, є ітераційним – супроводжується неодноразовими повтореннями, поверненнями на вихідну та проміжну точки схеми, послідовними наближеннями до «гарної» моделі.

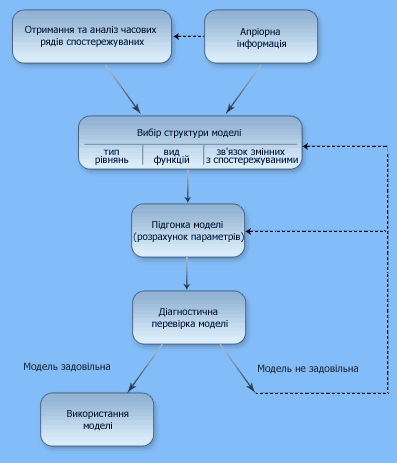
Рисунок 1 - Типова схема процесу емпіричного моделювання

Розглянемо більш детально кожний етап.

На першому етапі здійснюється отримання даних та їх систематизація. Далі застосовується один або декілька методів аналізу наявних тимчасових рядів метеовеличин, що спостерігаються. Це, наприклад, візуальний аналіз у вигляді графіків залежності змінної від часу, відновлення фазової траєкторії, спектральний та статистичний аналіз тощо [7].

На ключовому в схемі етапі 2 формується структура моделі. Першочергово обирається тип рівнянь, далі задається вид вхідних у них функцій, після чого встановлюється зв'язок динамічних змінних (компонент вектору x) із величинами a. В якості змінних можуть виступати власне спостережувані, але у більш загальному випадку цей зв'язок задають у вигляді a = h(x) , де h називають вимірювальною функцією. Часто вводять ще випадковий додаток e: a = h(x) + e, щоб урахувати вимірювальний шум. Щоб зробити модель більш реалістичною, випадковий додаток вводять нерідко і власне у рівняння – так званий динамічний шум.

Формування структури моделі – найбільш складний і творчий етап процедури моделювання. На даному етапі обирається тип рівняння, вид вхідних у них функцій та їх аргументів.

Завдання визначення аргументів функції полягає в тому, щоб визначити найменшу розмірність моделі, яка забезпечує однозначність прогнозу. Для вирішення цього завдання використовуються різні методи оцінки: метод неправильних сусідів, метод головних компонент, метод Грассбергера-Прокаччиа, метод гарно пристосованого базису. Перший з них полягає в наступному.

Він заснований на перевірці тієї властивості, що фазова траєкторія, яка була відновлена у просторі достатньої розмірності. Не повинна мати самоперетинань. За умови пробної розмірності D для кожного відновленого вектору x_k відшукують одного (найближчого) сусіда; збільшивши D на 1, визначають які з сусідів виявилися неправильними (суттєво розійшлися), а які – справжніми. Підраховують відношення кількості неправильних сусідів до загальної кількості відновлених векторів. Якщо під час збільшення D ця кількість стає малою за умови деякого значення D*, то останнє і є оцінкою розмірності простору, в якому досягається вкладання траєкторії модельованого руху [7].

Далі іде етап визначення структури модельних рівнянь. Для цього використовуються різні методи апроксимації функцій багатьох змінних: метод узагальненого багаточлена, використання радіальних базисних функцій, штучні нейронні сітки, локальні моделі, пошук близьких сусідів.

Розглянемо деякі з них.

1) Метод узагальнено багаточлена.

Для побудови глобальної моделі обирають вид f і розраховують параметри звичайним МНК, тобто вимагають, щоб

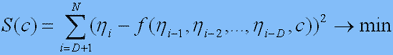(1)

Для простоти розрахунків бажано обирати функцію f, лінійну по відношенню до c. Це має місце для так званого узагальненого багаточлена за деякою системою базисних функцій f₁,f₂,...,f_p:

(2)

При цьому завдання (1) лінейне і не виникає проблеми локальних мінімумів. До такого способу відноситься використання алгебраїчного багаточлена, порядок якого збільшується, поки не буду віднайдена адекватна модель.

2) Радіальні базисні функції.

Це функції виду ф_k(x)=ф(||x-a_k||/r_k), де ||·|| означає норму (довжину) вектора. В якості «материнської» функції ф звичайно береться як слід локалізована функція, наприклад, «гауссиана» ф(y)=exp(-y²/2), величини a_k називають «центрами», а r_k – «радіусами». Модельна функція f представляє собою узагальнений багаточлен за системою функцій:

.

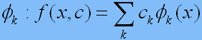Кожен доданок суттєво відмінний від нуля тільки на відстані, не більшій r_k від центру a_k. Інтуїтивно зрозуміло, що за допомогою такої суперпозиції можна наблизити достатньо складний рельєф.

3) Штучні нейронні сітки (ШНС).

Моделі з ШНС широко та успішно використовуються для вирішення багатьох завдань. Вони представляють із себе не суму базисних функцій, а їх композицію. На відміну від узагальненого багаточлена, вони обов’язково нелінійно залежать від параметрів, що оцінюються.

Опишемо ШНС формально на прикладі багатошарового персептрону. Нехай x=(x₁,...,x_p) – аргумент шуканої функції f. Складемо набір функцій: f_j⁽¹⁾(x), j=1,...,K₁:

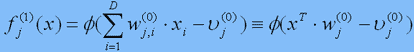(3)

де постійні w_j,i⁽⁰⁾ называють вагами, u_j⁽⁰⁾ – порогами, ф – функцією активації. Функція ф звичайно нелінійна и має графік східчастого виду. Кожна функція f_j⁽¹⁾ представляє вихід стандартного формального нейрону з номером j, на вхід якого поданий вектор x. Система функцій f₁⁽¹⁾,...,f_k1⁽¹⁾ – це набір нейронів першого шару. Назвемо значення функцій f_j⁽¹⁾ вихідними значеннями нейронів першого шару і позначимо їх сукупність вектором y⁽¹⁾ з компонентами y_j⁽¹⁾=f_j⁽¹⁾(x).

Визначимо в якості функції f лінійну комбінацію f₁⁽¹⁾, отримаємо так звану одношарову ШНС:

,

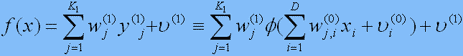де параметри w_j⁽¹⁾,u⁽¹⁾ – додаткові ваги та поріг.

Вільних параметрів у такій моделі P=K₁(D+1)+(K₁+1) штук. Це уявлення схоже на узагальнений багаточлен (2), але ШНС нелінійно залежить від параметрів w_j,i⁽⁰⁾ и u_i⁽⁰⁾.

Розглянемо тепер ще одну систему функцій f_j⁽²⁾, j=1,...,K₂, які мають вид (3), але залежать від K₁-мерного аргументу. Це нейрони другого шару, на вхід яких подаються виходи нейронів першого шару y⁽¹⁾. Окреслимо їх вихідні значення вектором y⁽²⁾ розмірності K₂ і визначимо функцію f як лінійну комбінацію вихідних значень нейронів другого шару:

.

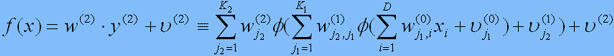Це двошарова ШНС, який містить уже наразі композиції функцій, які суттєво відрізняють її від псевдолінійної моделі (2). Збільшення кількості шарів досягається очевидним чином.

Частіше за все для вирішення завдань апроксимації використовують двошарові ШНС, рідше – тришарові [8]. Збільшення кількості шарів не призводить до суттєвого покращення. Покращення досягають за рахунок збільшення кількості нейронів у шарах K₁,K₂. Теоретична основа використання ШНС – узагальнена апроксимаційна теорема (її окремим випадком є теорема Вейерштраса), яка стверджує, що будь-яка безперервна функція може бути скільки завгодно точно рівномірно наближена за допомогою ШНС [9].

Процедура розрахунку параметрів ШНС шляхом мінімізації – її «навчання» - це складне завдання багатомірної нелінійної оптимізації, для вирішення якої розвинуті спеціальні «технології»: алгоритм зворотного розповсюдження помилки, навчання з шумом, стохастична оптимізація (генетичні методи метод імітації віджигу) [10]. ШНС може містити дуже багато зайвих елементів, та структуру цієї моделі (архітектуру сітки) бажано зробити компактніше. Для цього нейрони, важелі та пороги яких слабко змінюються в процесі навчання, виключаються з сітки.

Якщо наявні декілька альтернативних ШНС з різною архітектурою, отриманні в результаті навчання за тренувальним рядом, то кращу з них звичайно обирають за найменшою тестовою помилкою апроксимації. Для отримання «чесного» показника прогностичної ефективності моделі використовують ще один ряд (не тренувальний і не тестовий, оскільки вони обидва використовувались для побудови моделі), який називають «екзаменаційним».

Після вибору структури виконують «підгонку моделі». Для цього, як правило, проводиться пошук екстремального значення деякої цільової функції, наприклад, мінімізується сума квадратів відхилень вирішення модельних рівнянь від даних, що спостерігаються. За необхідності на даному етапі проводяться попередні перетворення ряду, за яким спостерігають: фільтрація від шумів, кількісне диференціювання або інтегрування тощо. Це, в основному, технічний етап кількісних розрахунків, але і в цьому випадку потрібно зробити вибір принципу розрахунку параметрів та методики для його реалізації.

Вибір доводиться робити і в фіналі, приступаючи до перевірки «якості» моделі. Як правило, якість моделі перевіряється з використанням тестової частини ряду, яка прибережена для цієї мети. Проводиться перевірка ефективності моделі для досягнення потрібної точності прогнозу [11]. Якщо модель визнана задовільною (ефективною), отримана конструкція береться у справу, в іншому випадку – повертається на допрацювання на будь-який з етапів, що представлені на рис. 1 [1].

На рис. 2 представлена функціональна схема системи прогнозування погодних умов.

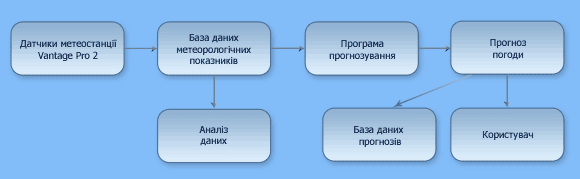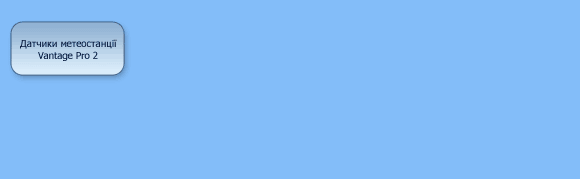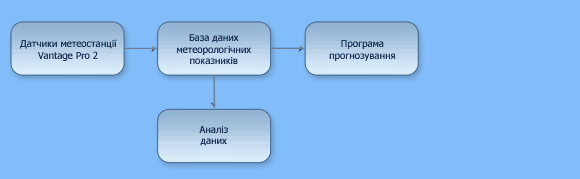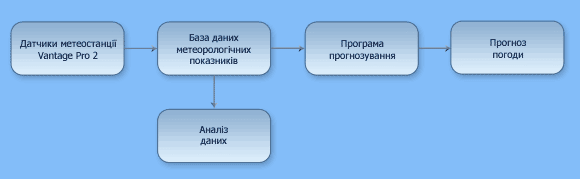
Рисунок 2 – Функціональна схема системи прогнозування погодних умов
(анімація: обсяг - 28, 1 КБ; розмір - 580х179; кількість кадрів - 5; безкінечна кількість циклів повторення; затримка між кадрами - 1, 3 мс; затримка між останнім та першим кадром - 1, 3 мс)

На даний час виконано наступні етапи:

• вивчені змінні, які досліджуються, налагоджений їхній збір з локальної метеостанції, встановленої в ДонНТУ;
• зібрані тимчасові ряди метеовеличин систематизовані та підготовані до аналізу;
• проведено візуальний, спектральний, статистичний аналіз даних, а також аналіз їх взаємозалежності;
• проведено спробу визначення аргументів функцій моделі методом помилкових сусідів.

На черзі – реалізація наступних:

• реконструкція моделі прогнозу погоди, на основі проведених досліджень та її оптимізація;
• формування методики розрахунку короткострокового прогнозу погоди;
• створення програмного забезпечення, яке реалізує обробку та аналіз тимчасових рядів метеовеличин, динамічне визначення аргументів функцій та налаштування параметрів моделі, видачу короткострокового прогнозу погоди встановленої завчасності.

Висновок

Отже, результатом магістерської роботи повинна стати методика короткострокового прогнозу погоди за тимчасовими рядами метеопараметрів, а також її програмна реалізація. Дані дослідження і розрахунки можуть стати корисними для метеорологів і бути використані для подальших досліджень та вдосконалень у цій сфері.

Під час написання даного автореферату магістерську роботу ще не закінчено. Остаточна готовність роботи – грудень 2009 року. Повний текст роботи і матеріали за темою можуть бути отримані у автора або його керівника після вказаної дати.

Література

1. Кому и зачем нужен прогноз? Статья. Источник: http://www.primpogoda.ru/articles/prosto_o_pogode/komu_i_zachem_nuzhen_prognoz/
2. Гриценко А.В. Использование локальных метеостанций для прогноза погоды. Метеокомплекс VANTAGE PRO 2. – Охрана окружающей среды и рациональное использование природных ресурсов 2009 / Материалы VIII международной научной конференции аспирантов и студентов. – Донецк, ДонНТУ – 2009.
3. Немного истории о метеорологии. Статья. Источник: http://www.primpogoda.ru/articles/prosto_o_pogode/o_meteorologii/
4. Дымников В.П., Филатов А.Н. Основы математической теории климата, М.: ВИНИТИ, 1994.- 254 с.
5. Гордин В.А. Математика, компьютер, прогноз погоды. Л.: Гидромтеоиздат, 1991.
6. Rossby C.G. Relations between variations in the intensity of the zonal circulation of the atmosphere and the displacements of the semipermanent centers of actions, J. Mar. Res., 1939, v. 2, pp. 38-55.
7. Безручко Б.П., Смирнов Д.А. Математическое моделирование и хаотические временные ряды. Саратов: ГосУНЦ «Колледж», 2005. – 320 с.
8. Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. М.: Эдиториал УРСС, 2000. 336 с.
9. Горбань А.Н. Функции многих переменных и нейронные сети // Соросовский образовательный журнал. 1998. № 12. С. 105-112.
10. Заенцев И.В. Нейронные сети: основные модели. Воронеж, 1999. 76 с.
11. Гриценко А.В. Прогнозирование метеопараметров по временным рядам. – Компьютерный мониторинг и информационные технологии 2008 / Материалы IV международной научной конференции студентов, аспирантов и молодых ученых. – Донецк, ДонНТУ – 2009.