http://www.viniti.ru

Сравнительно молодое направление в сфере защиты информации, цифровая и компьютерная стеганография, будучи некогда своего рода особым искусством поиска интересных решений в сокрытии информации, отнесенным к такому флагману безопасности как криптография, к настоящему времени выделилась в отдельную ветвь, определила и уже весьма прочно закрепила свои позиции. Неоспоримым свидетельством тому являются многочисленные публикации, стабильно появляющиеся все новые и более надежные методы, алгоритмы, программные средства как самой стеганографии, так и стеганоанализа. В тоже время, обзорный анализ публикаций последних лет показал, что большинство работ посвящено либо новым методам выявления стеганографических вложений, либо же новым, более стойким стеганографическим методам сокрытия информации с использованием тех или иных носителей. Вопросы же практического применения и даже приближенной оценки надежности стеганографических систем остаются в стороне, что не позволяет стеганографии достичь широкого практического применения.

При разработке новых стеганографических методов, разработчиками в основном используются только две наиболее популярные модели стеганографического канала. Первая это классическая модель стеганографической системы, представленная на рис. 1,а которая была предложена Симмонсом [1] еще в 1984 году. Модель предполагает использование стеганографических алгоритмов, непосредственно зависящих от некоторого секретного ключа, без привлечения дополнительных криптографических алгоритмов. Ввиду высокой сложности проектирования указанных алгоритмов, большее предпочтение отдается стеганографическим системам, построенным на основе явного или неявного использования элементов криптографии, (рис.1,б). Разработчики в данном случае, говорят о криптографии как о дополнительном рубеже защиты, упуская тот факт, что для стеганографических систем связи основной угрозой является обнаружение самого факта скрытой передачи информации, а не ее извлечение и декодирование. В обоих случаях, доказать стойкость конечной стеганографической системы к атакам пассивного противника весьма сложно. В первом случае это требует четкого математического обоснования стойкости каждого из реализуемых стеганографических алгоритмов по целому ряду параметров. Во втором случае доказать стойкость системы и вовсе не представляется возможным ввиду сложности перестройки и некоторого постоянства используемых стеганографических алгоритмов, а также несогласованности криптографической и стеганографической частей системы.

Вместе с тем, среди зарубежных изданий и материалов трудов профильных конференций, все же можно выделить несколько публикаций, посвященных вопросам теоретической стойкости стеганографических систем. В частности, в работе [2] стеганографический канал рассмотрен с точки зрения теории информации. В этой работе впервые было дано определение и предложено теоретическое обоснование существования теоретически совершенной стеганографической системы, по аналогии с совершенными шифрами. Доказательство основано на использовании в качестве контейнеров псевдослучайных последовательностей с равномерным распределением и последующим их замещением данными скрываемого сообщения, также представляющими собой псевдослучайную последовательность с аналогичным распределением. Разумеется, в явном виде построение подобных стеганографических систем не представляется возможным, ввиду жесткого ограничения, как на контейнеры, так и на передаваемые сообщения. Вместе с тем аналогичные принципы могут быть положены в основу новых перспективных моделей стеганографических систем.

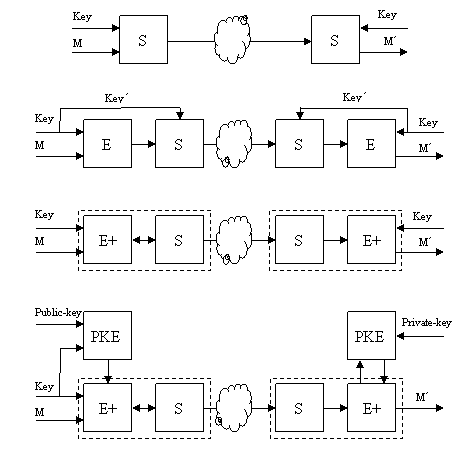
                                   Рисунок 1 - Варианты стеганографических и криптостеганографических систем

Весьма перспективным видется направление построения стеганографических систем на основе более плотного взаимодействия или же синтеза криптографии и стеганографии, когда, с одной стороны, применяются зарекомендовавшие себя криптографические алгоритмы, а с другой, отвечающие определенным требованиям и ограничениям новые стеганографические методы. Рассмотрим одно из подобных решений – криптостеганографические системы.

Криптостеганографической системой будем называть систему скрытой передачи информации на открытых каналах связи, основанную на совместном применении криптографических алгоритмов, стеганографических методов, а также алгоритмов согласования входных и выходных данных указанных алгоритмов и методов. Отличительной особенностью от стеганографических систем, построенных с применением криптографических алгоритмов (аналогичных системе представленной на рис. 1,б), является наличие жесткой связки алгоритмов криптографии и методов стеганографии, роль которой играют алгоритмы согласования.

Применение алгоритмов шифрования и согласования позволяет уйти от использования стеганографических методов, стойкость которых основана на использовании секретного ключа или на секретности самих методов. Рассмотрим этот момент немного подробнее. В общем случае, стеганографическая система может быть представлена в виде совокупности объектов S = (C, M, K, Q, H, R), каждый из которых тем или иным образом влияет на алгоритмы сокрытия и извлечения информации. Множества пустых C и заполненных Q контейнеров, остаются и в случае криптостеганографической системы. Множество скрываемых сообщений M, представляет собой уже множество, состоящее из двоичных битовых последовательностей с распределениями аналогичными распределениям двоичных последовательностей, извлекаемым из пустых контейнеров. Так как ключи в криптостеганографической системе используются только криптографической частью, множество ключей K можно считать пустым. А раз используются безключевые алгоритмы встраивания и извлечения информации, то множества правил внедрения H и извлечения сообщений R из контейнеров становятся одноэлементными: H = {h}, R = {r}. В результате используемая в криптостеганографических системах стеганографическая часть представима в виде S = (C, M, Q, h, r). Отсутствие лишних элементов, меньшая неопределенность относительно скрываемых данных и применение безключевых правил внедрения/извлечения информации позволяет применять значительно более простые стеганографические алгоритмы, которые в тоже время должны отвечать ряду требований:

- стеганографический алгоритм должен извлекать сообщения как из заполненных, так и из пустых контейнеров, при этом вероятность извлечения сообщения не должна зависеть от выбранного контейнера: " m = r(c): c Î C È Q | m Î M, p(m) = 1/|M|;

- извлекаемые и записываемые сообщения должны представлять собой битовые строки конечной длины с p0 > 0, p1 > 0;

- запись сообщения в контейнер должна осуществляться путем замены исходно содержавшегося в нем сообщения, а не путем внесения в контейнер дополнительной информации, H(q) » H(c), где H – функция оценки количества информации в сообщении;

- заполненный контейнер должен сохранять свою функциональность и обладать свойством естественности, т.е. "q = h(c, m) : c Î C, m Î M | q Î C (Q Í C);

- процесс записи данных нового сообщения должен учитывать структуру контейнера и существующие корреляционные связи между элементами контейнера;

- стеганографический алгоритм должен быть e совершенным практически в смысле работы [3] с e > 0.

Рассмотрим общую математическую модель криптографических систем [4], представляющую собой совокупность S = (X, K, Y, E, D) объектов, где X – множество открытых текстов, Y – множество зашифрованных сообщений, множество ключей – K = {0, 1, … n-1}, E – множество правил зашифрования на ключах из K, D – множество правил расшифрования. Наибольший интерес для нас представляет множество зашифрованных сообщений Y. Так шифрование изменяет статистические характеристики сообщений, повышая их энтропию и делая более похожими на случайные данные, с распределением близким к равномерному. Тут скрывается очень важный момент, в действительности, для современных шифров отличить зашифрованное сообщение от случайной последовательности символов с равномерным распределением является если и не неразрешимой, то весьма сложной задачей. Другой важный момент связан с множеством ключей K и множеством правил расшифрования D, заключается в том, что при попытке расшифровать некоторый элемент y Î Y без знания конкретного ключа мы получим целое множество равновероятных вариантов исходного сообщения. Соответственно определить, что перед нами именно зашифрованное сообщение, а не случайный набор символов, представляется возможным только в том случае, если нам известен верный ключ расшифрования. Таким образом, с одной стороны, применение криптографических алгоритмов позволяет свести множество всех сообщений с различными характерами распределений к множеству равновероятных сообщений с равномерным распределением, с другой – знание ключа расшифрования позволяет нам различить зашифрованное сообщение от просто случайного набора символов.

В криптостеганографических системах равномерное распределение на множестве зашифрованных сообщений следует считать основным требованием к применяемым криптографическим алгоритмам.

Криптостеганографическая система представляет собой сложный комплекс, общая стойкость которого не определяется лишь только стойкостью используемого скрывающего преобразования. Большую роль для надежности системы играет правильное согласование криптографической и стеганографической частей системы. Так, далеко не всегда извлеченная из контейнера битовая последовательность будет соответствовать по своему характеру случайной последовательности с равномерным или нормальным распределением. Роль связующих функций в данном случае играют согласующие алгоритмы, позволяющие из равномерно распределенной битовой последовательности y Î Y, получить последовательность с заданным, произвольным распределением m Î M.

Рассмотрим простой пример подобных согласующих функций. Пусть у нас дана битовая последовательность y = 011011001… и битовая последовательность m = 000111100110100100000010000100000111111…, попробуем построить битовую последовательность mў близкую по своим статистическим характеристикам к последовательности m, но при этом содержащую в себе данные сообщения y.

Для последовательности m перейдем к новому алфавиту F = {a, b, c, d}, и зададим биективное отображение f : {00, 01, 10, 11} ® F, согласно простому правилу: a « "00", b « "01", c « "10", d « "11". Сообщение m примет следующий вид: m = a b d c b c c b a a a c a b a a b d d c…

Выше говорилось о том, что исходная битовая последовательность также содержит сообщение, попробуем извлечь исходное сообщение. Для этого символы b и c нового алфавита поставим в соответствие символам двоичного алфавита {0, 1}: b « "0" , c « "1", символы a и d заменим пустым символом. Тогда из последовательности m можно будет извлечь сообщение: y* = 0101101001…

Заменим имеющееся сообщение y* сообщением y. Для этого также перейдем к алфавиту {b, c}: y = b c c b c c b b c…

В сообщении m последовательно заменим символы b, с, символами из y:

m' = a b d c c b c c a a a b a b a a c d d c…

и перейдем обратно к алфавиту {00, 01, 10, 11}:

m' = 0001111010011010000000010001000010111110…

Как видно из примера, полученная последовательность сохранила длинные последовательности нулей и единиц, а также их соотношение. Таким образом, может быть осуществлен перевод равномерно распределенных битовых строк полученных на выходе алгоритмов шифрования, в битовые строки аналогичные извлекаемым стеганографическими алгоритмами из пустых контейнеров. Более совершенные и рекомендуемые к использованию на практике алгоритмы согласования представлены в [5]. Основным требованием, предъявляемым к алгоритмам согласования, применяемым в криптостеганографических системах, является точное статистическое соответствие входных и выходных данных, входным и выходным данным криптографической и стеганографической частей системы.

В общем случае процесс записи информации в контейнер в криптостеганографической системе содержит следующие основные шаги:

1. Из обрабатываемого контейнера c Î C извлекается битовая строка m Î M.

2. Оценивается объем данных, которые можно записать в полученную битовую строку m, с учетом ограничений, накладываемых стеганографическим алгоритмом встраивания сообщений.

3. Производиться предварительная подготовка предназначенных для передачи данных, в ходе которой данные сжимаются и при необходимости, разбиваются на блоки, далее к ним добавляется заголовок, контрольная сумма, накладывается код коррекции ошибок.

4. Прошедшие предварительную подготовку данные подвергаются процедуре шифрования, для получения битовой последовательности y Î Y с равномерным распределением.

5. Алгоритмами совмещения осуществляется сведение строк, полученных на шагах 1 и 4 битовых строк m' = g(m, y).

6. Полученная на шаге 5 битовая строка m' записывается в исходный контейнер взамен строки m, с учетом существующих в контейнере корреляционных связей и вносимых при записи искажений.

При извлечении сообщения из контейнера в качестве некоторого индикатора, что извлечено именно сообщение, а не мусор, может служить контрольная сумма сообщения и записанный в начале заголовок сообщения. Отметим, что контрольная сумма, заголовок сообщения, равно как и сами данные сообщения оказываются доступными только на выходе криптографической части системы, при условии верного задания ключа расшифрования сообщения. Если ключ расшифрования задан неверно, то на выходе как из заполненного, так и из пустого контейнеров может быть получено совершенно произвольное сообщение. Таким образом, выполняется одно из главных требований предъявляемых к стойким стеганографическим системам – пустой контейнер тоже содержит в себе сообщение.

В заключение отметим, что криптостеганографические системы могут быть построены как на основе использования симметричных криптосистем, (рис.1,в), так и на основе ассиметричных криптосистем, в которых алгоритмы ассиметричной криптографии используются для целей передачи секретного сеансового ключа совместно с передаваемым сообщением. В этом случае, шифрование данных сообщения осуществляется средствами симметричных алгоритмов шифрования, а для шифрования данных симметричного ключа используются алгоритмы шифрования на открытых ключах. Соответствующая модель криптостеганографической системы на основе открытых ключей представлена на (рис.1,г). Все предложенные модели прошли апробацию при построении реальных систем.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Simmons G.J., "The Prisoners' Problem and Subliminal Channel", in Advances in Cryptology, Proceedings of CRYPTO '83, Plenum Press, 1984, pp. 51-67.

2. Christian Cachin, An Information-Theoretic Model for Steganography, In Proceeding of 2nd Workshop on Information Hiding (D. Aucsmith, ed.), Lecture Notes in Computer Science, Springer, 1525, pp. 306-318, 1998.

3. Алиев А.Т., Балакин А.В. Оценка стойкости систем скрытой передачи информации // Известия ТРТУ. Тематический выпуск. Материалы VII Международной научно-практической конференции "Информационная безопасность". – Таганрог: Изд-во ТРТУ, 2005. №4 (48), – С. 199-204.

4. Зубов А.Ю. Совершенные шифры. – М.: Гелиос АРВ, 2003. –160 с.

5. Алиев А.Т., Способ внедрения дополнительной информации в цифровые изображения, Патент РФ: №2288544 от 24.12.2004.