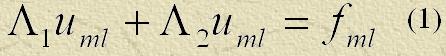
В настоящее время одной из сложнейших задач в мире считается решение ресурсоемких задач. Если возникает необходимость в решении сложной вычислительной проблемы, например, решение системы из 1000 уравнений, проведении связанных с ней расчетов, сравнений и сортировок, то ни кластеры балансировки нагрузки, ни кластеры высокой доступности здесь не помогут. Для решения подобных ресурсоемких задач применяется отдельный тип кластеров, который называют вычислительным или академическим.
Вычислительные кластеры (High Performance Computing Cluster) обеспечивают повышение производительности целевых приложений, если функции этих приложений — ресурсоемкие вычисления. Рост производительности напрямую связан с распределением одного вычислительного процесса по всем доступным узлам кластера.
Свою версию кластера в 2005 году выпустила компания Microsoft. Этот продукт получил название Microsoft Windows Compute Cluster Server 2003 (WCCS 2003).Технологически Microsoft Windows Compute Cluster Server 2003 [8] базируется на стандартной версии Microsoft Windows Server 2003. В поставку продукта входят: модифицированная версия Windows Server 2003 x64 Standard Edition и пакет, называемый Compute Cluster Pack.
Модифицированная версия Windows Server 2003 позволяет существенно снизить стоимость конечного узла, поскольку ограничивает возможность работы только в роли узла вычислительного кластера. Компоненты, входящие в Compute Cluster Pack [8], — это набор сервисов, утилит и протоколов. Этот набор представляет собой роль «вычислительный кластер» для установки на базовую операционную систему. Для специально разработанных вычислительных задач пользователи могут применять стандартную поставку WCCS 2003.
Встроенным средством программирования на кластере является MS MPI. Message Passing Interface (MPI) — один из стандартов разработки приложений HPC.
В задачи MPI входит создание набора процессов и их сессий, обеспечение передачи данных и сигналов между ними для разделения кода приложения на потоки согласно имеющимся вычислительным ресурсам с целью достижения максимальной производительности.
Исследование параллельного многосеточного метода Федоренко на вычислительном кластере Microsoft Windows Compute Cluster Server 2003 актуально, так как такие исследования еще не проводились.
Целью работы является разработка и реализация программной системы, позволяющей получить решение дифференциальных уравнений в частных производных многосеточным методом на вычислительном кластере.
Главными задачами исследований является:
Предметом исследований являются технологии параллельного решения уравнений в частных производных на вычислительном кластере Microsoft Windows Compute Cluster Server 2003 с применением многосеточных методов.
Данные исследования выполняются впервые в указанных условиях.
Использование программной системы позволит оценить быстродействие и точность решения дифференциальных уравнений параллельным методом на вычислительном кластере. Программная система может быть использована для параллельного решения дифференциальных уравнений в частных производных многосеточным методом.
По результатам выполненных исследований автором сделан доклад, на международной научно-технической конференции "Информатика и компьютерные технологии" 12-15 мая 2009 состоявшейся в г. Донецке в стенах Донецкого Национального Технического Университета
Дифференциальные уравнения в частных производных представляют собой широко применяемый математический аппарат при разработке моделей в самых разных областях науки и техники.
Как известно, явное решение этих уравнений в аналитическом виде оказывается возможным только в частных простых случаях. Поэтому основная возможность анализа математических моделей, построенных на основе дифференциальных уравнений, обеспечиваются при помощи приближенных численных методов решения. Объем выполняемых при этом вычислений является значительным. Поэтому необходимым является использование высокопроизводительных вычислительных систем для данной области вычислительной математики. В настоящее время проблематика численного решения дифференциальных уравнений в частных производных является предметом интенсивных исследований.
Одним из наиболее эффективных подходов к решению дифференциальных уравнений в частных производных является многосеточный подход. Главной особенностью является то, что решение производится сначала на грубой(крупной) сетке, а затем переносится на более мелкую сетку. Начальное решение для сетки NxN, где N – количество узлов, строится посредством аппроксимирующей сетки (N/2)x(N/2), получаемой сохранением каждого второго узла исходной сетки NxN. Более грубая сетка (N/2)х(N/2), в свою очередь, аппроксимируется сеткой (N/4)х(N/4) и так далее. Затем в частной области погрешность представляется как сумма синусоид с различными частотами. Тогда работа, выполняемая на конкретной сетке, уменьшает половину частотных компонент погрешности, для которых уменьшение не было достигнуто на более грубых сетках. Поэтому работа, производимая для усреднения решения в каждом узле сетки, делает приближенное решение глаже, что эквивалентно подавлению высокочастотных компонент погрешности.
Приближенный алгоритм решения рассмотрим на сеточном уравнении Пуассона:
Рассмотрим сеточное уравнение Пуассона на пятиточечном шаблоне разностной схемы "крест"[10]:
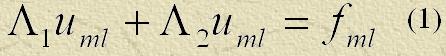
и, кроме того, уравнение
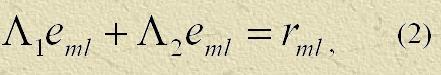
где
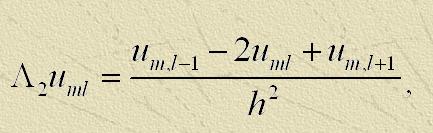
h – шаг по координатам,
u – искомое решение,
u' – приближенное решение (1),
r — невязка,
e — погрешность решения.
Если известно приближенное решение первой задачи, то, решая вторую, можно найти решение исходной системы по формуле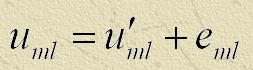 
,
но решение задачи (2) по сложности точно такое же, как и решение исходной задачи.
Если применять итерационный метод к первому уравнению, сделав несколько итераций, то приближенное решение задачи будет известно, а невязка станет плавно меняющейся функцией. Невязка будет хорошо представляться на более грубой сетке, тогда размерность вспомогательной системы второго уравнения понизится.
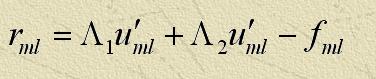
Приблизительно так же будет и в общем случае. Казалось бы, конвейерную обработку можно с успехом заменить обычным параллелизмом, для чего продублировать основное устройство столько раз, сколько ступеней конвейера предполагается выделить. Однако стоимость и сложность получившейся системы будет несопоставима со стоимостью и сложностью конвейерного варианта, а производительность будет почти такой же.
Пример реализации много сеточного метода на трех сетках приведен на анимационном рисунке 1.
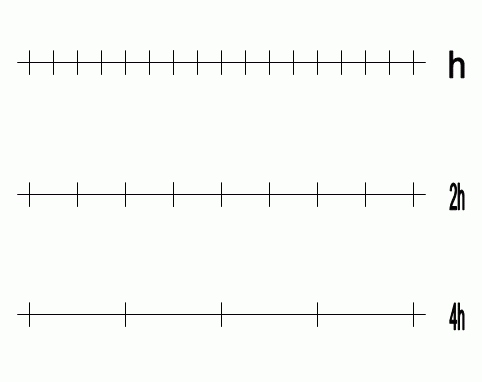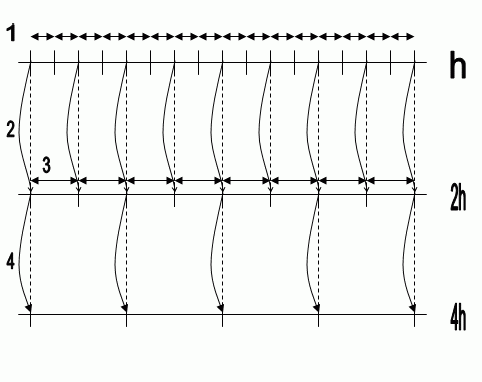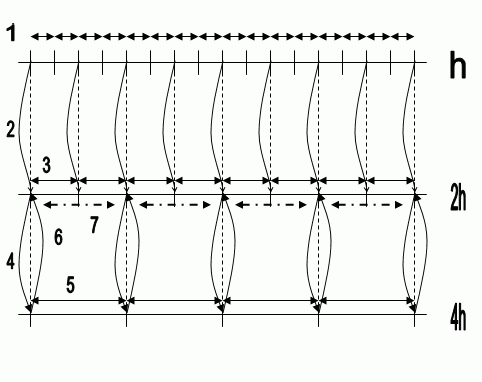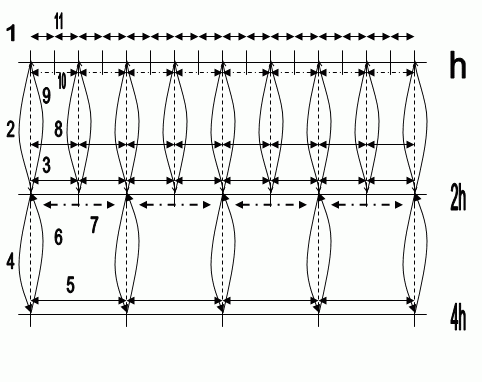
Обозначения приведенного на анимированном рисунке примера:
h – шаг сетки(расстояние между двумя соседними узлами).
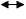- решение полученных уравнений.
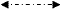- интерполяция полученных значений на более мелкую сетку.
- перенос, полученных при решении, значений на более крупную (мелкую) сетку.
Для реализации многосеточных методов на вычислительном кластере можно использовать несколько типичных топологий связей:
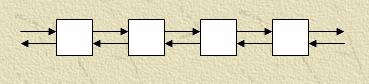
Модификация – Кольцо – соединены между собой концевые процессоры.
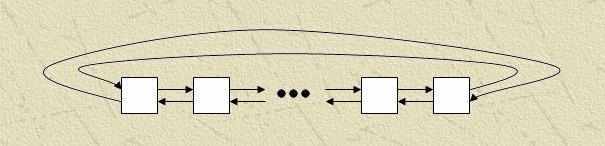
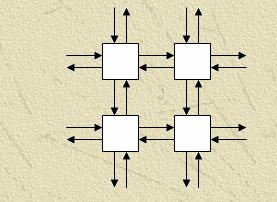
Модификация – Замкнутая решетка – соединены между собой концевые процессоры.
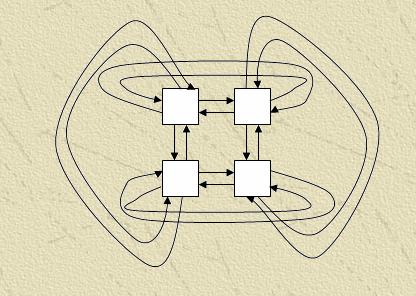
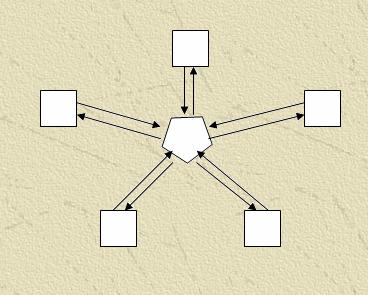
Для удобной реализации программной системы решения многосеточных методов необходимо использовать объектно-ориентированный подход. В данной программной системе основными объектами будут являться сеточные уровни, то есть каждая сетка – отдельный объект. Такое представление делает легким реализацию связей в пределах одной сетки. А переход от грубой сетки к более подробной (или наоборот) будет возможен за счет того, что все объекты являются наследниками одного класса, который содержит полное описание объектов. Система содержит несколько взаимосвязанных подсистем. Подсистемы приведены на рисунке 7.
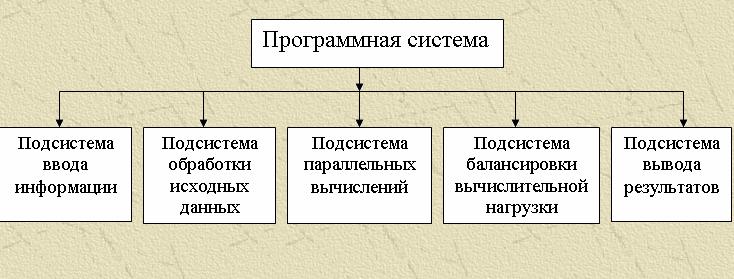
Подсистема ввода информации – предназначена для ввода информации, необходимой для решения.
Необходимо ввести:
Подсистема обработки данных:
Формируются структуры, в которых будут хранится исходные, промежуточные и результирующие данные.
Подсистема параллельных вычислений:
Данная подсистема отвечает непосредственно за реализацию параллельного многосеточного метода для решения дифференциальных уравнений.
Подсистема балансировки вычислительной нагрузки предполагает равномерную нагрузку вычислительных узлов. При появлении новых заданий подсистема балансировки должна принять решение о том, где (на каком вычислительном узле) следует выполнять вычисления, связанные с этим новым заданием. Кроме того, балансировка предполагает перенос части вычислений с наиболее загруженных вычислительных узлов на менее загруженные узлы.
Подсистема вывода результатов – отвечает за удобное для изучения представление полученных результатов.
Необходимо вывести:
Такая структура обеспечивает управление данными, полученными на каждой итерации в процессе решения задачи.
Использование программной системы позволит оценить эффективность и точность параллельного решения задач в частных производных многосеточным методом. В дальнейшем при выполнении магистерской диссертации будет разработана программная система для решения дифференциальных уравнений в частных производных. Реализация параллельного многосеточного метода позволит провести эксперименты расчета уравнений в частных производных, что позволит оценить эффективность и точность производимых вычислений.