Presently one of the most difficult tasks in is the world consider the decision of capacious tasks. It is such tasks, when a necessity is for the decision of thorny calculable problem, for example, decision of the system from 1000 equalizations, conducting of the calculations related to it, comparisons and sorting, neither the clusters of balancing of loading nor clusters of high availability will not help here. For the decision of similar tasks is used the separate type of clusters, which is named calculable or academic.
Calculable clusters (High Performance Computing Cluster) provide the increase of the productivity of having a special purpose applications, if functions of these applications — capacious calculations. Growth of the productivity is straight related to distributing of one calculable process on all accessible sites of cluster.
Research of parallel much-net method of Fedorenko on the calculable cluster of Microsoft Windows Compute Cluster Server 2003 is topically, because such researches were not conducted yet.
The purpose of work is development and realization of the programmatic system, allowing to get the decision of differential equalizations in private derivatives by a much-net method on a calculable cluster.
The main tasks of researches is:
The article of researches are technologies of parallel decision of equalizations in private derivatives on the calculable cluster of Microsoft Windows Compute Cluster Server 2003 with the use of much-net methods.
These researches are executed first in the indicated terms.
The use of the programmatic system will allow to estimate a fast-acting and exactness of decision of differential equalizations a parallel method on a calculable cluster. The programmatic system can be used for the parallel decision of differential equalizations in private derivatives a much-net method.
On results the executed researches an author is do a lecture, at international scientific and technical conference of "Information science and computer technologies" of May, 12-15 2009 taking place in Donetsk in Donetsk National Technical University.
Differential equalizations in private derivatives are the widely applied mathematical vehicle at development of models in the most different areas of science and technique.
One of the most effective way to decision of differential equalizations in private derivatives is much-net approach. Decision is made at first on a rough(large) net, and then carried on more shallow net. It is main feature of this method. Initial decision for the net of NXN, where N – amount of sites, built by means of approximating net (N/2) of x(N/2), got saving of every second site of initial net of NXN. More rough net (N/2) of kh(N/2), in same queue, is approximated the net (N/4) of kh(N/4) et cetera. Then in a private area an error appears as a sum of sinusoid with different frequencies. Then work, executable on a concrete net, diminishes a half frequency component of error, for which diminishing was not attained on more rough nets. Therefore work, producible for decision in every site of net, does a close decision more smooth, that equivalently to suppression high-frequency component of error.
We will consider the close algorithm of decision on net equalization of Puassona:
We will consider net equalization of Puassona on the 5-point template of differential chart "cross":
and, in addition, equalization
where
h – step on co-ordinates,
u – scope terms,
r — discrepancy,
e — error of decision
If the close decision of the first task is known, deciding the second, it will be possible to find the decision of the initial system on a formula 
,
but the decision of task (2) such is exact on complication, as well as decision of initial task.
If you apply an iteration method to the first equalization, doing a few iterations, the close decision of task will be known, and discrepancy will become a fluently changing function. Discrepancy will be well presented on more rough net, then the dimension of the auxiliary system of the second equalization will fall down.
The example of realization of much-net method on three nets is resulted on an animation picture
Denotations of the example resulted on the animated picture:
h – step of net(distance between two nearby sites).
- it is a decision of the got equalizations.
- it is interpolation of the got values on more shallow net.
- it is a transfer, got at a decision, values on more large (shallow) net.
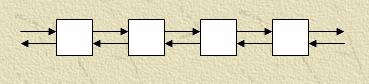
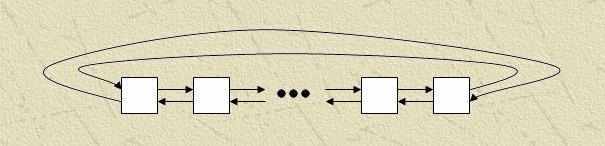
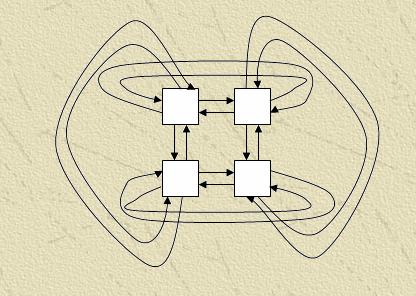
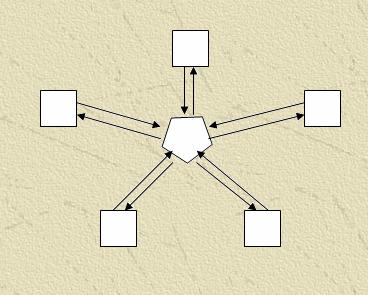
For realization of much-net methods on a calculable cluster it is possible to use a few typical topology connections:
Modification is Ring – end processors are united between itself.
Modification is Reserved grate – end processors are united between itself.
For comfortable realization of the programmatic system of decision of much-net methods it is necessary to use object-aligned approach. The system contains a few associate subsystems. Subsystems are resulted on a picture 7.
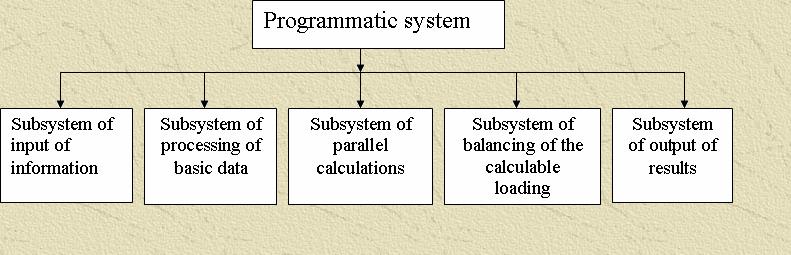
Subsystem of input of information – is intended for the input of information, necessary for a decision.
Subsystem of processing of data:
Structures in which will be kept basic, intermediate and resulting data are formed.
Subsystem of parallel calculations:
This subsystem is responsible directly for realization of parallel much-net method for the decision of differential equalizations.
Balancing of the calculable loading supposes the even loading of calculable sites. Subsystem of output of results –is responsible for comfortable for a study presentation of the got results.
Such structure provides a management data, got on every iteration in the process of decision of task.
The use of the programmatic system will allow to estimate efficiency and exactness of parallel decision of tasks in private derivatives by a much-net method.