Источник: Сборник "PROCEEDING OF THE STUDENTS AND POSTGRADUATES ON COMPUTER SCIENCE AND ENGINEERING", изданного в г. Донецке, в 2007 году, стр. 36-46, Оригинал
Перевод: Солдатов К.А.

Разработка микропрограммных автоматов с преобразователем кодов.

 

Barkalov A.A., Institute of Informatics and Electronics. Zielenogorski University,  POLAND, Lavrik A.S., master degree student, DonNTU, Donetsk, Ukraine

 

Введение

 

Устройство управления (УУ) любой цифровой системы может быть представлено моделью микропрограммного автомата (МПА) Мура или Мили. Аппаратная минимизация УУ, реализованных на Программируемых Логических Устройствах (ПЛУ), может быть достигнута за счет увеличения числа уровней в цепи МПА [1]. В этом случае оптимизация блока микроопераций цифровой системы будет достигаться за счет формирования некоторых дополнительных переменных. [2, 3]. В этой статье предлагается метод, который позволяет уменьшить количество дополнительных переменных, и следовательно, количество ячеек ПЛА для схемы МПА.

 

Главная идея и определения предложенного метода

 

Пусть УУ представлено МПА S с набором состояний , набором логических условий , набором микроопераций  и термов  и пусть каждый терм соответствует одной строке прямой структурной таблице (ПСТ) [1]. Пусть ПСТ имеет Z различных состоянии микроопераций  и пусть состояния  закодированы с помощью использования внутренних переменных , где R = ]log₂M[. Пусть каждый набор Y_z соответствует двоичному коду K(Y_z) с количеством бит равных Q = ]log₂Z[ и пусть они закодированы переменными . Состояния  соответсвует двоичному коду K(a_m) разрядности R. Пусть состояния  и множество  будут объектами МПА S. Основная идея предложенного метода состоит в следующем.

         Первый из объектов (состояние или микрооперация) – это функция терма ПСТ, а второй объект  - это функция одного или может быть нескольких дополнительных элементов. Такой подход основан на включении в структуру МПА специального преобразователя кода (ПК). Если ПК осуществляет соответствие , тогда мы будем называть его как PC_AY – МПА. Если ПК осуществляет соответствие , тогда мы будем называть его PC_YY – МПА. На рисунках 1 и 2 показаны структуры МПА Мура для PC_AY – МПА и PC_YY – МПА. Здесь W представляет собой набор переменных, которые необходимы для точной идентификации объектов [4].

 

Рисунок  1 – Структурная схема автомата Мура PC_AY- FSM

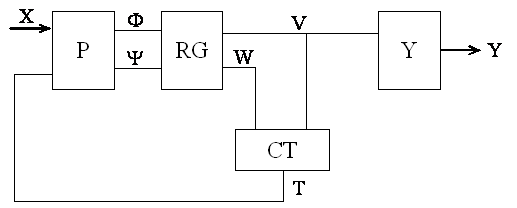
Рисунок  2 – Структурная схема автомата Мура PC_YY-FSM

В виду того, что в автомате Мура выходная функция не зависит от логических условий, подсхема Y реализовывает систему выходных функций Y, которые могут быть подключены к выходным регистрам RG как напрямую (PC_YY – МПА) так и через схему ПК ((PC_AY – МПА). Здесь подсхема P реализует функции возбуждения  и специальную функцию , которая необходима для формирования в RG функции T (PC_AY – МПА) или функции V и W (PC_YY – МПА). PC_AY – МПА не формирует функцию Y, потому что отношение

.                                                       (1)

Истинно, только для конкретного случая МПА Мили. Это является причиной для формирования функции W в МПА Мили PC_AY- МПА (Рис.3) и PC_YY – МПА (Рис.4).

 

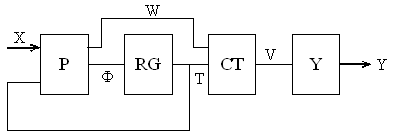
Рисунок  3 –  Структурная схема автомата Мили  PC_AY=МПА

 

Рисунок 4 – Структурная схема автомата Мили  PC_YY-МПА

Если коды объектов, которые формирует подсистема P, то такие объекты называются основными. Если коды объектов являются функциями от других объектов, то они называются вторичными объектами.

 

Общая методика разработки автоматов с преобразованием объектов

 

Методика проектирования любого автомата включает в себя следующие этапы:

1.     Формирование ПСТ МПА. В случае первоначальная информация представляется в виде блок-схемы алгоритма, с отмеченными на ней состояниями.

2.     Определение набора переменных I в точности идентифицирующие вторичные объекты по первичным. Количество переменных во множестве I должно быть минимальным для снижения общего объема требуемых выходов подсхемы P.

3.     Кодирование множества микроопераций  используя элементы множества V. Формирование таблицы микроопераций. Этот шаг выполняется для дальнейшего проектирования ПСТ, количество переменных во множестве V должно быть минимальным, чтобы минимизировать количество выходов подсистемы P.

4.     Кодирование переменных  используя элементы множества , где P = ]log₂K[. Такой подход позволяет свести к минимуму общее количество выходов в подсхеме P и количество входов в преобразователь кода.

5.     Точная идентификация вторичных объектов использую код первичных объектов и код K(I_K) переменных .

6.     Формирование преобразованной ПСТ, в которой исключены столбцы со вторичными объектами и вставлены столбцы с переменными, которые их идентифицируют.

7.     Формирование системы функций, осуществляемых подсхемой P, используя преобразованную ПСТ.

8.     Формирование таблицы преобразователя кодов и его функций.

9.     Разработка логической схемы МПА в заданном базисе.

 

Примеры применения этой процедуры, с подробной информацией для проектирования конкретных структур МПА можно найти в литературе [4,5].

 

Таблица 1- Первоначальная ПСТ МПА Мура

 

Давайте рассмотрим пример МПА Мура, представленного Таблицей 1. Эта таблица содержит Т=4 наборов микроопераций: Y₁=Æ, Y₂={y₁,y₂}, Y₃={y₃}, Y₄={y₃,y₄}, и Q=2 переменных, которых достаточно, чтобы их закодировать: Z={z₁, z₂}. Пусть К(Y₁)=00, K(Y₂)=01, …, K(Y₄)=11. Тогда таблицы микроопераций и преобразователя кодов представлены в таблице 2 и таблице 3 соответственно.

         Функциональная схема МПА показана на рисунке 5. Применение этого метода выгодно, если

R > Q.                                                      (2)

 

Таблица  2 – Таблица микроопераций МПА Мура

 

Таблица  3 – Таблица преобразователя кодов МПА Мура

 

Ссылки на используемую литературу:

 

1.       Baranov S. Logic Synthesis of Control Automata– Kluwer Academic Publishers, 1994. – 312 pp.

2.       Скляров В.А. Синтез автоматов на матричных БИС – Минск: Наука и техника, 1984. – 287 с.

3.       Соловьёв В.В Проектирование цифровых систем на основе программируемых логических интегральных схем. – М.: Горячая линия – Телеком, 2001. – 636 с.

4.       Баркалов А.А., Баркалов А.А. Оптимизация схем автоматов Мура с кодированием наборов микроопераций / В кн. “Автоматизация проектирования дискретных систем”. Материалы 4-й Международной конференции (14-16.11.2001, Минск). Том 2. – Минск: ИТК НАН Беларуси, 2001. – C.14-19.

5.       Баркалов А.А., Палагин А.В. Синтез микропрограммных устройств управления.– Киев: ИК НАН Украины, 1997. – 135 с.

    6. Баркалов А.А. Принцип оптимизации логической схемы микро-программного автомата Мура // Кибернетика и системный анализ. – 1998. - №1. – C. 65-72.

    7. Баркалов А.А., Зеленева И.Я. Оптимизация логической схемы устройства управления с заменой переменных // Управляющие системы и машины. – 2001. - №1.– C.75-78.