INTRODUCTION
Now in the freight market the competition gets new features: against increase of expenses for transportation, toughening of requirements to vehicles, requirements to quality of transportation process have been increased. In such conditions enterprise functioning is impossible without presence of an effective control system. Today the question of transport companies automation ceases to be a question of technologies, now it becomes a tool for increasing business processes efficiency, a way of the new economic activities organization.
One of the most effective variants for solving the problems of cost-saving and improvement of transportation process quality is introduction of information routing, account and planning systems at the transportation enterprise. In particular, such real tool of development is the system of truck haulages’ optimization.
1 THEME’S ACTUALITY
Creation of optimized routes allows to define exact volume of truck haulages from the purchasing and trading enterprises, quantity of the vehicles which carry out these transportations. Also it promotes reduction of the idle time of cars for loading and unloading, effective use of fleet of vehicles and liberation of considerable consumer’s material resources from spheres of circulation. Thus, development of optimum routes and projects of transportation plans will promote timed and uninterrupted performance of product deliveries and effective interaction of the organizations-suppliers, the organizations-receivers and the transportation organizations.
Summing up the aforesaid can tell with the confidence, that the problem of truck haulage's optimization becomes especially actual in the conditions of the given economic situation.
2 COMMUNICATION OF WORK WITH SCIENTIFIC PROGRAMS, PLANS, THEMES
Qualification master’s work was carried out during 2008-2009 years according to scientific directions of the chair «Automated control systems» of Donetsk National Technical University.
3 PURPOSE AND RESEARCH TASKS
As there is a considerable quantity of delivery objects it is necessary to optimize routes of transportations and operatively to react to all changes. Hence, it is possible to define the work purpose: To develop algorithm of truck haulages' optimization taking into account time windows and capacity of vehicles. For achievement this purpose it is necessary to solve following basic problems:
- to formulate mathematical statement of the routing transport problem taking into account the restrictions;
- to choose (develop) optimization criteria;
- taking into account a solved problem to develop a way of solution coding, problem-oriented crossover and mutation operators;
- to develop the modified genetic algorithm of truck haulages' optimization taking into account time windows and capacity of vehicles;
- experimentally to check up an algorithm overall performance.
Object of researches are routes for truck haulages of transport enterprise.
Subject of researches are methods and algorithms for solving the vehicle routing problem.
Methods of researches. We use in work system analysis methods, the Clarke-Wright method, heuristic insertion methods and genetic algorithms.
4 THE SCIENTIFIC NOVELTY
The scientific novelty of the work consists in development of the new approach to solving vehicle routing optimization problem. The idea of the given approach consists in shared use of the Clarke-Wright method, heuristic methods and the modified genetic algorithm. The Clarke-Wright method and insertion heuristic methods are used to find effective initial solutions, forming thus the initial population. And the modified genetic algorithm allows to improve initial solutions, approaching them to the optimal.
5 PRACTICAL IMPORTANCE OF THE RECEIVED RESULTS
In the conditions of transport enterprise the offered subsystem allows to solve such problems, as development of the optimal plan of truck haulages, accumulation and representation fact data about transport use in a convenient for the analysis form. The analysis of the stored in system information allows to provide optimal planning of new cars acquisition and an effective uses of the rented transport. By means of such systems the dispatcher can quickly calculate optimal routes on the basis of the demands for delivery, the list of own and rented vehicles, clients and depot addresses. Thus calculated routes will be optimized by such criteria, as the minimum cars mileage and the maximum loading of each car.
6 REVIEW OF RESEARCH AND DELELOPMENT
At the present time many leading firms, organizations work in the sphere of transport logistics, trying to improve existing systems. Scientists and experts all over the world are engaged in search of new methods and improvement of old algorithms which will allow to receive even more productivity of algorithms and they are able to find new best suboptimal solutions for a vehicle routing problem. Unfortunately, in Ukraine the given theme doesn’t have sufficient reflection in scientific publications, and research of methods for solving the problem has not received due development. At local level (within DonNTU) the vehicle routing problem has not been presented in scientific works.
Let's consider existing methods and tools applied to solve the given problem at global level.
6.1 Review of existing methods
6.1.1 Clarke-Wright method
Clarke-Wright method has been developed by two British scientists G. Clarke and J.W. Right [1]. Despite prescription of development, till now it remains one of the most popular methods for the solution of the given problem, on what practice of its application testifies. The Clarke-Wright method belongs to approximate, iterative methods and is intended for the computer solving of a transport problem. This algorithm uses the concept of savings to rank merging operations between routes. The savings is a measure of the cost reduction obtained by combining two small routes into one larger route. Advantages of the method are its simplicity, reliability and flexibility. The average error of the decision does not exceed 5-10 %[2]. However, considering greedy character of Clarke-Wright algorithm, the received solutions have often insufficient quality relative to ones received by more difficult approaches.
6.1.2 Heuristic insertion methods
The best solution for concrete initial data can be found by sequential application of various heuristic methods, using total distance of the received route as a comparison estimation of solution quality [3]. We will consider 4 most popular heuristic algorithms:
- The nearest neighbor [4];
- The nearest town [4];
- The most cheap inclusion [4];
- The minimum spanning tree [4].
In the nearest neighbor method, points of the plan consistently are inserted in a route, and, each next included point should be the nearest to the last chosen point among all the others which have not been included in structure of a route yet.
The Nearest town method on each step of the algorithm builds a feasible route on a current subset of points already included in a route, adding to it new point from those, that have not been included in a route yet for which there will be the nearest neighbour among points, that already belong to a route.
The Most cheap inclusion method on each step of algorithm builds a feasible route basing on a current subset of points, which have already been included in a route, adding to it the new point which inclusion between some adjacent points leads to the minimum increase of route’s cost (distance).
However any heuristic method is based on formally not educated guesses, therefore it is impossible to prove, that the heuristic algorithm for any initial data finds suboptimal solutions.
6.1.3 Tabu search
The founder of meta-heuristic tabu-search algorithm is F.Glover. He offered an essentially new scheme of local search [5]. Tabu search is a meta-heuristic algorithm that guides a local search to prevent it from being trapped in premature local optimum by prohibiting those moves that cause returning to previous solutions and looping [6]. The basic mechanism that allows the algorithm to avoid a local optimum is tabu list, which is updated at the end of each iteration. The choice of the best solution in the neighbourhood is done such that it does not adopt any of the tabu attributes. The tabu search is perspective algorithm; however introduction of penalties for restrictions violation in criterion function doesn’t give guarantees of finding feasible solutions.
6.1.4 Branch and bound method, branch and cut method
The branch and bound method is a well-known variant of search with returning and is the only special type of search with restrictions [3,6,7]. The restrictions are based on the assumption, that each solution is connected with certain cost and that it is necessary to find the optimum solution (the solution with the least cost). For application of this method cost should be accurately defined for partial solutions. We can reject the partial solution if its cost is more or equal to cost of the previously calculated solutions [8]. This check eliminates viewing of some parts of a tree, but actually it is weak enough and allowed deep penetration in a tree before branches break. Therefore the branch and bound method and the branch and cut method are not effective on performance time.
As the given methods belong to the class of exact methods, it’s impossible to apply them to our problem of big dimension.
6.1.5 Ant colonies algorithms
Ant colonies algorithms represent probabilistic greedy heuristics, where probabilities are established proceeding from the information of the solution quality, that have received from the previous solutions [9]. Idea of the ant algorithm is simulation of ant’s behaviour, which connected with their ability to find quickly the shortest way from an ant hill to a source of food and to adapt for changing conditions, finding a new shortest way. In the movement an ant marks a way by pheromone, and this information is used by other ants for a way choice. This elementary behaviour rule defines ability of ants to find a new way if old would be appeared unavailable. Good results in many respects depend on initial tuning of the parameters. The given algorithm is effective only with use of additional methods, such as local search [10].
6.1.6 Genetic algorithms
The algorithm for solving optimisation problems, based on ideas of a heredity in biological populations, for the first time has been offered by John Holland (1975) [9,11]. In GA each individual represents the potential solution of some problem. Each individual is coded by chromosome, which is a string of gene. A population is a set of individuals, each of them is a potential solution. Search of the (sub)optimum solution of a problem is carried out in the population evolution process. During this process one terminate set of solutions is transformed to another by means of genetic operators, such as a reproduction, crossover and mutation. Presence of whole solution "population" at genetic algorithms together with the probabilistic mechanism of a mutation, allows to assume smaller probability of a finding local optimum and bigger overall performance on a multiple-extreme landscape. Results genetic algorithms application are presented in articles [12,13].
6.2 Review of the existing tools
6.2.1 ArcLogistics 9.3
The given software product is developed by known American firm ESRI. The corporation ESRI (USA) – is one of the world leaders in development, creation and promotion of geoinformation systems. Today ESRI has 2 700 employee in the USA, 1 900 of which are based at its corporate staff in California. The heads are assured, that the technology of geographical information system should develop constantly to meet changing requirements of business, industry, the governments and education.
ArcLogistics 9.3 is a tool for planning and optimization of fleet’s work. Main advantages of ArcLogistics 9.3 are distribution of orders on park of vehicles, presence of road data on all territory of Europe, compatibility with other ESRI software products, the account of time windows, a considerable quantity of vehicles’ characteristics, tools of communication with external systems through ODBC, work with pair orders, various reports. Cost of the given product is $12500.
6.2.2 TruckStops
TruckStops – is the software product developed by firm MicroAnalytics. TruckStops – is the leading software for vehicle routing and planning. It is designed for the companies using 5 or more vehicles. You can receive profit in: full time of trips, kilometers, payment to drivers, service of the vehicles and fuel cost. TruckStops uses allows firms to reduce delivery cost, improves service given to the client, makes effective routes, increases administration managerial control. Program cost is $1650.
6.2.3 Business card
Business card – is the software product developed by firm INGIT. It possesses the powerful and flexible mechanism of cargo delivery calculation. At the expense of the flexibility this mechanism can be applied practically to any specific problem, such as cargo delivery from the central depot, delivery of cargoes from different places on the central depot, cargo delivery from several warehouses, delivery on some depots, and also to the problems, that don’t have the central points etc. However, flexibility has also the underside. It’s necessity for the considerable quantity of entrance data. The main feature of the given program is embedding in 1C system. Program cost is $1200.
However software products of all these firms have one common fault - is the big cost. Their purchase involves a huge overpayment for unnecessary functionality of a system. Besides, the order and installation of these foreign products will cause additional transport expenses, and their price considerably will increase. Keeping the copyright, any bought software product is delivered without initial codes of program modules, and each additional tuning or change of any working conditions are connected with additional payment. Also we have no possibility to receive the authentic and full information on the method used in the program, and it does not allow us to estimate an optimality of the found solution and efficiency of the given software product use. Business card has one more lack. It is developed for integration in 1C system, but it’s the undesirable factor for our enterprise.
7 MATHEMATICAL STATEMENT OF THE VEHICLE ROUTING PROBLEM
The Vehicle Routing Problem (VRP) is a NP-hard combinatory optimisation problem. The given problem with Time Windows and restriction on capacity can be described as follows [14].
There is the one central depot O, which uses a quantity of independent vehicles with identical delivery capacity Q to serve demands di from N customers,  . It is required for each vehicle to make a route it can serve a number of clients on. Each client has to be served by one car only. There is a matrix, that consists of distances between clients and the depot and calculated cost price of one travelled kilometre taking into account fuel consumption, maintenance operation of cars, drivers’ salaries, etc. Basing on these data the costs of the distances between clients and the depot are calculated (figure 7.1). . It is required for each vehicle to make a route it can serve a number of clients on. Each client has to be served by one car only. There is a matrix, that consists of distances between clients and the depot and calculated cost price of one travelled kilometre taking into account fuel consumption, maintenance operation of cars, drivers’ salaries, etc. Basing on these data the costs of the distances between clients and the depot are calculated (figure 7.1).

Figure 7.1 – The matrix of distance’s costs
The vehicles must accomplish a delivery with a minimum total length cost S. The distance between the customers is symmetric, i.e.,  , where , where  is the distance’s cost from client i to client j, where is the distance’s cost from client i to client j, where  . A solution for the VRP would be a partition . A solution for the VRP would be a partition  of the N demands into K routes, К --> min. Each route begins and ends at the depot. Then the Vehicle Routing Problem of optimisation can be formulated as a minimisation of the total length cost taking into account the following restrictions: of the N demands into K routes, К --> min. Each route begins and ends at the depot. Then the Vehicle Routing Problem of optimisation can be formulated as a minimisation of the total length cost taking into account the following restrictions:
 |
(7.1) |
 |
(7.2) |
 |
(7.3) |
 |
(7.4) |
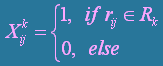 |
(7.5) |
where – subroute from the client i to the client j, upper index k marks the corresponding route, where – subroute from the client i to the client j, upper index k marks the corresponding route, where  , K – is a quantity of routes. , K – is a quantity of routes.
The second restriction means, that each client is served only by one vehicle and only once. The third restriction defines, that the vehicle cannot serve more clients, than its capacity allows. di,  , – is a demand of the corresponding client, N – is a quantity of clients. The fourth restriction is a time restriction; car’s arrival to the client should not be later than a target date. , – is a demand of the corresponding client, N – is a quantity of clients. The fourth restriction is a time restriction; car’s arrival to the client should not be later than a target date.  – is an arrival time of corresponding k-th car to the client i, – is an arrival time of corresponding k-th car to the client i, – is the latest time to visit customer i. – is the latest time to visit customer i.
8 THE COMBINED APPROACH FOR ROUTES’ OPTIMIZATION
As an algorithm of the truck haulage's optimisation problem it was offered to use the new genetic algorithm improved by heuristic methods with the modified problem-oriented operators. The general structure of the algorithm offered is presented in figure 8.1.
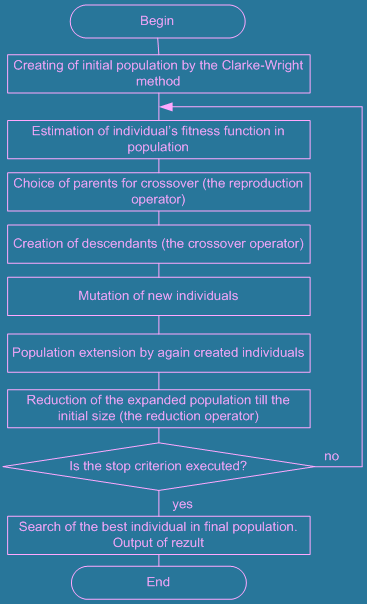
Figure 8.1 – The integrated algorithm of the advanced genetic approach
Taking into account a character of the problem genetic material of the individual has to contain some routes that are made of the sorted subset of the clients. For example, the chromosome from the figure 8.2 represents the solution presented in the figure 8.3.

Figure 8.2 - The example of solution coding into a chromosome
Figure 8.3 – The example of VRP solution
(animation: volume - 8000 byte; size - 450х315; consists of 113 frames; a delay between frames - 80 msec; a delay between last and the first frames - 0 msec; quantity of recycle - 0)
Let's consider in detail algorithm’s blocks. Initial population is formed by the Clarke-Wright heuristic method, heuristic insertion methods and the arc interchange method, named  interchange. It allows us to receive a good initial population for an evolutionary search and to reduce an operating time of the genetic algorithm. For an estimation of the received solution’s (chromosome’s) quality we use the following fitness function: interchange. It allows us to receive a good initial population for an evolutionary search and to reduce an operating time of the genetic algorithm. For an estimation of the received solution’s (chromosome’s) quality we use the following fitness function:
 |
(8.1) |
where  – is a penalty connected with the time restriction violation for i-th client. If delivery is planned in time the penalty is zero, otherwise it grows with a delay increase of a holding time. The idea of a taboo-search for estimation of solutions is applying of penalties for restriction violation. And it lays at the basis of the given fitness function. – is a penalty connected with the time restriction violation for i-th client. If delivery is planned in time the penalty is zero, otherwise it grows with a delay increase of a holding time. The idea of a taboo-search for estimation of solutions is applying of penalties for restriction violation. And it lays at the basis of the given fitness function.
The selection operator is based on the ranging method, in which a probability of selection for each individual depends only on its position (number) in a set of individuals, which is ordered on value of the criterion function, instead of the value of fitness function. In comparison with the roulette method the given approach increases probability of individual choice with small values of the criterion function. It promotes population development in all directions.
The modified crossover operator, which considers specificity of the given problem, was offered for offspring’s creation . The quantity of the parents that take part in crossing is defined by the number M. Increase of M allows to transfer properties (routes) of parents to offspring more effectively, thus convergence of algorithm are being increased, but it threatens being trapped in local minimum. With a reduction of M a diversity grows in population. Optimal value of parameter M varies between 2 and 4. The crossover operator consists in the following:
- Routes of the chosen individuals are integrated in one solution, named an incorporated solution;
- As long as there are routes in the incorporated solution, the following is being done: choose a route and insert it into the new solution. For this purpose take a random number between 0 and quantity of routes in the incorporated solution. The given number specifies the route number in the incorporated solution. Then delete from the incorporated solution the chosen route and all the routes, in which there are clients from the chosen solution;
- Insert the clients that haven’t been served yet into the new solution with use of the most cheap inclusion method taking into account capacity. If the insertion is not possible, then the new route is created.
On the basis of the modern research analysis of leading scientists in the sphere of a question on optimal vehicle routing and features of the given problem a number of mutation operators was developed. This operators are applied with corresponding probabilities , which must not violate the following restriction: , which must not violate the following restriction:
 |
(8.2) |
Size  in the given formula represents a general probability of a mutation in a chromosome, and it equals to 7 %. in the given formula represents a general probability of a mutation in a chromosome, and it equals to 7 %.
Mutation operators:
- swap: select two clients and swap them. Selected points can belong to the same or to different routes. If created solution is infeasible, then the correction operator is applied;
- inversion: select a sub-route and reverse the visiting order of the customers that belong to it. If it has got worse value of fitness function for the given solution, then the given operator is cancelled;
- displacement: select a sub-route and insert it in another place. This operator can perform intra or inter displacement;
- secondary insert of routes: routes are deleted entirely from the solution, and then the clients from remote routes are inserted into the solution anew;
- secondary insert of clients: single clients are deleted from the solution, and then they are inserted into a route anew;
- restoration: delete the clients, which violate the time restriction from their routes. Then remote clients are inserted repeatedly, using the most cheap inclusion method taking into account vehicle’s capacity;
- reordering of clients: it’s a procedure of an intensification, that tries to reduce full distance of feasible solutions, reordering clients within a route by means of the heuristic insertion method.
The correction operator is directed towards correction of restriction violation for infeasible solutions. It deletes the clients that violate restriction from routes, and tries to reinsert them in another route to generate a feasible solution. In case if it is impossible – the new route is created.
The reduction operator selects 5 % of elite chromosomes into new population, then missing quantity of individuals is formed by the roulette method.
As a stop criterion we use either quantity of generations or absence of average value improvement of fitness function during several iterations.
CONCLUSION
As a result of a research work materials on the questions connected with a theme of master’s diploma have been collected and studied. Applied methods and algorithms of routes’ optimization and developments of the leading firms, offered tools and software have been investigated. Advantages and disadvantages of the existing computer systems and the methods of optimization have been revealed. As result problems, unresolved in these directions, possible ways and methods of their improvement have been defined. Basing on these results of the analysis the direction of our researches towards finding of optimal routes for realization of the truck haulages has been chosen, mathematical statement of the problem is formulated. The combined genetic algorithm has been developed for solving the offered problem. It based on the evolutionary approach with use of the Clarke-Wright method for creating of initial population. The heuristic insertion methods are used as the mechanism of population‘s development and for correction of the solutions that violate the restrictions. The offered algorithm has been implemented in the high level language in the environment C++ Builder 6.0. A result of the program is the set of optimized routes which are represented as itinerary lists with indication on necessary data of orders and clients. The further work consists in planning and carrying out of experimental researches and in estimating of optimization algorithm’s efficiency.
LIST OF USED LITERATURE
1. Clarke G. Scheduling of vehicles from a central depot to a number of delivery points / G. Clarke, J.W. Wright // Journal of Operations Research Society. - 1964. – Vol.12, № 4. – pp. 568–581.
2. Battarra M. Tuning a Parametric Clarke-Wright Heuristic via a Genetic Algorithm / M. Battarra, B. Golden, D. Vigo // Journal of Operations Research Society. - 2008. – Vol.59, № 11. – pp. 1568–1572. / - Режим доступа к статье:
http://or.ingce.unibo.it/ricerca/technical-reports-or-ingce/papers/gacw-sito.pdf.
3. Рейнгольд Э. Комбинаторные алгоритмы. Теория и практика. / Э.Рейнгольд,
Ю. Нивергельт, Н. Део; пер. с англ. Е.П. Липатова. - М.: Мир, 1980. — 476 c.
4. Пушкарёва Г.В. Исследование и применение бионических методов и моделей
для автоматизированного проектирования маршрутов обхода геометрических объектов [Электронный ресурс] // Компьютерная графика и представление GraphiCon ‘2005: науч.-техн. конф., 20-24 июня 2005г. : - 2005. / - Режим доступа к статье:
http://www.graphicon.ru/2005/proceedings/papers/Pushkaryova.pdf.
5. Glover F. Tabu Search/ F. Glover, M. Laguna // Journal of the Operational Research Society. - 1999. – Vol.50, № 1. – pp. 106–107. / - Режим доступа к статье: http://glossary.computing.society.informs.org/notes/spanningtree.pdf.
6. Сухарев А.Г. Курс методов оптимизации: Учебное пособие. - [2-е изд]. / А.Г. Сухарев, А.В. Тимохов, В.В. Федоров. – М.: ФИЗМАТЛИТ, 2005. – 368 с.
7. Blasum U. Application of the Branch and cut method to the Vehicle Routing Problem [Электронный ресурс] / U. Blasum, W. Hochstattler. - 2000. / - Режим доступа к статье:
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.9.9887&rep=rep1&type=pdf.
8. Харчистов Б.Ф. Методы оптимизации: учебное пособие / Б.Ф. Харчистов. – Таганрог.: ТРТУ, 2004. – 140 с.
9. Макконелл Дж. Основы современных алгоритмов: учебное пособие / Дж. Макконелл; пер. с англ. С.К. Ландо. – [3-е изд.]. - М.: Техносфера, 2004. — 368 c.
10. Штовба С.Д. Муравьиные алгоритмы / С.Д. Штовба // Exponenta Pro. Математика в приложениях. - 2003. – № 4. – С. 70-75 / - Режим доступа к статье: http://soft.mail.ru/journal/pdfversions/32150.pdf.
11. Рутковская Д. Нейронные сети, генетические алгоритмы и нечеткие системы / Д. Рутковская, М. Пилиньский, Л. Рутковский; пер. с польск. И.Д. Рудинский – М.: Горячая линия-Телеком, 2006. – 452 с.
12. Pereira F.B. GVR: Vehicle Routing Problem: Doing it the Evolutionary Way / F.B. Pereira, J. Tavares, P. Machado, E.Costa // Proceedings of the Genetic and Evolutionary Computation Conference – 2002. – p. 690. / - Режим доступа к статье: http://osiris.tuwien.ac.at/~wgarn/VehicleRouting/GECCO02_VRPCoEvo.pdf.
13. Pereira F.B. GVR: a New Genetic Representation for the Vehicle Routing Problem / F.B. Pereira, J. Tavares, P. Machado, E.Costa // Proceedings of the 13th Irish Intern. Conf. on Artificial Intelligence and Cognitive Science – 2002. – pp. 95-102.]
/ - Режим доступа к статье: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.61.5248.
14. Смехов А.А. Основы транспортной логистики. / А.А. Смехов. - М.: Транспорт, 1995. - 197 с.
15. Архангельский А.Я. Программирование в C++Builder 6 / А.Я. Архангельский. – М.: БИНОМ, 2003. – 1152 с.
TOP |


 of the N demands into K routes, К --> min. Each route begins and ends at the depot. Then the Vehicle Routing Problem of optimisation can be formulated as a minimisation of the total length cost taking into account the following restrictions:
of the N demands into K routes, К --> min. Each route begins and ends at the depot. Then the Vehicle Routing Problem of optimisation can be formulated as a minimisation of the total length cost taking into account the following restrictions: 



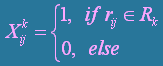
 , K – is a quantity of routes.
, K – is a quantity of routes.  , – is a demand of the corresponding client, N – is a quantity of clients. The fourth restriction is a time restriction; car’s arrival to the client should not be later than a target date.
, – is a demand of the corresponding client, N – is a quantity of clients. The fourth restriction is a time restriction; car’s arrival to the client should not be later than a target date. 


 – is a penalty connected with the time restriction violation for i-th client. If delivery is planned in time the penalty is zero, otherwise it grows with a delay increase of a holding time. The idea of a taboo-search for estimation of solutions is applying of penalties for restriction violation. And it lays at the basis of the given fitness function.
– is a penalty connected with the time restriction violation for i-th client. If delivery is planned in time the penalty is zero, otherwise it grows with a delay increase of a holding time. The idea of a taboo-search for estimation of solutions is applying of penalties for restriction violation. And it lays at the basis of the given fitness function.