This paper presents an application of independent component analysis to electrogastrogram (EGG), which is a gastric myoelectrical activity measured by several electrodes attached on the abdomen. The purpose is to remove the interfering signals other than the gastric activity.

Our analysis is done under the assumption that electrical activities of the organs near the electrodes are statistically mutually independent of each other and the EGG data is a convolutive mixture of them. The result shows that the proposed method is able to clearly extract the component originated from the the gastric activity.

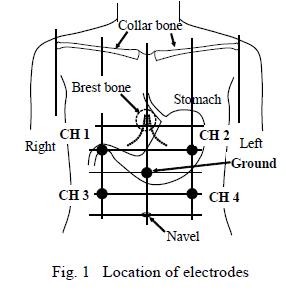
Eelectrocgastrogram (EGG) is the recording of gastric myoelectrical activity by several electrodes attached on the abdomen. A configuration of the electrodes is shown in Fig.1. A crucial problem in analyzing EGG data is that the signals detected by the electrodes do not only contain the signal of interest, namely the component originated from the stomach, but also those from other organs near the stomach. In order to use EGG data for clinical purpose, it is required to remove the interfering signals other than gastric activity itself. In healthy humans the frequency range of the stomach-originated signals is localized around 3 [cycles / min] (5×10⁻² [Hz]).

A method for extracting the gastric component might be to apply a band-pass filter to EGG data. It is however difficult to do so because the frequency range of gastric signal overlaps with that of the signals originated from other organs and moreover the frequency characteristics of those signals are rarely known.

In such a situation the technique of independent component analysis (ICA) seems to be effective, in which no information about the frequency characteristics of the sources is required. ICA is a statistical technique to extract the set of independent components only from given data. We assume that the signals produced by different organs are statistically independent and EGG data is an observation of their mixture though, strictly speaking, it might not be true.

In general a mixing process is classified into either of two types: instantaneous mixture and convolutive mixture. In [7] and [12], the mixing process in EEG is assumed to be instantaneous. In our approach, oppositely, we treat the mixing process as a convolutive one because the gastric myoelectrical wave is governed by gastric peristalsis and hence the signal from the stomach is measured by the electrodes with different delays.
In conventional algorithms for convolutive mixture of sources, each source signal is usually assumed to be independent and identically distributed (iid).[8] However, such approaches are not suitable for EGG data because the component produced by the stomach may have a strong periodicity. The reason of why the assumption of iid is unsuitable for convolutive mixture of periodic source signals is described in [9]. In this paper we use a new algorithm without the assumption that sources are iid. The algorithm was derived by one of the authors, based on two principles called “minimal distortion principle” and “inverse minimal distortion principle.” [11]

This paper is organized as follows. In section II we describe some mathematical notations used in this paper. Section III provides a formulation of ICA for the readers unfamiliar with its concept. Section IV, V and VI show the details of derivation of our algorithm used in the analysis of EGG. Section VII shows a result of the application of the algorithm to EGG. Section IIV is devoted to the conclusion.

II. Mathematical notations

In this section we describe mathematical denotations for matrices appearing in the following sections. Below, matrix X and transfer function matrix X(z) = Σ_τX_τ z^−τ are M×N matrices. X can be complex-valued while coefficients X^τ of X(z) are real-valued.

Frequency transfer function X(e^j2πf) associated with X(z) is denoted by X(f) . If a square matrix X(f) is nonsingular for every frequency f, X(z) is said to be nonsingular. If M ≥ N (M ≤N) and X(z)X^H(z) (X^H(z)X(z)) is nonsingular, then X(z) is said to be full column (row) rank. Furthermore if X(z) is full column (row) rank, its pseudoinverse X^†(z) is defined as (X^H(z)X(z))⁻¹X^H(z) (X^H(z)(X(z)X^H(z))⁻¹).

tr X represents the trace of square matrix X. The Frobenius norm of matrix X is defined as ||X||=(trXX^H)^1/2. Also the Frobenius norm of transfer function X(z) is defined as ||X(z)|| = (Σ_τ||X_τ||²)^1/2.or equivalently || X(z) || = (∫^{1/ 2} _{-1/ 2} ||X ( f ) || ²df )^1/2.
diag {d1, ..., dN} represents the diagonal matrix with diagonal entries d1, ..., dN. Given a square matrix X, diag X (off-diag X) sets its off-diagonal (diagonal) entries to zeros.