Tsukanov Andrey

Faculty: "Computer Information Technologies and Automatics"

Department: Automatics and telecommunications

Speciality: The telecommunication systems and networks

Theme of master's work: «Development and research of methods of variable rate sampling of signals in telecommunication systems»

Leader of work: Degtyarenko Ilya

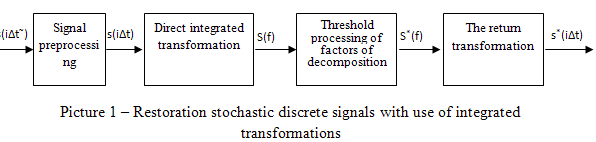
Abstract

One of basic telecommunication system tendency is its digitization. In any digital system one of the most important parameter is sampling. Quality of system work depends from accuracy of this parameter. Undesirable phase and/or frequency random discrecity period departures are calling jitter. It may arise in the issue of master oscillator instability, line parameter changing in time and different frequency component propagation speed of same signals [1]. Jitter is one of main problems digital electronics device development, specifically digital interfaces. Not enough careful jitter calculation can lead to its accumulation while signal forwarding in digital channel and, at the end, to device nonoperability.

In telecommunication sphere jitter and its consequences prevention passes by the instrumentality of buffer storage, PLL devices, special linear code use, and clock synchronization dedicated line creation. Basically this solution presupposes hardware support. But in certain cases postprocessing and signal extraction by software tools can take place. This work is about jitter minimization devices progress on discretization signal phase. Per se, jitter deletion task adds up to restoration of stochastically sampled signal characteristics. [2]

One of the new, not enough explored now, restoration of stochastically sampled signal characteristics approach is method which uses integral transformations [3]. This method conception can be shown as a scheme (pic. 1).

According to this structure irregularly sampled signal s(iΔt~) conversion to signal with fixed lead s(iΔt) takes place on the fist step. Then direct integral transform takes place, which convert signal from time representation to frequency. The alias components have broadband noise-type spectrum in stochastic sampling [5], and according to this they can be minimized by expansion coefficient thresholding S (f). After this inversion is performed, i.e. a signal s*(iΔt) is generated that has constant sampling step with reduced alias component levels. Fourier discrete transformations (DFT) may be used as integral transforms in this structure or its version – discrete cosines transformation (DCT) and discrete sinus transformation (DST) [4].

But this structure isn’t unique because it can be used only for stationary signals restoration that have line spectrum, as Fourier transformations make signal characteristics averaging-out on whole cultivated signal part, as follows local features may be lost.

Using of wavelet signal decomposition as integral transform may help to avoid this problem. It doesn’t have such defects [4]. This expansion is given by [8]

    (1)

where ψ(t) – parent function (parent wavelet);

а – the factor setting plotting scale of wavelet (it is found to frequency);

            b – the factor setting position of wavelet (it is proportional to time).

On practice discrete wavelet signal transformation is used more often, as it may be realized using LF and HF filters set detailed expansion coefficients arrive as a result of pass though LF-Filter, and approximations coefficients are a result of HF filtering .

Advantages of this signal decomposition method are:

·         Features of all local signals, which stores all transferred information, are taked into account.

·         This expansion is simple in realization and doesn’t make additional superfluity in initial data.

·         Back transformation also is realized by using filters.[9]

In this work a new way of jitter that occurred on sampling phase prevention was offered. This method is based on using of пороговой treatment of wavelet signal decomposition. It also may be used for lost digital signal sample reconstruction. This method using in telecommunication systems can help to increase information transferring reliability.

References:

1. Джулиан Данн. Джиттер. Теория. Audio Precision. http://www.ixbt.com/proaudio/jitter-theory-part3.shtml

2. Сторожук Н.Л., Белоруков  В.А., Щитников  В.И., Еще раз о джиттере. Метрология и измерительная техника в связи 2 2006г. 49-52с.

3. Дегтяренко И.В., Афанасьев Д.Н. Алгоритм восстановления стохастически дискретизированых сигналов, Наукові праці ДонНТУ. Серія «Обчислювальна техніка та автоматизація. Випуск 15.- Донецьк: ДонНТУ, 2008- 36-41с.

4. Bilinskis I. Digital alias-free signal processing. – Willie, 2007. – 430 р.. 

5. Дмитриев В.И. Прикладная теория информации: Учебник для вузов.- М.: ВШ, 1989г.320 с.   

6. Beutler F.  Alias – free randomly timed sampling of stochastic processes. — IEEE Trans. Inf. Theory, Vol. IT- 16, No. 2, 1970. pp. 147–152 с.

7. Корн Г., Корн Е. Справочник по математике для научных работников и инженеров. – М.: Наука, 1973г, 831с.

8. Дьяконов В.П. Вейвлеты. От теории к практике. – М.: СОЛОН-Р, - 2002. – 448 с.

9. Астафьева Н.М. Вейвлет-анализ: Основы теории и примеры применения. – Успехи физических наук, 1996, т.166, № 11,  1145-1170с.

10. Левкович-Маслюк Л, Переберин А. Введение в вейвлет-анализ: Учебный курс. – Москва, ГрафиКон’99, 1999. 120c.