АЛГОРИТМ ВОССТАНОВЛЕНИЯ СТОХАСТИЧЕСКИ ДИСКРЕТИЗИРОВАННЫХ СИГНАЛОВ

Доц. Дегтяренко И.В., Афанасьев Д.Н.

Источник: Наукові праці ДонНТУ. Серія «Обчислювальна техніка та автоматизація. Випуск 15.- Донецьк: ДонНТУ, 2008- с.36-41.

            Общая постановка проблемы.

На сегодняшний день методы равномерной дискретизации сигналов по времени являются доминирующими, вследствие хорошо разработанных теоретических основ и относительной простоты практической реализации. Однако при решении целого ряда задач данные методы являются мало эффективными и уступают по некоторым показателям методам неравномерной дискретизации [1,2]. В частности, методы неравномерной дискретизации позволяют во многих случаях более компактно представлять информацию, содержащуюся в сигнале, а так же повысить помехоустойчивость измерительных преобразователей.

Одним из наиболее перспективных методов данного класса является метод стохастической дискретизации [1,3], при котором шаг дискретизации является случайной величиной с известным законом распределения. Необходимость использования теории стохастической дискретизации в ряде случаев обусловлено наличием вариации задержки (джиттера) при дискретизации реальных сигналов. Джиттер может быть вызван невозможностью обеспечения бесконфликтного опроса с равномерным шагом (для многоканальных систем), либо когда сама аппаратура измерительного канала не может обеспечить строго равномерный шаг дискретизации, например, ввиду асинхронности работы некоторых блоков. Кроме того, использование данного метода дискретизации позволяет упростить требования к входным измерительным цепям из-за отсутствия необходимости антиалиасной фильтрации [1,3]. Дело в том, что при стохастической дискретизации алиасные компоненты сигнала превращаются в широкополосный шум, в отличие от варианта равномерной дискретизации, когда данные компоненты имеют детерминированную структуру.

Задача восстановления сигналов по неравномерной выборке отсчетов традиционно решается с привлечением теории интерполяции. Классическим является подход, основанный на построении интерполирующей функции во временной области. В качестве интерполирующих функций чаще всего используются линейная и квадратичная интерполяции, ряды Тейлора, полиномы Лагранжа, сплайны [4,5].

Приближение функций рядом Тейлора имеет много недостатков. Оно применяется  для непрерывных и гладких функций в локальных интервалах задания. Для разрывных и периодически повторяющихся функций использовать его практически невозможно, равно как и для непрерывных не дифференцируемых функций. Кроме того, получаемые ряды могут сходиться очень медленно.

Самыми простыми способами интерполяции являются: интерполяция нулевого порядка, а также линейная и квадратичная интерполяции. При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. Графически это означает простое соединение узловых точек отрезками прямых. Зачастую также используется интерполяция нулевого порядка, когда уровень сигнала на интервале интерполяции соответствует последнему уровню исходного сигнала. Такой подход, например, реализуется в большинстве цифро-аналоговых преобразователей.

Линейная и квадратичная интерполяции являются частным случаем полиномиальной интерполяции с помощью аппроксимирующего полинома вида:

Для выполнения полиномиальной интерполяции достаточно по выражению (1) составить систему линейных уравнений для n узловых точек и определить n значений коэффициентов ai. При глобальной интерполяции, по всем N точкам задания функции, степень полинома равна N-1. Равномерной дискретизации данных для интерполяции не требуется. Максимальная степень полинома на практике обычно устанавливается не более 8-10, а большие массивы данных интерполируются последовательными локальными частями [4].

Для практического использования более удобны формулы аппроксимации, не требующие предварительного определения коэффициентов аппроксимирующих полиномов. К числу таких формул относится интерполяционный многочлен Лагранжа [5].

При сплайновой интерполяции обычно используются локальные полиномы не выше третьей степени. Так, например, кубические сплайны проходят через три смежные узловые точки (текущие опорные точки вычислений), при этом в граничных точках совпадают как значения полинома и функции, так и значения их первых и вторых производных. Коэффициенты полиномов, проходящих через три смежные узловые точки, рассчитываются так, чтобы непрерывными были первая и вторая его производные. Полиномы более высоких порядков чрезмерно громоздки для практики.

Сплайновая интерполяция может применяться для достаточно быстро изменяющихся функций, не имеющих разрывов функции и ее производных. Основной недостаток сплайнов – отсутствие единого аналитического выражения для описания функции. Кроме того, результаты сплайн интерполяции, существенно зависят от метода аппроксимации, и, соответственно, к их достоверности нужно подходить достаточно осторожно [4].

Общие недостатки интерполяции сугубо во временной области можно описать следующим образом:

- для каждого сигнала (участка сигнала) необходим индивидуальный подбор интерполирующей функции и интервала интерполяции;

- шумы, вызванные погрешностями интерполяции, в общем случае, являются плохо контролируемыми.

Постановка задач исследования. Для реализации восстановления сигналов из неравномерно распределенных отсчетов необходимо решить следующие задачи:

- обосновать выбор метода интерполяции;

- разработать алгоритм восстановления сигналов;

- минимизировать влияние алиасных компонент на восстановленный сигнал путем подбора параметров алгоритма восстановления.

Решение задач и результаты исследований.

В соответствии с предложенной структурой на первом этапе производиться преобразование неравномерно дискретизированного сигнала s(iΔt~) к сигналу с постоянным шагом дискретизации s(iΔt). Для выполнения данной процедуры можно использовать один из описанных выше методов интерполяции, либо применить метод, предполагающий вставку нулевых отсчетов вместо неизвестных [1]. Далее производится прямое интегральное преобразование, переводящее сигнал из временного представления в частотное. Как уже отмечалось, алисные компоненты при стохастической дискретизации имеют широкополосный шумоподобный спектр [1,3], и соответственно могут быть минимизированы путем пороговой обработки коэффициентов разложения S(f). После этого производится обратное преобразование, т.е. генерируется сигнал s*(iΔt) имеющий постоянный шаг дискретизации с уменьшенными уровнями алиасных компонент.

В качестве интегрального преобразования в данной структуре могут быть использованы дискретное преобразование Фурье (DFT) [1] или его разновидности дискретное косинусное преобразование (DCT) и дискретное синусное преобразование (DST). В рамках данного исследования был использован аппарат дискретного косинусного преобразования. Особенностью данного вида преобразования является то, что вычислительные операции производятся только с действительными числами, в отличие от дискретного преобразования Фурье. Прямое дискретное косинусное преобразование имеет вид [6]:

Результаты реализации данного алгоритма восстановления представлены на рисунке 2б. В качестве первичного сигнала использовалась последовательность треугольных импульсов (см. рис. 2а). Исходный стохастически дискретизированный сигнал s(iΔt~) формировался путем прореживания исходного равномерно дискретизированного сигнала. На рисунке 2 кружками отмечены отсчеты сигнала, выбранные в ходе прореживания. Шаг прореживания подчинялся равномерному закону распределения и изменялся дискретно в пределах от 1 до 16.

Как видно из сравнения рис. 2а и 2б в ходе реализации вышеописанного подхода наблюдаются значительные отличия формы восстановленного и первичного сигналов. Вызвано это тем, что компоненты полезного сигнала могут иметь уровень соизмеримый с алиасными компонентами и, соответственно, при пороговой обработке они теряются. Кроме того, при интегральных преобразованиях может быть искажена информация о фазе отдельных компонент исходного сигнала. Для минимизации данных эффектов было предложено использовать итерационный алгоритм удаления алиасных компонент [1] (см. рис. 3). Особенностью данного алгоритма является то, что порог отсечки рассчитывается на каждом цикле восстановления. Для корректного определения порога отсечки шумовых компонент необходимо учитывать априорную информацию о ширине спектра исходного сигнала. Эта информация используется для того, чтобы проводить анализ уровня алиасных компонент в спектральной области, где отсутствует исходный сигнал.

Благодаря этому в восстанавливаемом сигнале появляется высокочастотная область свободная от компонент исходного сигнала и содержащая только алиасный шум. По анализу уровня сигнала в данной области можно судить об общем уровне алиасного шума в сигнале и, соответственно, исходя из этого выбирать уровень порога отсечки.

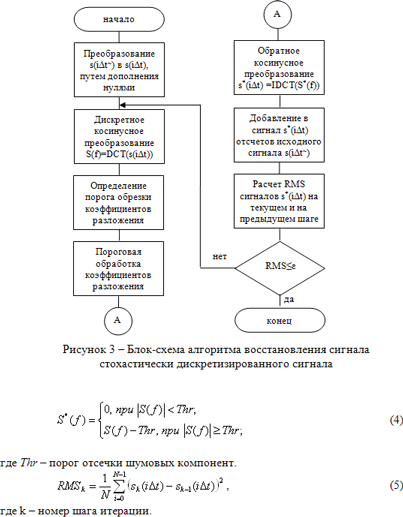
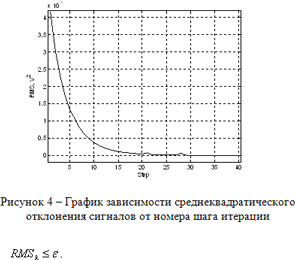
Процедура добавления отсчетов исходного сигнала в восстановленный сигнал позволяет повысить долю верных отсчетов в восстановленном сигнале и препятствует деградации процесса интерполяции [1]. Как показали результаты экспериментальных исследований, итерационный процесс восстановления является сходящимся и восстановленный сигнал достаточно точно воспроизводит форму первичного сигнала (см. рис. 2а и 2в). На рисунке 4 представлен график зависимости среднеквадратичного отклонения (RMS) восстанавливаемых сигналов на двух соседних итерационных шагах от номера итерации.

 Таким образом, в качестве критерия выхода из итерационного цикла может служить достижение среднеквадратическим отклонением значения заданной погрешности ε, т.е.

 В рамках данной работы исследования предложенного алгоритма проводились только для стационарных сигналов имеющих линейчатый спектр. При восстановлении стохастически дискретизированных нестационарных сигналов предложенный алгоритм имеет низкую эффективность. Это обусловлено тем, что при интегральном преобразовании происходит усреднение  характеристик сигнала, вследствие чего, теряются его локальные особенности, а при обрезке алиасных компонент могут быть потеряны шумоподобные компоненты сигнала. Для восстановления нестационарных сигналов наиболее целесообразно вместо интегрального преобразования использовать дискретное вейвлет преобразование [4].

Выводы.

1. Проведен аналитический обзор методов интерполяции стохастически дискретизированных сигналов.

2. Обоснована структура и принципы работы итерационного алгоритма восстановления стохастически дискретизированных стационарных сигналов, который отличается от существующих способом минимизации алисных компонент и критерием завершения итерационного цикла.

3. Проведено исследование разработанного алгоритма и показа устойчивость его работы и высокое качество восстановления стационарных сигналов.

Литература

1. Bilinskis I. Digital alias-free signal processing. – Wiliy, 2007. – 430 p.

2. Дмитриев В.И. Прикладная теория информации: Учебник для вузов.- М.: ВШ, 1989.

3. Beutler F.  Alias-free randomly timed sampling of stochastic processes. — IEEE Trans. Inf. Theory, Vol. IT- 16, No. 2, 1970. pp. 147–152.

4. Дьяконов В.П. Вейвлеты. От теории к практике. – М.: СОЛОН-Р, 2002. – 448 с.

5. Корн Г., Корн Е. Справочник по математике для научных работников и инженеров. – М.: Наука, 1984.

<<назад