Силовые характеристики процесса резания в значительной мере определяют
эффективность эксплуатации режущего инструмента. Современные тенденции роста производительности за счет
повышения режимов механической обработки приводят к существенному увеличению нагрузок на режущий инструмент, в
связи с чем растет и актуальность задач по их исследованию.
В настоящее время вопросы определения сил резания достаточно хорошо
проработаны. В результате теоретических исследований, основанных, прежде всего, на работах Зорева Н.Н. [1, 2],
созданы аналитические модели определения сил в зоне стружкообразования, на передней и задней поверхностях
лезвия инструмента. На основании многочисленных экспериментальных исследований разработана
справочно-нормативная база для расчета сил резания в различных условиях механообработки. Современные
исследования закономерностей функционирования режущего инструмента развиваются в направлении математического
моделирования процесса резания, и в первую очередь - моделирования нагрузок, действующих на лезвие инструмента
[3, 4].
Силы, действующие на передней и задней поверхностях лезвия режущего
элемента, отличаются друг от друга по величине и направлению. Как правило, силы на задней поверхности малы по
сравнению с силами на передней поверхности. Поэтому при рассмотрении баланса сил, действующих в процессе
резания, силами на задней поверхности, часто пренебрегают. В связи с этим вопросам определения сил на задней
поверхности уделяется значительно меньшее внимание, чем на передней, удобные для использования методики их
расчета практически отсутствуют.
Однако при значительном износе силы на задних поверхностях могут быть
велики, и даже превышать силы на передней поверхности. В таких случаях даже приближенный анализ баланса сил,
действующих в процессе резания, становится невозможным без учета сил на задней поверхности. Определение
контактных усилий по задней поверхности инструмента с использованием численных методов расчета [5] весьма
затруднительно для широкого диапазона условий механообработки.
Целью настоящей работы является исследование закономерностей формирования
сил на задней поверхности лезвия инструмента и создание удобной для практического применения аналитической
методики их определения.
В процессе резания задняя поверхность инструмента соприкасается с
обрабатываемым материалом и подвергается износу, причем режущая кромка несколько закругляется. Площадь
образующейся фаски износа определяет площадь контакта задней поверхности с обрабатываемым материалом.
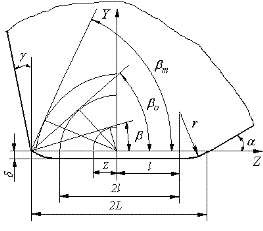
Схематически профиль изношенной задней поверхности инструмента представлен на рис. 1. Полагается, что профиль
задней поверхности является симметричным относительно центра фаски износа и что кривизной поверхности резания
можно пренебречь [1].

| Рисунок 1 - Схематическое изображение профиля изношенной задней поверхности лезвия инструмента. |
где L - полуширина контакта задней поверхности с обрабатываемым материалом, или полуширина фаски износа
задней поверхности; l – полудлина плоской части фаски износа; r – радиус кривизны краев фаски
износа задней поверхности; 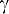 ,
,  – передний и задний
углы лезвия инструмента соответственно;
– передний и задний
углы лезвия инструмента соответственно;  – глубина внедрения задней поверхности
лезвия в обрабатываемую деталь; Z - абсцисса рассматриваемой точки на поверхности контакта, или
расстояние рассматриваемой точки от середины ширины контакта;
– глубина внедрения задней поверхности
лезвия в обрабатываемую деталь; Z - абсцисса рассматриваемой точки на поверхности контакта, или
расстояние рассматриваемой точки от середины ширины контакта;  0,
0,
 - вспомогательные параметры, которые определяются следующим образом:
- вспомогательные параметры, которые определяются следующим образом:

Контакт задней поверхности с обрабатываемым материалом в основном можно
считать упругим, так как условие пластичности выполняется только у режущей кромки, где контактные напряжения
достигают максимума. Такие условия контакта можно рассматривать как случай вдавливания узкого длинного штампа
с округленными краями, вблизи которых обрабатываемый материал переходит в пластичное состояние. Выражение для
нормального давления на поверхности контакта имеет вид:

где N – равнодействующая нормальная сила на задней поверхности.
При некотором значении  =
=
 m давление р будет максимальным. Значение
m давление р будет максимальным. Значение
 m может быть получено путем дифференцирования выражения (2)
из условия dp/d
m может быть получено путем дифференцирования выражения (2)
из условия dp/d = 0, что обеспечивается соотношением:
= 0, что обеспечивается соотношением:

При известном значении  0
может быть определено значение
0
может быть определено значение  m. В большинстве случаев
значение
m. В большинстве случаев
значение  0 неизвестно и требует специальных методов расчета.
Методика одновременного определения как
0 неизвестно и требует специальных методов расчета.
Методика одновременного определения как  0, так и
0, так и
 m заключается в следующем. Путем подстановки в выражение (2)
m заключается в следующем. Путем подстановки в выражение (2)
 m вместо
m вместо  определяется
максимальное значение нормального давления на поверхности контакта рm. С другой стороны
максимальное значение рm имеет место в точке перехода задней поверхности в переднюю, где
удовлетворяется условие пластичности и, следовательно, рm связано с сопротивлением
обрабатываемого материала сдвигу в условиях резания -
определяется
максимальное значение нормального давления на поверхности контакта рm. С другой стороны
максимальное значение рm имеет место в точке перехода задней поверхности в переднюю, где
удовлетворяется условие пластичности и, следовательно, рm связано с сопротивлением
обрабатываемого материала сдвигу в условиях резания - 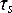 и коэффициентом трения
по задней поверхности лезвия
и коэффициентом трения
по задней поверхности лезвия  . Согласно [1], эта связь имеет вид:
. Согласно [1], эта связь имеет вид:
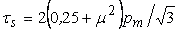 .
.
Отсюда может быть получено следующее выражение:

где  1, Е1 - упругие константы
обрабатываемого материала;
1, Е1 - упругие константы
обрабатываемого материала;  2, Е2 - упругие
константы материала инструмента; В - кривизна краев фаски износа задней поверхности
B = 1/r;
2, Е2 - упругие
константы материала инструмента; В - кривизна краев фаски износа задней поверхности
B = 1/r; 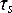 - предел текучести на сдвиг обрабатываемого материала.
- предел текучести на сдвиг обрабатываемого материала.
Значения углов  0 и
0 и
 m определяются из совместного решения уравнений (3) и (4).
Получение решения в аналитическом виде весьма затруднительно, в связи с чем используются численные методы
расчета.
m определяются из совместного решения уравнений (3) и (4).
Получение решения в аналитическом виде весьма затруднительно, в связи с чем используются численные методы
расчета.
В результате решения указанной системы уравнений установлена зависимость
параметров  0 и
0 и  m
от величины фаски износа L, представленная на рис. 2.
m
от величины фаски износа L, представленная на рис. 2.

Рисунок 2 - Графики зависимости параметров  0
и 0
и  m от величины фаски износа L. m от величины фаски износа L. |
Расчеты выполнены для условий обработки конструкционных сталей
твердосплавными инструментами (принятые параметры: 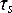 = 450МПа;
= 450МПа;
 1 = 0,25; Е1 = 2,1
1 = 0,25; Е1 = 2,1 10
10 МПа;
МПа;
 2 = 0,25; Е2 = 5,0
2 = 0,25; Е2 = 5,0 10
10 МПа;
МПа;
 = 0,5; В = 0,1). Из графиков следует, что с увеличением износа параметры
= 0,5; В = 0,1). Из графиков следует, что с увеличением износа параметры
 0 и
0 и  m
увеличиваются, причем их наиболее интенсивный рост наблюдается в области малых значений износа. Зная
m
увеличиваются, причем их наиболее интенсивный рост наблюдается в области малых значений износа. Зная
 0 и
0 и  m, можно
определить нормальную силу на задней поверхности N для любых значений износа [1]:
m, можно
определить нормальную силу на задней поверхности N для любых значений износа [1]:

где b - длина контакта задней поверхности с обрабатываем материалом, или ширина среза.
Для расчета нормальной силы на задней поверхности N целесообразно
установить закономерности изменения безразмерного коэффициента K, входящего в формулу расчета (5),
зависящего только от параметров  0 и
0 и
 m:
m:

График изменения безразмерного коэффициента KТ,
теоретически рассчитанного по формуле (6) в зависимости от величины фаски износа L с учетом
соответствующего изменения параметров  0 и
0 и
 m, представлен на рис.3.
m, представлен на рис.3.
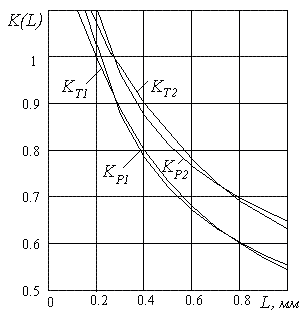
| Рисунок 3 - Графики зависимости коэффициента K от величины фаски износа L для инструментов, оснащенных твердым сплавом - 1 и быстрорежущей сталью - 2. |
При расчетах учтено различие в свойствах различных инструментальных
материалов: модуль упругости для быстрорежущих сталей Е2бр = 2,1 10
10 МПа
отличается от модуля упругости для твердых сплавов, вследствие чего изменяются параметры
МПа
отличается от модуля упругости для твердых сплавов, вследствие чего изменяются параметры
 0 и
0 и  m, а
следовательно и коэффициенты KТ. Графики зависимости коэффициента KТ от
величины фаски износа L для инструментов, оснащенных твердым сплавом KТ1 и
быстрорежущей сталью KТ2, представлены на рис. 3.
m, а
следовательно и коэффициенты KТ. Графики зависимости коэффициента KТ от
величины фаски износа L для инструментов, оснащенных твердым сплавом KТ1 и
быстрорежущей сталью KТ2, представлены на рис. 3.
Для практического использования целесообразно, пользуясь методикой
регрессионного анализа, упростить выражение (6). С достаточной точностью (до 5%) взаимосвязь коэффициентов
KP1 и KP2 с величиной фаски износа по задней поверхности L для
инструментов, оснащенных твердым сплавом и быстрорежущей сталью, может быть выражена следующими
зависимостями:
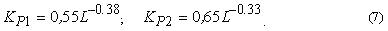
Графики зависимости коэффициентов KP1 и KP2 от величины фаски износа L, также представленные на рис. 3, достаточно близки к графикам KT1 и KT2. Графики свидетельствуют о том, что с увеличением фаски износа по задней поверхности коэффициент K(L) снижается.
В результате исследований установлено, что параметры
 0 и
0 и  m
зависят от коэффициента трения по задней поверхности лезвия
m
зависят от коэффициента трения по задней поверхности лезвия  , вследствие чего
изменяется и коэффициент KТ, рассчитываемый по формуле (6). Графики зависимости
коэффициента K(
, вследствие чего
изменяется и коэффициент KТ, рассчитываемый по формуле (6). Графики зависимости
коэффициента K( ) от величины коэффициента трения
) от величины коэффициента трения
 для инструментов, оснащенных твердым сплавом, при различных значениях износа
h (K
для инструментов, оснащенных твердым сплавом, при различных значениях износа
h (K 1 - h1 = 1мм,
K
1 - h1 = 1мм,
K 2 - h2 = 0,5мм,
K
2 - h2 = 0,5мм,
K 3 - h3 = 0,2мм) представлены на рис. 4.
3 - h3 = 0,2мм) представлены на рис. 4.

Рисунок 4 - Графики зависимости коэффициента K от величины коэффициента трения
 при различных значениях износа h. при различных значениях износа h. |
Из графиков следует, что с увеличением коэффициента трения
 коэффициент K(
коэффициент K( ) снижается для всех
значений износа.
) снижается для всех
значений износа.
С достаточной точностью (до 5%) взаимосвязь коэффициентов
K( ) с величиной коэффициента трения
) с величиной коэффициента трения  может
быть выражена следующими зависимостями:
может
быть выражена следующими зависимостями:
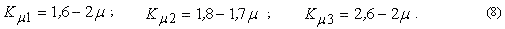
На основании выполненных исследований зависимость для расчета нормальной
силы на задней поверхности NР, с учетом соответствующих условий для определения коэффициента
KT по (7) и (8), может быть выражена следующим образом:

Адекватность полученной зависимости подтверждена результатами
экспериментальных исследований, представленных в работе [1]. Условия проведения экспериментальных исследований
и расчетов: обрабатываемый материал – сталь 20Х; 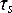 = 380МПа;
= 380МПа;
 1 = 0,25;
Е1 = 2,1
1 = 0,25;
Е1 = 2,1 10
10 МПа;
инструментальный материал - быстрорежущая сталь; ширина среза b = 10мм; скорость резания
V = 0,7 м/мин. Результаты экспериментов по влиянию износа h на нормальную силу на задней
поверхности N, представленные графиком NЭ для коэффициента трения
МПа;
инструментальный материал - быстрорежущая сталь; ширина среза b = 10мм; скорость резания
V = 0,7 м/мин. Результаты экспериментов по влиянию износа h на нормальную силу на задней
поверхности N, представленные графиком NЭ для коэффициента трения
 = 0,35, достаточно хорошо (погрешность не превышает 10%) совпадают с
рассчитанным для тех же условий графиком NР1 на рис.5.
= 0,35, достаточно хорошо (погрешность не превышает 10%) совпадают с
рассчитанным для тех же условий графиком NР1 на рис.5.

Рисунок 5 - Графики зависимости нормальной силы на задней поверхности лезвия N от
износа h при различных коэффициентах трения  . . |
Результаты экспериментов по определению нормальной силы N при
износе h = 0,1мм для различных коэффициентов трения  , представленные на
рис.5 точками 1,2,3 (соответственно
, представленные на
рис.5 точками 1,2,3 (соответственно  1 = 1,9,
1 = 1,9,
 2 = 0,35,
2 = 0,35,
 3 = 0,1), также хорошо совпадают с расчетными значениями на
графиках NP1, NP2, NP3. Результаты сравнения
подтверждают возможность использования полученных зависимостей для расчета сил на задней поверхности лезвия
инструмента.
3 = 0,1), также хорошо совпадают с расчетными значениями на
графиках NP1, NP2, NP3. Результаты сравнения
подтверждают возможность использования полученных зависимостей для расчета сил на задней поверхности лезвия
инструмента.
Таким образом, в результате исследований закономерностей формирования сил на задней поверхности лезвия инструмента разработана и экспериментально подтверждена методика их расчета, содержащая в удобном для практического применения виде поправочные коэффициенты для учета различных условий механообработки. Методика может быть использована для прогнозирования сил резания в зависимости от величины износа задней поверхности лезвия инструмента и обоснования силовых критериев затупления инструмента при различных видах обработки.
Зорев Н.Н. Вопросы механики процесса резания металлов. - М.: Машгиз, 1956. - 366с.
Развитие науки о резании металлов. - М.: Машиностроение, 1967. - 416 с.
Струтинській В.Б. Математичне моделювання процесів та систем механіки. Житомир: ЖІТІ, 2001. – 612 с.
Ю.В. Петраков. Моделирование процессов обработки резанием // Сучасні технології машинобудування: Збірник наукових статей / За заг. ред. А.І. Грабченка. В 2-х т. – Харків: НТУ «ХПІ», 2006. Т. 2. – с. 221 - 232.
Татьянченко А.Г., Малышко И.А. Определение контактных усилий по задней поверхности инструмента при развертывании // Прогрессивные технологии и системы машиностроения. Международный сборник научных трудов. - Донецк: ДонНТУ, 2002. - Вып. 19. - с. 239 - 245.
 |