1 Введение
1.1 Актуальность проблемы
Тепловые процессы при резании в значительной мере определяют операции
обработки в технологических системах, оказывая существенное влияние на функциональную способность режущего
инструмента и качество обработки. Контроль тепловых процессов при резании является одним из условий повышения
эффективности эксплуатации режущего инструмента, обеспечивая повышение его надежности, производительности и
качества обработки.
Использование смазочно-охлаждающих технологических сред – наиболее эффективный способ контроля тепловых явлений, обеспечивающий уменьшение температуры при резании и повышающий
производительность и качество обработки.
Теоретически средство для исследования конвективного тепла
характеризуется коэффициентом теплопроводности, который довольно подробно описан в [1]. Однако нормативы по
выбору коэффициента теплопроводности для составляющих технологических систем практически отсутствуют.
Доступная информация о закономерностях его изменения в зависимости от условий обработки не содержит информацию
относительно влияния коэффициента теплопроводности на температуру резания, что не позволяет управлять
тепловыми процессами при резании [2].
Сейчас для охлаждения режущего инструмента используются составы на основе
водных растворов, которые по своим свойствам близки к свойствам воды. При обработке наиболее распространенным
способом жидкостного охлаждения является омывание свободно текущей струей жидкости [3]. На практике в данном
направлении приведено влияние способов жидкостного охлаждения на коэффициент теплопроводности и обоснование
возможностей его изменения.
Цель представляемой работы – комплексное исследование взаимосвязи
температуры резания со способами жидкостного охлаждения и коэффициентом теплопроводности, а также разработка
основополагающей теории контроля тепловых процессов при резании.
1.2 Формулирование задач исследования
Теоретической основой контроля температуры резания в представленной работе
является аналитическое рассмотрение теплового состояния сборного режущего инструмента с механическим
креплением твердосплавных пластин, зависящего от параметров процесса резания и условий конвективного
теплообмена с окружающей средой.
Теоретические исследования тепловых процессов в режущем инструменте
используются для решения следующих задач:
аналитическое определение температурного поля на режущей кромке инструмента и
температуры резания;
исследование влияния способов жидкостного охлаждения на коэффициент теплопроводности и
обоснование возможностей его изменения в данном направлении;
определение природы и уровня влияния коэффициента теплопроводности на температуру
резания.
2 Теоретические исследования
2.1 Определение температурного поля на режущей кромке инструмента и
температуры резания
Температурное поле на режущей кромке инструмента возрастает под действием
источника тепла, который возникает в месте контакта стружки с передней поверхностью, и описывается в следующем
виде [1]:

где 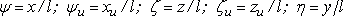 - безразмерные координаты;
- безразмерные координаты; 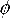 =
0,5b/l - безразмерная ширина среза; l - длина площадки контакта в направлении схода стружки;
b - ширина среза; х, y, z – координаты точек режущей кромки;
хи, zи – координаты источника;
=
0,5b/l - безразмерная ширина среза; l - длина площадки контакта в направлении схода стружки;
b - ширина среза; х, y, z – координаты точек режущей кромки;
хи, zи – координаты источника;  - теплопроводность
материала инструмента; K
- теплопроводность
материала инструмента; K - переводной коэффициент от
безразмерных величин к размерным; Т(
- переводной коэффициент от
безразмерных величин к размерным; Т( ,
,
 ,
,  ) - безразмерное температурное поле;
P - размерный коэффициент; q - функция плотности теплового потока.
) - безразмерное температурное поле;
P - размерный коэффициент; q - функция плотности теплового потока.
Безразмерное температурное поле на режущей кромке инструмента представлено
на рисунке 1.

|
Рисунок 1 - Безразмерное температурное поле на режущей кромке инструмента |
|
Температура резания рассчитывается по следующей формуле:

где  - безразмерное выражение износа по боковой поверхности h:
- безразмерное выражение износа по боковой поверхности h:
 = h/l; ТР - безразмерная температура резания.
= h/l; ТР - безразмерная температура резания.
Графики зависимости безразмерной температуры резания от безразмерного
выражения износа по боковой поверхности  и безразмерной ширины среза
и безразмерной ширины среза
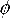 представлены на рисунке 2.
представлены на рисунке 2.

|
Рисунок 2 - Графики зависимости безразмерной температуры резания от безразмерного
выражения износа по боковой поверхности  и безразмерной
ширины среза и безразмерной
ширины среза 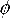 . . |
|
Графики зависимости безразмерной температуры резания от
безразмерного выражения износа по боковой поверхности  и безразмерной ширины
среза
и безразмерной ширины
среза 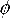 в двойной логарифмической системе координат представлены на
рисунке 3.
в двойной логарифмической системе координат представлены на
рисунке 3.
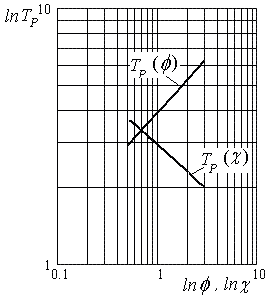
|
Рисунок 3 - Графики зависимости безразмерной температуры резания от безразмерного выражения
износа по боковой поверхности  и безразмерной ширины среза и безразмерной ширины среза
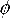 в двойной логарифмической системе координат в двойной логарифмической системе координат |
|
На практике используется упрощенная модель расчета безразмерной
температуры резания:

Описание температурного поля
Т( ,
,  ,
,
 ) и температуры резания ТР в безразмерном виде позволяет
установить общую закономерность температурных колебаний, которые в данном процессе корректируются размерным
коэффициентом
) и температуры резания ТР в безразмерном виде позволяет
установить общую закономерность температурных колебаний, которые в данном процессе корректируются размерным
коэффициентом  , принятым, исходя из расчетных свойств инструмента и условий
его применения.
, принятым, исходя из расчетных свойств инструмента и условий
его применения.
Распределение температур по передней поверхности инструмента в
плоскости, перпендикулярной главной режущей кромке, для различных инструментальных материалов представлено на
рисунке 4.
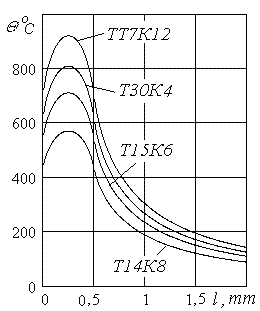
|
Рисунок 4 - Распределение температур по передней поверхности на режущей кромке резцов с
различными твердосплавными пластинами |
|
Расчеты температур для резцов, оснащенных твердосплавными
пластинами (Т14К8 -  = 33,9Вт/м
= 33,9Вт/м

 С, Т15К6 -
С, Т15К6 -
 = 27,2Вт/м
= 27,2Вт/м
 С, Т30К4 -
С, Т30К4 -  = 23,9Вт/м
= 23,9Вт/м

 С, ТТ7К12 -
С, ТТ7К12 -
 = 20,9Вт/м
= 20,9Вт/м
 С), выполнены для следующих условий: обрабатываемый материал – сталь 45,
С), выполнены для следующих условий: обрабатываемый материал – сталь 45,
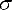 = 750МПа, режимы резания – глубина резания t = 2мм,
подача s = 0,4мм/об., скорость резания v = 120 м/мин., износ по задней поверхности
h = 0,9мм. Геометрические параметры резца: углы в плане
= 750МПа, режимы резания – глубина резания t = 2мм,
подача s = 0,4мм/об., скорость резания v = 120 м/мин., износ по задней поверхности
h = 0,9мм. Геометрические параметры резца: углы в плане
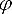 =
= 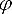 1 = 45°, передний угол
1 = 45°, передний угол
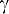 = -5°, задний угол
= -5°, задний угол  = 5°. Для этих условий:
l = 0,45мм, q = 2,37
= 5°. Для этих условий:
l = 0,45мм, q = 2,37 10
10 Вт
/м
Вт
/м .
.
Результаты расчета температур на передней поверхности резца для
различных инструментальных материалов выявляют существенные различия температур, зависящих от свойств
инструментальных материалов и условий резания.
Максимальная температура достигается при значениях
 = 0,5;
= 0,5;  = 0 и рассчитывается следующим
образом:
= 0 и рассчитывается следующим
образом:
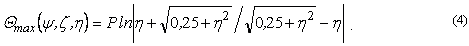
Максимальная температура создает необходимость использования
смазочно-охлаждающих технологических сред.
2.2 Исследование влияния способов жидкостного охлаждения на
коэффициент теплопроводности
Вторым этапом является исследование влияния способов жидкостного
охлаждения на коэффициент теплопроводности для наиболее распространенных способов подачи жидкости в зону
резания – свободное омывание, разбрызгивание под напором и распыление.
При подаче жидкости в зону резания свободным омыванием для определения
коэффициента теплопроводности используется критериальное уравнение [1]:
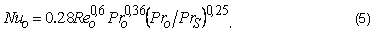
где 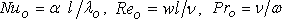 - безразмерные критерии Нуссельта, Рейнольдса и Прандтля соответственно;
l - базовый размер;
- безразмерные критерии Нуссельта, Рейнольдса и Прандтля соответственно;
l - базовый размер;  0 - теплопроводность жидкости;
w - скорость потока;
0 - теплопроводность жидкости;
w - скорость потока;  - кинематический коэффициент вязкости среды;
- кинематический коэффициент вязкости среды;
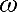 - тепловая диффузия.
- тепловая диффузия.
Коэффициент теплопроводности устанавливается, исходя из равенства для
охлаждения жидким раствором (3 - 5 % эмульсии):
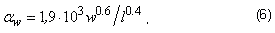
где l = BH/2(B+H) - рассчитано при условии рассечения телом потока жидкости;
B, Н - размеры инструмента.
С учетом того, что скорость потока жидкости w =
4 103R/60
103R/60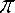 d2,
определяется ее расход R и диаметр сопла d, из которого она выходит, и коэффициент
теплопроводности равен:
d2,
определяется ее расход R и диаметр сопла d, из которого она выходит, и коэффициент
теплопроводности равен:
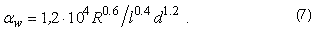
При подаче жидкости в зону резания разбрызгиванием под напором для
определения коэффициента теплопроводности используется критериальное уравнение:

Коэффициент теплопроводности устанавливается из равенства:

где базовый размер l = Н.
Учитывая скорость потока жидкости, коэффициент теплопроводности
равен:

При подаче жидкости в зону резания распылением коэффициент
теплопроводности равен:

где K – концентрация жидкости в двухфазной воздушно-жидкостной среде,
m = 6,  a - коэффициент теплопроводности в воздухе:
a - коэффициент теплопроводности в воздухе:

2.3 Определение сущности и уровня влияния коэффициента
теплопроводности на температуру резания
Следующим этапом является определение природы и уровня влияния
коэффициента теплопроводности на температуру резания.
В результате исследований наиболее распространенных способов подачи
жидкости в зону резания подтверждаются следующие взаимосвязи коэффициента уменьшения температуры резания
КQ с коэффициентом теплопроводности:
распыление

разбрызгивание под напором

свободное омывание

При подаче жидкости свободным омыванием с учетом коэффициента понижения
температуры резания КQw (7) приобретает вид:
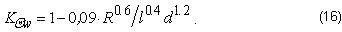
Полученное выражение позволяет предвидеть уровень понижения
температуры резания в зависимости от способа подачи жидкости в зону резания.
Графики зависимости коэффициента понижения температуры резания
КQw (линии уровня, на которых числами показаны значения коэффициента) от расхода жидкости R
и диаметра сопла d для ВхН = 20х25мм2 представлены на рисунке 5.

|
Рисунок 5 - Графики зависимости коэффициента понижения температуры резания
КQw от расхода жидкости R и диаметра сопла d |
|
В основе представленных графиков для указанных значений коэффициента
КQw лежат способы жидкостного охлаждения, обеспечивающие требуемую температуру резания.
3 Экспериментальные исследования
Экспериментальные исследования температуры резания используются для
обоснования соответствующих теоретических моделей.
Экспериментальные исследования и расчеты температуры для резцов с другими
инструментальными материалами выполнены для следующих условий: обрабатываемый материал – сталь 45, режимы
резания – глубина резания t = 1мм, подача s = 0,1мм/об., скорость резания v =
120 м/мин., износ кромки по задней поверхности h = 0,4мм.
Сборный режущий инструмент с механическим креплением твердосплавных
пластин Т15К6 имеет следующие геометрические параметры: углы в плане
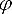 =
= 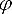 1 = 45°, передний угол
1 = 45°, передний угол
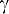 = -5°, задний угол
= -5°, задний угол  = 5°.
= 5°.

|
Рисунок 6 - Теоретические и экспериментальные графики зависимости температуры резания от
скорости резания v – а) и от подачи s – б) |
|
Экспериментальные результаты (график 2) довольно точно совпадают с
теоретическими (график 1). Параметры теоретических режимов подтверждаются и отличаются от экспериментальных на
10%, что доказывает правильность соответствующих теоретических моделей.
4 Заключение
Разработанная методика аналитического определения температурного поля на
режущей кромке инструмента и температуры резания позволяет регулировать данный уровень температур, расширяя
выбор рациональных условий обработки, и позволяет определять необходимость использования смазочно-охлаждающих
технологических сред.
Разработанная методика применяется для определения температурного поля
различных инструментов. Установленные на примере резцов законы влияния геометрических параметров на
распределение температур по передней поверхности могут распространяться на другие инструменты. Особенности
различных видов обработки учитываются при расчете плотности тепловых потоков и длины контакта стружки с
передней поверхностью. На основе полученных результатов разработаны рекомендации по выбору инструментальных
материалов и рациональных параметров инструмента.
Для наиболее распространенных способов подачи жидкости в зону резания -
свободное омывание, разбрызгивание под напором и распыление, регулирующие основное состояние подачи жидкости
– расход и скорость определяют любой данный коэффициент теплопроводности.
Результат исследования взаимосвязи коэффициента уменьшения температуры
резания с коэффициентом теплопроводности подтверждается различными способами подачи жидкости в зону резания,
которые позволяют получать любой данный уровень температуры резания, расширяя выбор соответствующих
коэффициентов теплопроводности и условий подачи жидкости.
Разработанная методика используется для анализа температуры резания при
чистовом и тонком точении резцами, оснащенными твердым сплавом. С учетом установленных температурных
ограничений метод линейного программирования позволят определять оптимальные режимы чистового и тонкого
точения, обеспечивая максимальную производительность. Это означает, что при уменьшении температуры резания и
изменении температурных ограничений применение охлаждающей жидкости с регулируемыми способами подачи в зону
резания обеспечивает повышение производительности обработки в 1,5 – 3 раза.
Таким образом, в результате проведенного комплекса исследований
установлены взаимосвязи температуры резания со способами подачи жидкости и коэффициентом теплопроводности,
созданные на основе фундаментальной теории контроля тепловых процессов при резании.
Литература
Резников А.Н., Резников Л.А. Тепловые процессы в технологических системах. - М.:
Машиностроение, 1990. – 288с.
Iвченко Т.Г. Аналітичне визначення температури різання в залежності від умов
експлуатації ріжучого інструменту // Наукові праці Донецького національного технічного університету.
Серія: Машинобудування і машинознавство. Випуск 92. - Донецьк, ДонНТУ, 2005.- С.37-42.
Івченко Т.Г., Нечепаєв В.Г., Гнитько, О.М. Вплив способу подачі охолоджуючого
середовища на температуру різання // Надійність інструменту та оптимізація технологічних систем.
Збірник наукових праць. Вип. 16 . – Краматорськ: ДДМА, 2005. - с.34 - 38.
Электронная библиотека

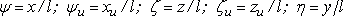 - безразмерные координаты;
- безразмерные координаты; 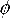 =
0,5b/l - безразмерная ширина среза; l - длина площадки контакта в направлении схода стружки;
b - ширина среза; х, y, z – координаты точек режущей кромки;
хи, zи – координаты источника;
=
0,5b/l - безразмерная ширина среза; l - длина площадки контакта в направлении схода стружки;
b - ширина среза; х, y, z – координаты точек режущей кромки;
хи, zи – координаты источника;  - теплопроводность
материала инструмента; K
- теплопроводность
материала инструмента; K - переводной коэффициент от
безразмерных величин к размерным; Т(
- переводной коэффициент от
безразмерных величин к размерным; Т( ,
,
 ,
,  ) - безразмерное температурное поле;
P - размерный коэффициент; q - функция плотности теплового потока.
) - безразмерное температурное поле;
P - размерный коэффициент; q - функция плотности теплового потока.

 - безразмерное выражение износа по боковой поверхности h:
- безразмерное выражение износа по боковой поверхности h:
 = h/l; ТР - безразмерная температура резания.
= h/l; ТР - безразмерная температура резания. и безразмерной ширины среза
и безразмерной ширины среза
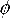 представлены на рисунке 2.
представлены на рисунке 2.
 и безразмерной
ширины среза
и безразмерной
ширины среза 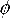 .
. и безразмерной ширины
среза
и безразмерной ширины
среза 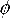 в двойной логарифмической системе координат представлены на
рисунке 3.
в двойной логарифмической системе координат представлены на
рисунке 3.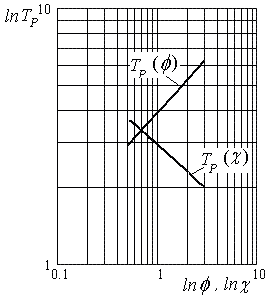
 и безразмерной ширины среза
и безразмерной ширины среза
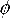 в двойной логарифмической системе координат
в двойной логарифмической системе координат
 ,
,  ,
,
 ) и температуры резания ТР в безразмерном виде позволяет
установить общую закономерность температурных колебаний, которые в данном процессе корректируются размерным
коэффициентом
) и температуры резания ТР в безразмерном виде позволяет
установить общую закономерность температурных колебаний, которые в данном процессе корректируются размерным
коэффициентом  , принятым, исходя из расчетных свойств инструмента и условий
его применения.
, принятым, исходя из расчетных свойств инструмента и условий
его применения.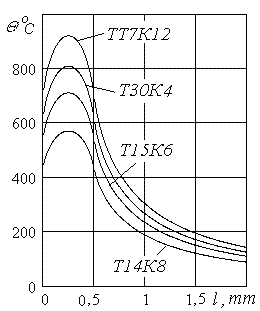
 = 33,9Вт/м
= 33,9Вт/м

 С, Т15К6 -
С, Т15К6 -
 = 27,2Вт/м
= 27,2Вт/м
 С, Т30К4 -
С, Т30К4 -  = 23,9Вт/м
= 23,9Вт/м

 С, ТТ7К12 -
С, ТТ7К12 -
 = 20,9Вт/м
= 20,9Вт/м
 С), выполнены для следующих условий: обрабатываемый материал – сталь 45,
С), выполнены для следующих условий: обрабатываемый материал – сталь 45,
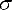 = 750МПа, режимы резания – глубина резания t = 2мм,
подача s = 0,4мм/об., скорость резания v = 120 м/мин., износ по задней поверхности
h = 0,9мм. Геометрические параметры резца: углы в плане
= 750МПа, режимы резания – глубина резания t = 2мм,
подача s = 0,4мм/об., скорость резания v = 120 м/мин., износ по задней поверхности
h = 0,9мм. Геометрические параметры резца: углы в плане
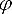 =
= 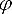 1 = 45°, передний угол
1 = 45°, передний угол
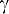 = -5°, задний угол
= -5°, задний угол  = 5°. Для этих условий:
l = 0,45мм, q = 2,37
= 5°. Для этих условий:
l = 0,45мм, q = 2,37 10
10 Вт
/м
Вт
/м .
. = 0,5;
= 0,5;  = 0 и рассчитывается следующим
образом:
= 0 и рассчитывается следующим
образом: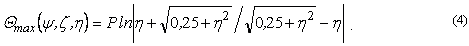
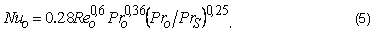
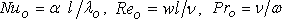 - безразмерные критерии Нуссельта, Рейнольдса и Прандтля соответственно;
l - базовый размер;
- безразмерные критерии Нуссельта, Рейнольдса и Прандтля соответственно;
l - базовый размер;  0 - теплопроводность жидкости;
w - скорость потока;
0 - теплопроводность жидкости;
w - скорость потока;  - кинематический коэффициент вязкости среды;
- кинематический коэффициент вязкости среды;
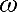 - тепловая диффузия.
- тепловая диффузия.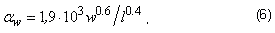
 103R/60
103R/60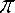 d2,
определяется ее расход R и диаметр сопла d, из которого она выходит, и коэффициент
теплопроводности равен:
d2,
определяется ее расход R и диаметр сопла d, из которого она выходит, и коэффициент
теплопроводности равен: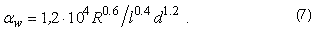




 a - коэффициент теплопроводности в воздухе:
a - коэффициент теплопроводности в воздухе: