Традиционный анализ структуры поверхности включает в себя разложение профилей поверхности на различные диапазоны с разной длиной волны, которые обычно трактуются как шероховатость, волнистость и форма. Основной целью разложения профилей поверхности является описание каждого диапазона для технологического процесса, в ходе которого получился этот участок поверхности и ожидаемые эксплуатационные качества этого компонента. Современные тенденции производства направлены на снижение допусков и повышение стандартов изготовления, что требует тщательного отслеживания процесса изготовления. Соответственно, существует необходимость в более точном определении полосы частот для отображения процессов функциональной взаимосвязи. Вейвлеты становятся все более широко используемым средством для эффективного разложения профилей на множество диапазонов. В то время, как вейвлеты позиционируются как имеющие значительное преимущество перед традиционным разложением, фундаментальные вопросы, такие как выбор вейвлетных базисов, остаются нерассмотренными. Основная цель данной работы – показать различия между вейвлетами характеристиках передачи связанных с ними фильтрующих блоков, что является существенным для анализа поверхности.
      В работе делается обзор основных математических процессов теории вейвлетов, необходимой для применения вейвлетов для анализа структуры поверхности. В данной работе изучаются вейвлеты двух основных видов – ортогональные и биортогональные вейвлетные базисы, сравниваются фильтрующие блоки, соответствующие данным вейвлетам и выполняется анализ множественного разложения профилей поверхности.
       Типичная техническая поверхность состоит из ряда пространственных частот. Высокочастотные или с короткой длиной волны компоненты называются шероховатостью, средней частоты – волнистостью, а низкочастотные компоненты – формой.
      Исторически сложилось так, различные аспекты технологического процесса создают различные режимы длины волны, а они влияют по-разному на функцию детали. Разделяя поверхность профиля на различные диапазоны, становится возможным составить план частотного спектра каждого диапазона для технологического процесса с помощью которого он был создан, или же же специфических функциональных аспектов детали. Таким образом, разделение профилей поверхности служит удобным инструментом для процесса контроля и функциональной корреляции.
      Основным результатом данного подхода к разделению и расчетов параметров является деление большого волнового диапазона на единые блоки, такие как шероховатость, волнистость, форма. Текущее состояние дел в разделении структуры поверхности ограничивается получением параметров, которые являются усредненными для большого режима длины волны, пример – шероховатость. Фильтр Гаусса, вероятно наиболее используемый сегодня в поверхностной метрологии, неспособен разделить профиль на четкие полосы частот из-за характеристик его передачи. Так как современные тенденции производства направлены на лучшую обработку, увеличение гарантийных сроков службы изделия и сужение допусков, то возникает потребность в пристальном изучении данного процесса. Таким образом, требуется процесс разделения профилей для получения четких полос частот, которые лучше отражают вариации данного процесса или функцию компонента, который намереваются получить. Одним из последних достижений в данной области является использование вейвлетов для анализа текстуры поверхности.
      Вейвлет является перспективным инструментом для анализа текстуры поверхности, так как он может разлагать любую поверхность (дву-, трехмерную) на многошкальное отображение. В то время, как вейвлеты широко позиционируются как имеющие характеристики и возможности, превосходящие традиционные фильтры, основополагающие понятия, такие как выбор вейвлетных базисов, остались нерассмотренными.
      Основная задача данной работы – показать различия между вейвлетами в элементах характеристик передаваемых данных сопряженных с ними блоков фильтров, что присуще анализу поверхности.

      Из теории Фурье хорошо известно, что сигнал может быть представлен как сумма последовательностей синусов и косинусов. Тем не менее, синусы и косинусы, составляющие основу метода Фурье, являются нелокальными функциями, которые имеют только частотное разрешение и не имеют временного разрешения. Это означает, что хотя преобразование и может быть способно определять все частоты, присутствующие в сигнале, оно не может показать когда или где они присутствуют. Принцип неопределенности Гейзенберга гласит, что умножение временной вариации и частотной вариации базисной функции на стандартную единицу всегда будет больше половины. Следовательно, существует зависимость между временной (пространственной в поверхностном анализе) локализацией и частотной локализацией базиса. Локализация подразумевает, что базисная функция имеет не-нулевое значение в конечном интервале. По крайней мере синусоидальный сигнал имеет бесконечно большую поддержку (без локализации) во временном интервале и нулевую поддержку по длине (одна определенная частота) в частотном интервале. Вейвлеты преодолевают отсутствие синусоид и импульсов, имея локализацию как во временном (пространственном) так и в частотном интервале, чтобы получить разрешение в обоих интервалах.

       В вейвлет-анализе сигнал преобразуется в ряд, использующий семейство вейвлет-базисов. Крупные базисы представляют собой низкочастотные компоненты, а небольшие базисы представляют высокочастотные компоненты. Конечным результатом является совокупность частотно- временных отображений сигнала с различными разрешениями и в основном упоминается как отображение, имеющее множественное решение. Анализ множественных решений стал возможным благодаря открытиям Маллата и Мейера, которые показали равенство между пирамидальным алгоритмом, используемым в дискретных двухканальных фильтрах и двухэлементной вейвлетной трансформации (дискретная вейвлетная трансформация с двухэлементной шкалой). В то время как пирамидальный алгоритм дает возможность быстрого применения анализа множественных решений вейвлет-теория подводит под это прочную математическую базу.

      Данный раздел вкратце обращается к математической теории, необходимой для вейвлет-анализа. Маллат и Стренг провели всесторонний обзор теории вейвлетов и фильтрующих блоков. Здесь представлен сжатый обзор. Цель вейвлет-анализа – разложить данный сигнал на серию вейвлетов, которая создана из материнского вейвлета путем расширения и преобразования. Материнский вейвлет – это интегрируемая квадратичная функция ψ(x) с нулевым средним значением, например:

(1)

(2)

      Семейство вейвлетов получается путем установления зависимости ψ(x) от S и преобразования ее при помощи t, коэффициент s^1/2 iслужит для нормализации энергии по различным шкалам:

(3)

      Вейвлет-преобразования функции f(x)в позиции t и по шкале s – это

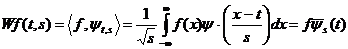(4)

      с

(5)

      Преобразование Фурье

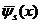
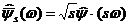(6)

      Из-за того, что

      Вейвлет работает как полосовой фильтр. Масштаб s rотображает зависимость между пространственным и частотным разрешением. Так как масштаб возрастает, пространственное разрешение снижается, а частотное разрешение возрастает в соответствии с принципом неопределенности Гейзенберга. Сигнал может быть воссоздан обратным вейвлет-преобразованием, как следует из формулы:

(7)

      Где C_ψ рассчитывается как:

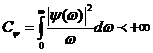(8)

      В то время, как Wf(t,s) лишь подсчитывается на малых масштабах s<s₀, таких, как высокочастотные детали, чтобы воссоздать f(x) необходима такая дополнительная информация, на больших масштабах s>s₀ аппроксимация низкой частоты. Это достигается введением скейлинг-функции ф, то есть объединение вейвлетов в таких масштабах больше, чемs₀=1. Коэффициент его Фурье преобразования определяется как:

(9)

      Из равенства (9):

(10)

      Таким образом скейлинг-функция может быть передана как импульсный ответ фильтра нижних частот, выраженный

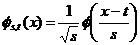
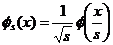
      и

      Тогда низкочастотная аппроксимация f по шкале s :

(11)

      Таким образом равенство (7) может быть переписано, как:

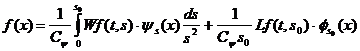(12)

      Функция может быть преобразована как сумма аппроксимации на определенной шкале масштабирования и детали на меньших шкалах масштабирования. Преобразование, описанное выше – это непрерывное вейвлет-преобразование (НВП), которое служит математической основой всем практическим применениям вейвлета. Детали НВП объяснены Добеши и Маллатом.