Левчик Дмитрий Валентинович

Факультет инженерной механики и машиностроения

Специальность: подъемно-транспортные, строительно-дорожные, мелиоративные машины и оборудование

Автореферат по теме дипломной работы:

ИССЛЕДОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ КЛЕЕВОГО СТЫКА КОНВЕЙЕРНОЙ ЛЕНТЫ С ПРИМЕНЕНИЕМ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ

ВВЕДЕНИЕ

Подземный транспорт остаётся одним из проблемных вопросов угольной отрасли, крупные шахты, оснащённые высокопроизводительными добывающими комплексами с суточной нагрузкой на лаву 1000 т угля и более, должны иметь развитый конвейерный транспорт, обеспечивающий выдачу топлива на поверхность, а колёсный – выполнять вспомогательную функцию по доставке людей, оборудования и материалов. Большое значение в работе подземного транспорта приобретают надёжность, эффективность его использования, расходы оборудования, материалов, электроэнергии, а также трудозатраты. Лента является основным и наиболее дорогим, но наименее долговечным элементом ленточного конвейера. Стоимость ее составляет около половины общей стоимости конвейерной установки, а высокие амортизационные отчисления на ленту являются немаловажным фактором, определяющим область применения и экономическую эффективность конвейерного транспорта. Поэтому правильный выбор конструкции и характеристик ленты наряду с обеспечением надлежащих условий ее эксплуатации, с чем связано удлинение сроков службы ленты, имеет существенное значение.

Обзор литературы

Научные основы теории совершенствования конструкций и методов расчета стыковки резинотканевых лент конвейеров посвящены исследования проф., д.т.н. В.Г. Дмитриева, проф., д.т.н. И.Г. Штокмана, проф., к.т.н. Е.М. Высочина, проф., к.т.н. Д.Ш. Монастырского, к.т.н. В.И. Кузьменко, к.т.н. Ю.И. Григорьева, к.т.н. Е.Х. Завгороднего, к.т.н. В.Т. Полунина, к.т.н. В.Н. Григорьева и многих других ученых, как в нашей стране, так и за рубежом. Данным вопросом занимаются такие организации как: Санкт-Петербургский Государственный Университет, Запорожский национальный технический университет, Донецкий национальный технический университет, ООО «Горный институт» города Днепропетровск, ВНИИПТМАШ и т.д.

Цель и задачи работы

Цель работы: провести анализ влияния параметров стыкового клеевого соединения на его напряженно деформированное состояние, используя моделирование в программной среде SolidWorks 2004 с интегрированным расчетным модулем CosmosWorks 2004 с применением метода планирования эксперимента, что позволит обосновать длину нахлеста, снизив при этом затраты на изготовление стыка.

Задачи:

• проанализировать методы используемые в холодной вулканизации стыков конвейерной ленты;
• применить современное программное обеспечение для расчетов модели клеевого стыка конвейерной ленты;
• построить графики зависимостей внутренних напряжений от свойств клеевого слоя;
• составить расширенные матрицы планов экспериментов;
• применить метод расчета элементарных конструкций композиционных материалов к исследуемой модели;

Прогнозируемые результаты работы

Данная работа направлена на изучение факторов, влияющих на прочность стыкового соединения. Планируется получить зависимости, и математическую модель напряженно-деформированного состояния стыкового соединения конвейерной ленты. Получить детальный анализ факторов взаимодействия клеевого слоя с тканевой прокладкой стыка.

Построение физической модели исследуемого образца

Современные компьютерные технологии позволяют нам все проще моделировать и рассчитывать разные механические системы. Для реализации этого существует довольно таки большое количество программных сред работающих в том или ином направлении. В данной работе была выбрана программа для построения 3D модели и проведения расчета на прочность – SolidWorks 2004 с встроенным расчетным модулем CosmosWorks 2004.

Построение физической модели включает в себя идеализацию свойств конструкции и внешних воздействий. В общем случае конструкция, изготовленная из реального материала, находящаяся под действием внешних нагрузок, может иметь много особенностей, включающих в себя несовершенство формы, несплошность и неоднородность свойств материала, особенности в характере внешнего нагружения и т.п. В практических расчетах учесть все имеющиеся особенности конструкции, материала и нагружения невозможно. Конечно, привлечение ЭВМ расширило возможности учета в прочностных расчетах некоторых из перечисленных выше особенностей, но необходимо понимать, что как бы ни были велики мощности современных ЭВМ, их быстродействие и объем памяти, но и они не безграничны. Поэтому, приступая к практическим расчетам, мы вынуждены подменять реальные тела некоторыми идеализированными объектами - «механическими моделями».

Реальное тело, представляющее резинотканевую ленту, можно рассмотреть как бесконечную систему материальных точек, определенным образом взаимодействующих между собой. С точки зрения атомного строения вещества и существования сил межатомного взаимодействия каждой из материальных точек свойственна определенная индивидуальность. Однако проследить за состоянием каждой из материальных точек совершенно невозможно, поэтому приходится вводить некоторые осредненные характеристики, описывающие взаимодействие между атомами, отказавшись от рассмотрения каждого атома в отдельности (статистическая физика). Для описания поведения тела сведения об их атомной структуре не нужны. Реальное тело заменяется воображаемой (модельной) сплошной средой. Среда называется сплошной, если любой объем, выделенный из нее, содержит вещество. Такое представление о сплошной среде противоречит представлению об атомном строении вещества, однако оно чрезвычайно упрощает математическое описание поведения твердых тел под действием приложенной нагрузки.

Еще одной идеализацией реального тела является присвоение ему свойств однородности. Среда называется однородной, если свойства выделенных из нее малых объемов одинаковы. Естественно, здесь речь идет о тех свойствах, которые определяются посредством механического эксперимента. Определенной идеализации подвергается также и понятие «внешние силы». В механике предполагается, что сила полностью определена, если задан соответствующий вектор, при этом сила рассматривается как результат взаимодействия двух твердых тел. С этой точки зрения вектор силы, действующей на поверхность тела, означает сосредоточенную силу, т.е. силу, приложенную в точке. Однако, в действительности, «сосредоточенных» сил не существует.

Рисунок 1 – Габаритные размеры модели исследуемого образца

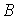- ширина стыкуемых элементов,

- длина тканевой прокладки,

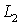- длина клеевого слоя,

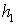- толщина клеевого слоя,

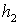- толщина тканевой прокладки.

Значения параметров исследуемой модели: , , , , .

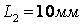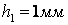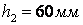Разбиение 3D модели исследуемого образца на конечные элементы

Основная идея метода конечных элементов состоит в том, что любую непрерывную величину (перемещение, температура, давление и т.п.) можно аппроксимировать моделью, состоящей из отдельных элементов (участков). На каждом из этих элементов исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, которая строится на значениях исследуемой непрерывной величины в конечном числе точек рассматриваемого элемента (рис. 2).

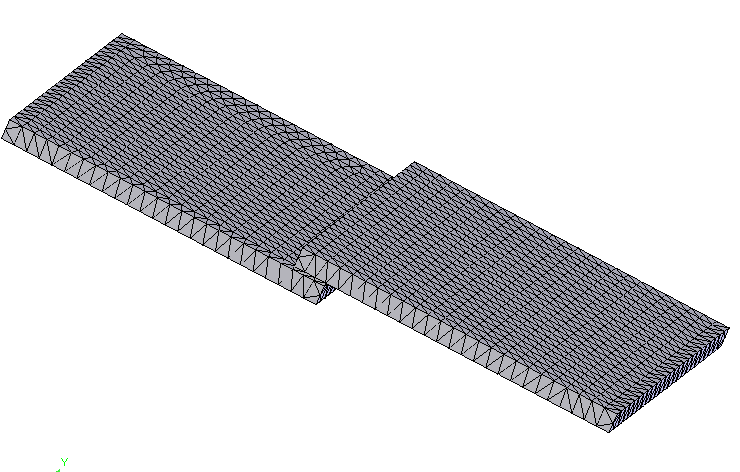
Рисунок 2 – Применение МКЭ к рассматриваемой модели

Приложение силы ограничений к исследуемой модели

Исследуемая модель имеет следующие граничные условия и приложенные силы: зафиксирована одним торцом тканевой прокладки (имитирующая жесткое закрепление в разрывной машине), а с другой стороны приложена распределенная нагрузка по всей поверхности торца (рис. 3).

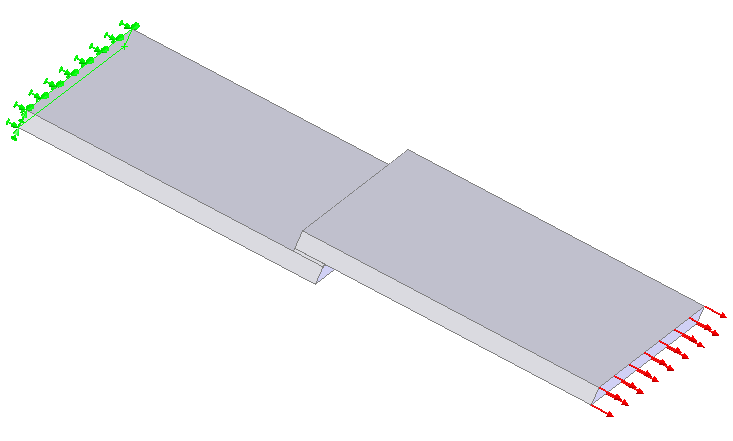
Рисунок 3 – Схема приложения сил и граничных условий к исследуемому образцу

Представление результатов расчета

Результаты расчета по численным моделям радикально отличаются от результатов аналитических вычислений. Величина и способ интерпретации последних, как правило, однозначны. Численные же методы для приблизительно поставленной задачи, решенной непрямыми алгоритмами, дают оценку, которая может быть весьма неоднозначно истолкована. А следовательно, интерпретация результатов применения алгоритмов типа МКЭ – занятие неформальное, требующее определенного понимания существа явления.

На основе расчетов нами были получена эпюра напряженно деформированного состояния клеевого стыка резинотканевой конвейерной ленты, представленная на рисунке 4. В ней представлены внутренние напряжения в каждом из узлов элементов. Результаты отображаются с помощью цветовой палитры: синий цвет указывает на минимальное значения напряжений, а красный – на максимальные.

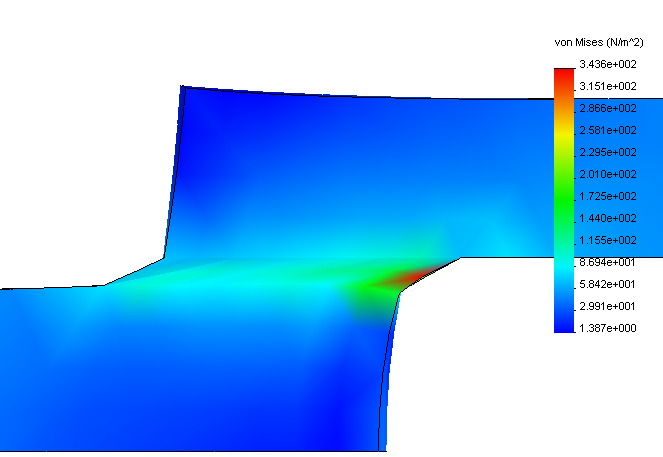
Рисунок 4 – Эпюра внутренних напряжений в исследуемом образце

Анализируя эпюру приведенную на рисунке 4 следует, что критические напряжения, которые могут привести к разрушению, находятся в середине клеевого слоя.

ИССЛЕДОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЭЛЕМЕНТАРНОГО ВЗАИМОДЕЙСТВИЯ В СИСТЕМЕ «ПРОКЛАДКА – КЛЕЕВОЙ СЛОЙ – ПРОКЛАДКА»

Для исследования элементарной системы «тканевая прокладка – клеевой слой – тканевая прокладка» был применен метод планирования эксперимента. Данный способ обработки данных позволяет повысить производительность труда и надежность полученных результатов. Так как данный эксперимент многофакторный и связан с отысканием оптимальных условий нами был применен метод полного факторного эксперимента типа 2^k, что позволит достаточно полно изучить поведение системы в значительном числе экспериментов.

Локальную область определения факторов установим из априорных соображений. В ходе эксперимента факторы варьировались на двух уровнях. Интервалы варьирования, а так же их значения на основном, верхнем и нижнем уровнях приведены в таблице 1. Основной уровень является исходной точкой для построения плана эксперимента, а интервалы варьирования определяют расстояния до него по осям координат от верхнего и нижнего уровней.

Таблица 1 – Уровни факторов

Факторы	P, Н/м^2	V	E, МПа	L2, мм	h1, мм
Основной уровень (Xio)	125	0,4925	6,55	15	1,5
Интервал варьирования (deltaXi)	25	0,0025	0,45	5	0,5
Верхний уровень (Хi = +1)	150	0,495	7	20	2
Нижний уровень (Хi = -1)	100	0,49	6,1	10	1

Число опытов в нашем случае составит:

N = 2^5 = 32

Кодированный и натуральные значения факторов найдем используя формулы и занесем в таблицу 2.

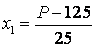
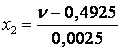
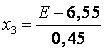
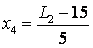
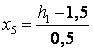
Результатом являются значения факторов, равные +1 (верхний уровень) и –1 (нижний уровень).

Таблица 2 – Матрица плана эксперимента.

Уравнение регрессии для k=5 имеет вид:

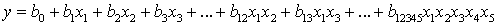
Линейные коэффициенты регрессии рассчитываются по формуле:

Коэффициент регрессии, характеризующий парное взаимодействие факторов, находят по формуле:

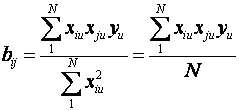
Составление математической модели в относительных единицах

Используя полученные значения, на основании уравнения регрессии составим математическую модель:

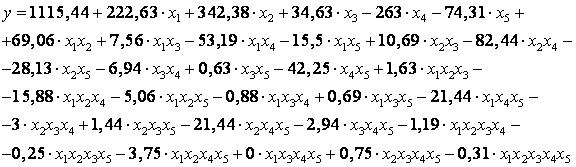
Наименьшие значения функции удалось достичь при нижнем уровне P, V и Е и верхнем уровне L2 и h1. Т.е. самое прочное соединение при функции

Влияния исследуемых факторов на критические напряжения в клеевом соединении

Для построения графиков, описывающих влияние исследуемых факторов на внутренние напряжения в клеевом стыке резинотканевой ленты, исходя из крайних значений границ факторов были получены процентные показатели максимального и минимального изменения факторов по отношению к нулевому уровню. Значение внутренних напряжений на этих границах по отношению к значению в нулевой точке показывает на сколько данный фактор влияет на параметр оптимизации в соединении.

Рисунок 5 – Влияние исследуемых факторов на критические напряжения

Рисунок 6 – Влияние исследуемых факторов на степень изменения параметра оптимизации

Исходя из полученных данных на рисунках 5 и 6 сделаем следующие выводы:

• Наибольшее влияние на максимальное значение внутренних напряжений оказывает коэффициент Пуассона. При изменении этого параметра на 0,5% значения параметра оптимизации изменяются на 30%.
• Наименьшее влияние в исследуемых пределах оказало высота клеевой пленки.
• Фактор распределенной нагрузки оказал на модель линейное влияние – при увеличении его на 20%, внутренние напряжения также увеличиваются на 20%.
• Модуль Юнга значительно не повлиял на исследуемую модель.
• Длина клеевой пленки L2 существенно влияет на параметр оптимизации. При увеличении длины на 1/3 прочность стыка увеличивается на 23,6%.

ИССЛЕДОВАНИЕ ВЛИЯНИЯ УГЛА СКОСА СТЫКА РЕЗИНОТКАНЕВОЙ КОНВЕЙЕРНОЙ ЛЕНТЫ НА ЕГО НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ

Резервом повышения прочности стыка является косой срез его ступеней по отношению к продольной оси ленты под углом alfa. При этом напряжения в каркасе ленты и в резиновых прослойках распределяется на большую длину и их абсолютная величина снижается. Опыт эксплуатации показывает, что при косом срезе ступеней улучшаются условия входа стыка на барабаны и ролики конвейера, значительно повышается надежность соединений, что особенно заметно при эксплуатации дорогостоящих, высокопрочных лент на конвейерных линиях большой протяженности и производительности.

Исследование влияния угла скоса на НДС стыка ленты

С помощью методов, изложенных выше, проведем моделирование деталей стыков лент, с различным углом скоса. Затем проанализируем их напряженно деформированное состояние в клеевом слое.

Исследуемый диапазон углов скоса – от 0° до 45°. Исследуем напряженно-деформируемое состояние клеевого слоя при разных растягивающих силах.

Это будет выглядеть следующим образом:

Рисунок 7 – Модель стыка ленты при угле скоса 0° (45°)

Таблица 4 – Внутренние напряжения в клеевом слое.

Динамику изменения внутреннего напряжения в стыке конвейерной ленты, в зависимости от угла скоса можно увидеть на Рисунке 8.

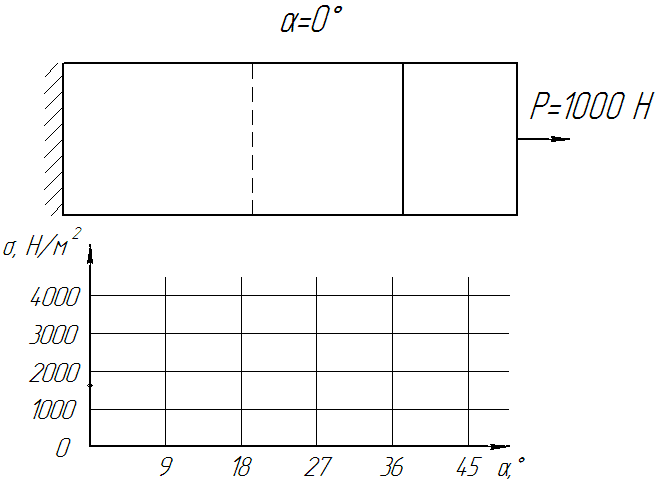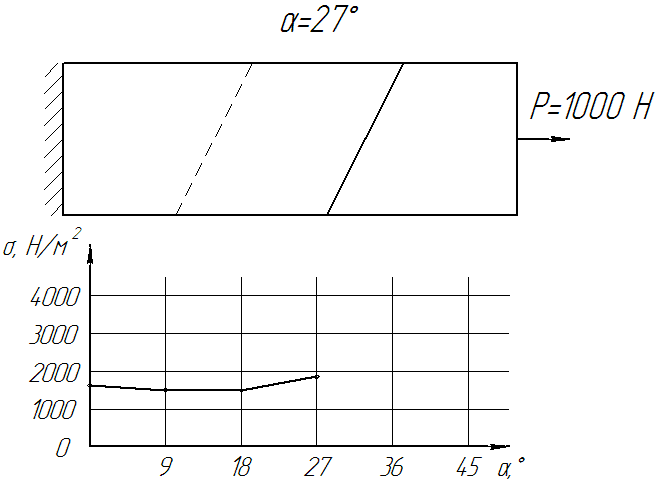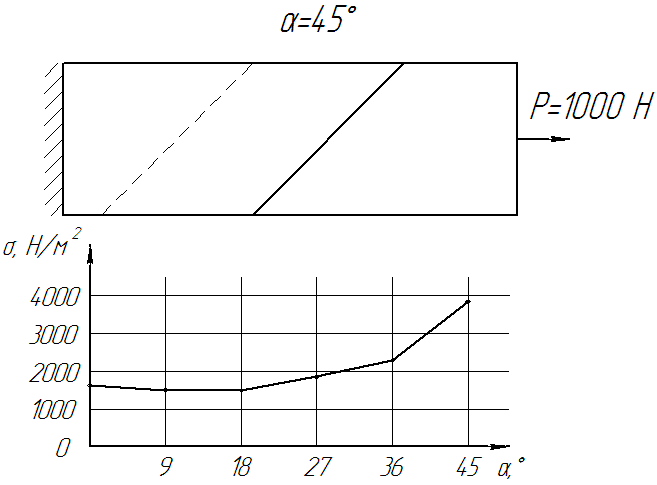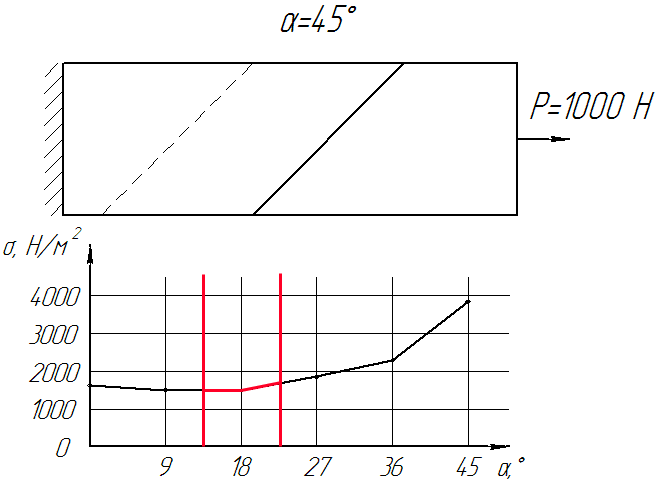
Рисунок 8. - Динамика изменения напряжения от угла скоса стыка (Кол-во кадров: 12, кол-во циклов: бесконечное, задержка: 75 мс, размер файла: 92,2 КБ)

По полученным данным построим графики напряженно деформированного состояния клеевого стыка ленты.

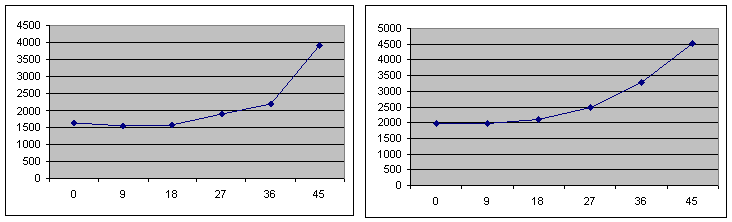
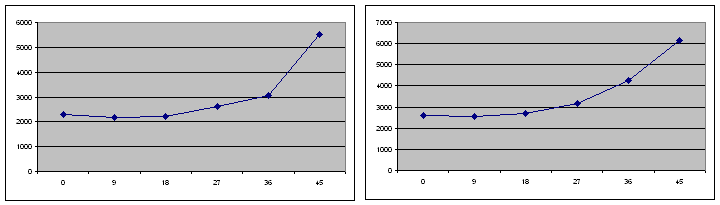
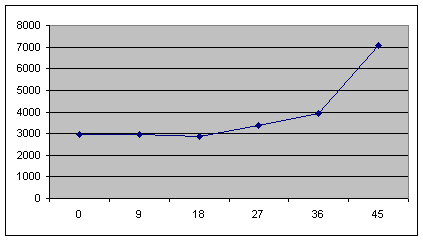
Рисунок 9. – Графики распределения напряжения при 1000, 1200, 1400, 1600, 1800 Н

Из полученных графиков следует четкая зависимость распределения напряженно-деформированного состояния клеевого слоя стыка в зависимости от угла скоса стыка. Примерно до угла 20° наблюдается практически прямолинейный рост напряженно деформированного состояния внутри клеевого стыка ленты, а затем значительный его рост. Самый оптимальный угол скоса (по НДС) находится в пределах от 12° до 20°.

При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2010. Полный текст работы по теме могут быть получены у автора или его научного руководителя после указанной даты.

Литература

1. Высочин Е.М. Стыковка и ремонт конвейерных лент на предприятиях черной металлургии/ Е.М. Высочин, Е.Х. Завгородний, В.И. Заренков. - М.: Металлургия, 1989, с. 192.
2. Билан И.Е. О прочности связи между слоями резинотканевых конвейерных лент – В кн. Вопросы рудничного транспорта, в.9./ И.Е. Билан. - М.: «Недра». 1965 – с. 54-62.
3. Билан И.Е. Макро- и микроисследования конвейерных лент. – В кн.: Вопросы рудничного транспорта, в.8/ И.Е. Билан. - М.: «Недра», 1965 – с. 23-37.
4. Монастырский Д.Ш. Об изменении прочности связи между прокладками резинотканевых конвейерных лент по толщине. – В кн.: Вопросы рудничного транспорта, в.12/ Д.Ш. Монастырский. - М.: «Недра», 1972 – с. 60-69.
5. Алямовский А.А. SolidWorks/CosmosWorks. Инженерный анализ методом конечных элементов/ А.А. Алямовский. – М.: ДМК Пресс, 2004. – 432 с.: ил.
6. Агапов В.П. «Метод конечных элементов в статике, динамике и устойчивости пространственных тонкостенных подкрепленных конструкций». учебное пособие/ В.П. Агапов. - М.: изд. АСВ, 2000, 152 стр., с илл.
7. Хамханов К.М. Методическое пособие: Основы планирования эксперимента/ К.М. Хамханов. - Улан-Уде, 2001.
8. Якушев В. Л. Применение 3D-конечных элементов для расчета тонкостенных конструкций: [Электронный ресурс]. - Режим доступа: http://www.ipdn.ru/rics/vk/1VK-yak.pdf
9. Шимановский А. О. «Применение метода конечных элементов в решении задач прикладной механики: [Электронный ресурс]. - Режим доступа: http://www.belsut.gomel.by/Ellibrary/1/70.pdf

© 2010 Левчик Д.В.