|
ABSTRACT of the qualification master’s work
RESEARCH OF THE TENSELY-DEFORMED STATE OF GLUE JOINT OF CONVEYER BELT WITH THE USE OF METHOD OF EVENTUAL ELEMENTS
INTRODUCTION
Underground transport is one of the problematic issues coal industries, large mines are equipped with high-producing complexes with a daily load of lava at 1000 tons of coal and more should be developed pipeline transportation, provides delivery of fuel to the surface, and wheels - has a supporting role for the delivery people, equipment and materials. Of great importance in the underground transport is reliability, efficiency of its use, the cost of equipment, materials, electricity and labor costs. The Ribbon is the main and most expensive, but least durable part of a conveyor belt. The cost is about half of its total cost of pipeline installation, and high depreciation charges on the tape is an important factor in determining the scope and cost-effectiveness of conveyor transport. Therefore the correct choice of design and characteristics of tape along with the provision of appropriate conditions for its operation, with associated lengthening the service life of belts, is essential.
Literature Review
Improved docking conveyor belts engaged prof., d.t.n. V.G. Dmitriev, prof., d.t.n. I.G. Shtockman, prof., d.t.n. E.M. Vysochina, prof., d.t.n. D.Sh. The Monastirsky, d.t.n. V.I. Kuzmenko, d.t.n. Y.I. Grigoriev, and many other scientists. These issues are engaged in such organizations as the St. Petersburg State University, Zaporozhye National Technical University, Donetsk National Technical University and others.
The purpose and objectives
The purpose: analyze the effect of the parameters of a butt adhesive joint at its stress-strain state, using the simulation software environment of SolidWorks 2004 with integrated calculation module CosmosWorks 2004.
Objectives:
- Review the methods used in the cold vulcanization of conveyor belt joints;
- Use advanced software to model calculations of adhesive joints of conveyor belts;
- Plotted as a function of internal stresses on the properties of the adhesive layer;
- Build advanced matrix of experiments;
- Apply the method of calculating the basic structures of composite materials to study the model;
Projected results of the work
This work aims to study factors affecting the strength of a glue joint. Planned to obtain the dependence, and the mathematical model of the stress-strain state of a joint weld conveyor belt. Get a detailed analysis of interactions with the adhesive layer of tissue lining the joint.
Construction of a physical model of the sample
Construction of a physical model includes the idealization of the properties of the structure and external influences. In general, the design is made of real material, which is under the influence of external loads, may have a lot of features that include the imperfections of form, lack of adhesion and heterogeneity of material properties, especially in the nature of external loading.
The real body represents the rubber strip can be considered as an infinite system of material points in a certain way of interacting with each other. From the viewpoint of the atomic structure of matter and the existence of interatomic forces of each material point characterized by a certain personality.
Another idealization of the real body is the assignment of the properties of homogeneity. A medium is called homogeneous if the properties extracted from her small amounts of the same.
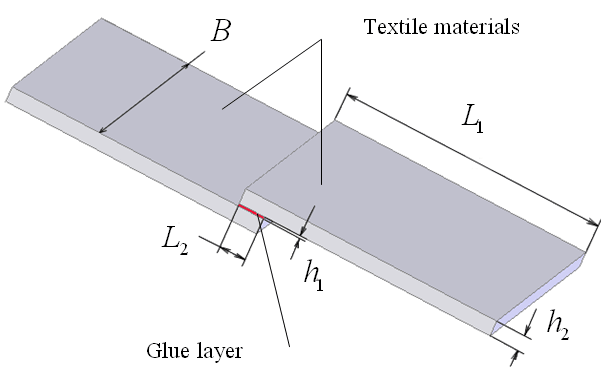
Figure 1 - Dimensions of the model sample
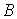- The width of the stackable elements,
- the length of the tissue lining,
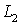- the length of the adhesive layer,
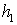- the thickness of the adhesive layer,
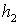- the thickness of the tissue lining.
The parameters of the model: 
, 
, 
, 
, 
.
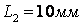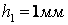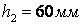Partitioning of 3D model of the sample into finite elements
The main idea of the finite element method consists in the fact that any continuous quantity (displacement, temperature, pressure, etc.) can be approximated by a model consisting of individual elements (sections). At each of these elements investigated continuous quantity is approximated by a piecewise continuous function, which is based on the values of the studied continuous variables in a finite number of points of the element.
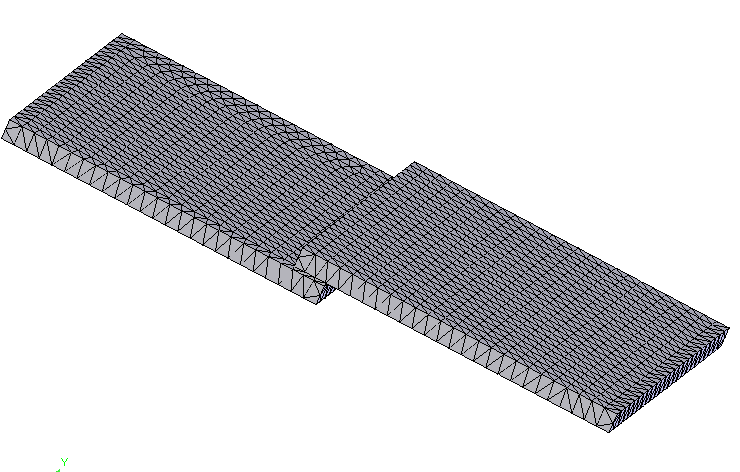
Figure 2 - Application of MFE to the model
The tested model has the following boundary conditions and applied forces: one fixed face of the tissue lining (simulating rigid fastening to the testing machine), and the other parties to make the distributed load over the entire surface end.
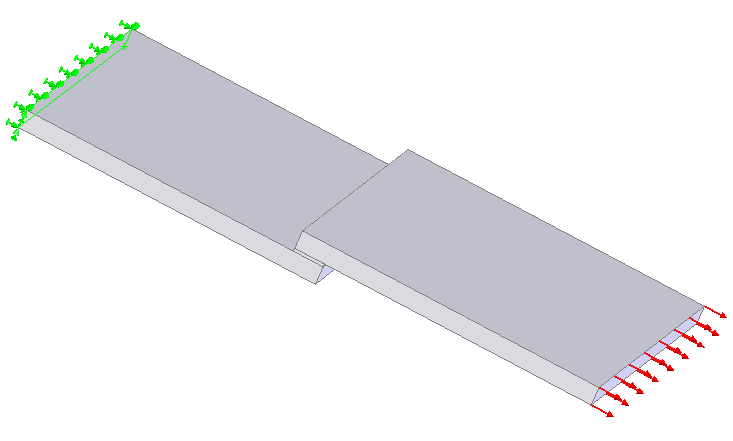
Figure 3 - Scheme of application of forces and boundary conditions for the test sample
Presentation of results of calculation
The results of the calculation of the numerical models are radically different from the results of analytical calculations. Based on the calculations we have obtained the stress diagram strained state of glue joints rubber-belt.
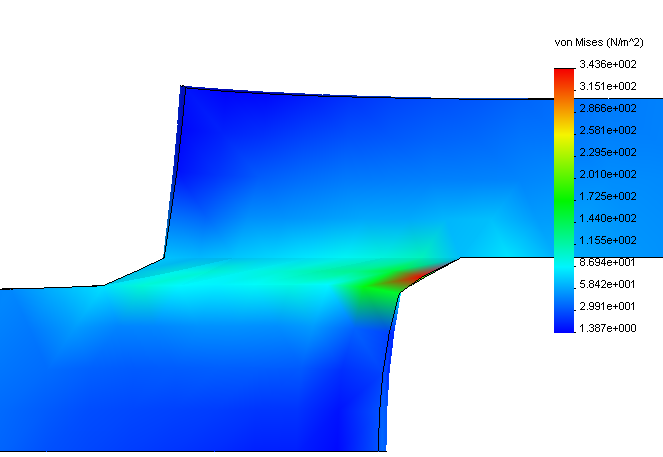
Figure 4 - Variation of internal stress in the sample
Analyzing the diagram, Figure 4 shows that the critical stress, which can lead to destruction, are in the middle of the adhesive layer.
INVESTIGATION OF STRESS-STRAIN STATE OF ELEMENTARY INTERACTIONS IN THE SYSTEM "PADS - GUM - LAYING"
Local area to determine the factors set out a priori considerations. In the experiment, the factors were varied at two levels. The ranges of variation, as well as their significance in the main, upper and lower levels are given in Table 1.
Table 1 - Levels of factors
| Factors | P, Н/м^2 | V | E, МПа | L2, мм | h1, мм |
| Basic level (Xio) | 125 | 0,4925 | 6,55 | 15 | 1,5 |
| The range of variation (deltaXi) | 25 | 0,0025 | 0,45 | 5 | 0,5 |
| Upper level (Хi = +1) | 150 | 0,495 | 7 | 20 | 2 |
| Lower level (Хi = -1) | 100 | 0,49 | 6,1 | 10 | 1 |
Number of experiments in our case is:
Coded and natural values of the factors we find using the formula
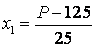
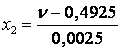
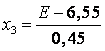
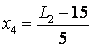
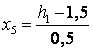
Table 2 - Matrix plan experiment.
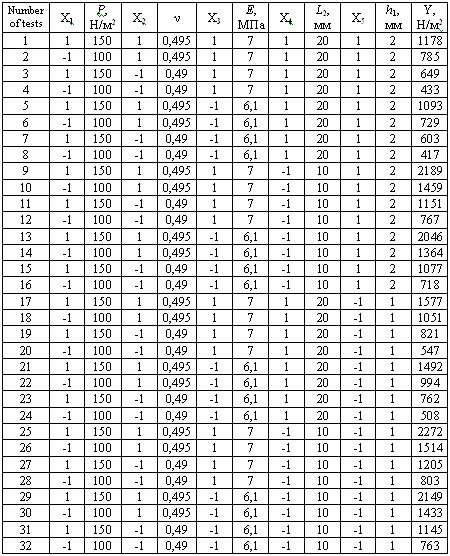
The regression equation for k = 5 has the form:
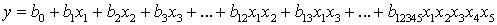
Linear regression coefficients calculated by the formula:
Regression coefficients, characterizing the pair interactions of the factors found by the formula:
A mathematical model in relative units
Using the values obtained on the basis of regression equation form the mathematical model:
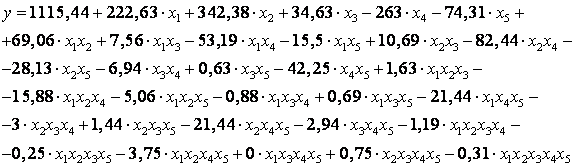
The lowest values of the function has been achieved at the lower level of P, V and E and the upper level L2 and h1. Very strong connection with the functions
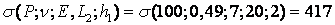
The effects of the investigated factors on the critical stresses in the adhesive compound
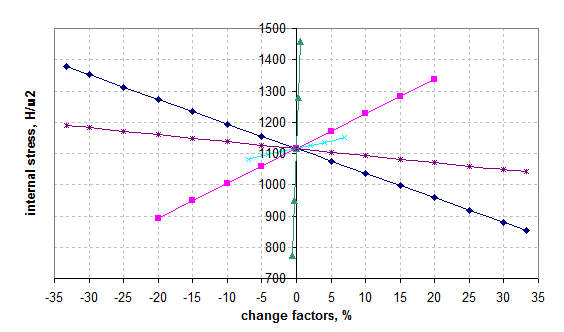
Figure 5 - Effect of studied factors on the critical stress
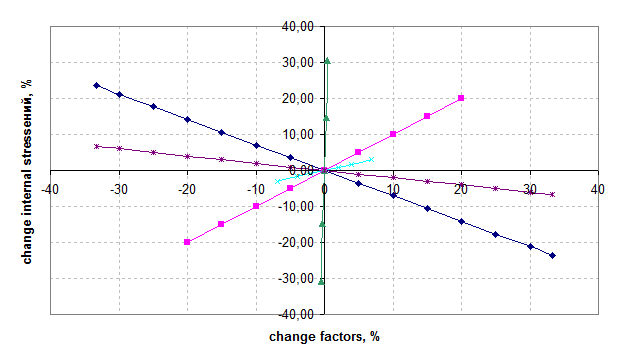
Figure 6 - Effect of studied factors on the degree of change in the parameter optimization
Based on the data obtained in Figures 5 and 6 the following conclusions:
- The greatest influence on the maximum value of internal stress has a Poisson's ratio. When you change this setting on 0,5% optimization settings are changed to 30%.
- The smallest influence in the study had a height within the adhesive film.
- Distributed load factor had on the model of a linear effect - by increasing it by 20%, internal stresses are also increased by 20%.
- Young's modulus was not significantly affected the investigated model.
- The length of the adhesive film L2 significantly affect the parameter optimization. With an increase in length by 1 / 3 the strength of the joint increased by 23,6%.
RESERCH ON JOINT ANGLE SCOSA RUBBER CONVEYOR BELT TO THE ITS STRESS-STRAIN STATE
The investigated range of angles of bevel - from 0 ° to 45 °. We investigate the stress-deformed state of the adhesive layer with different tensile strength.
The dynamics of changes in the internal stresses in the junction of the conveyor belt, depending on the angle of bevel can be seen in Figure 7.
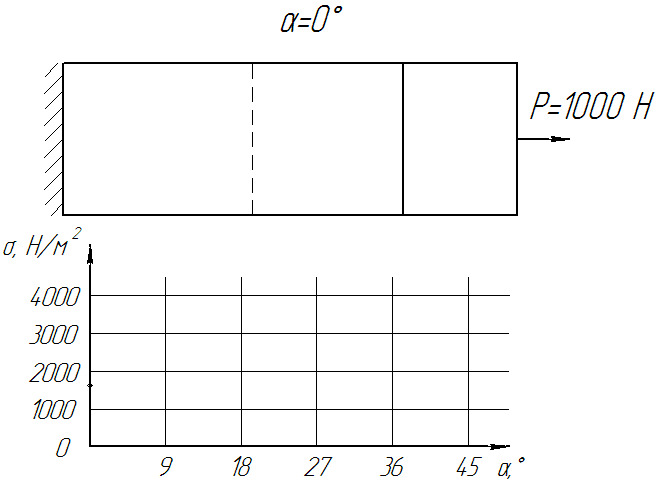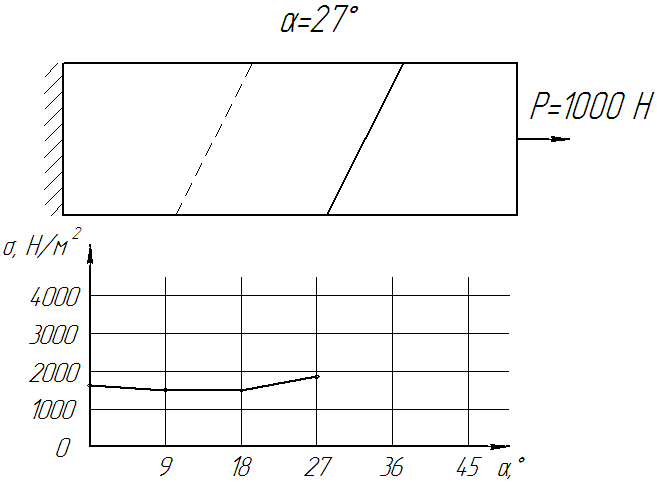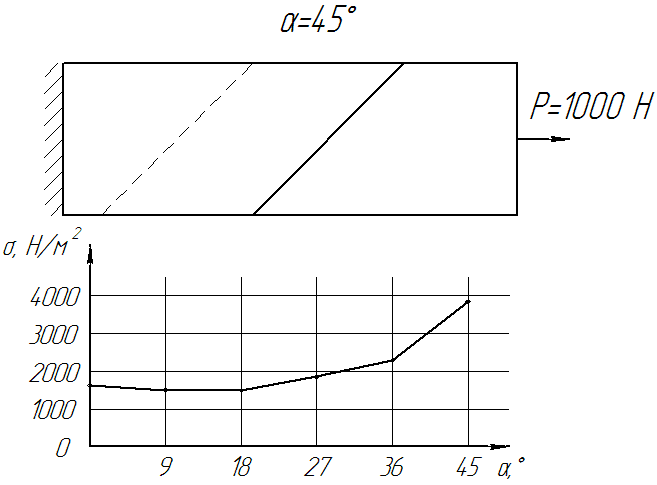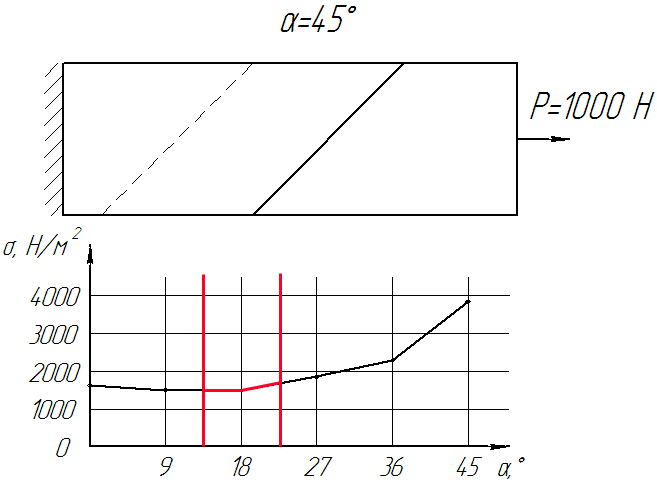
Figure 7. - Dynamics of change of voltage on the angle of bevel joint (Number of frames: 12, number of cycles: the infinite, delay: 75 ms, file size: 92,2 KB)
According to our data we construct graphs of stress strain state of adhesive joint tape.
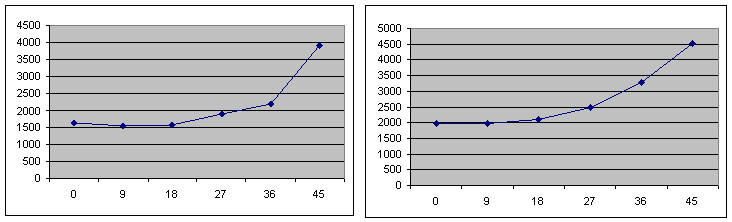
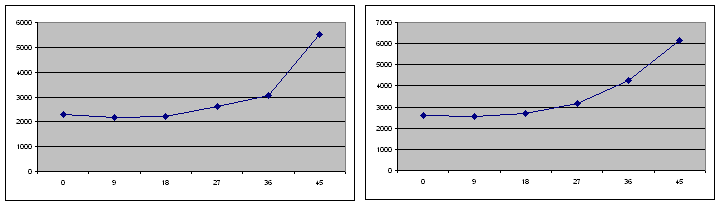
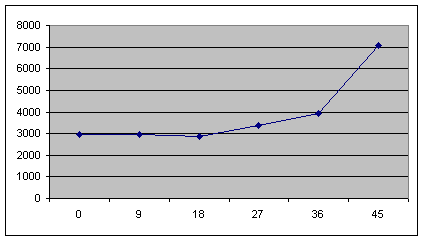
Figure 8. - Charts voltage distribution in 1000 (a), 1200 (b), 1400 (c), 1600 (d), 1800 (e) H
From these graphs should be a clear correlation distribution of the stress-strain state of the adhesive layer interface depending on the angle of bevel joint. Up to about 20 ° there is practically a straight increase in the stress strain state within the adhesive joint tape, and then its significant growth. The most optimal canting angle (VAT) is within from 12 ° to 20 °.
Sourses
- Высочин Е.М. Стыковка и ремонт конвейерных лент на предприятиях черной металлургии/ Е.М. Высочин, Е.Х. Завгородний, В.И. Заренков. - М.: Металлургия, 1989, с. 192.
- Билан И.Е. О прочности связи между слоями резинотканевых конвейерных лент – В кн. Вопросы рудничного транспорта, в.9./ И.Е. Билан. - М.: «Недра». 1965 – с. 54-62.
- Билан И.Е. Макро- и микроисследования конвейерных лент. – В кн.: Вопросы рудничного транспорта, в.8/ И.Е. Билан. - М.: «Недра», 1965 – с. 23-37.
- Монастырский Д.Ш. Об изменении прочности связи между прокладками резинотканевых конвейерных лент по толщине. – В кн.: Вопросы рудничного транспорта, в.12/ Д.Ш. Монастырский. - М.: «Недра», 1972 – с. 60-69.
- Алямовский А.А. SolidWorks/CosmosWorks. Инженерный анализ методом конечных элементов/ А.А. Алямовский. – М.: ДМК Пресс, 2004. – 432 с.: ил.
- Агапов В.П. «Метод конечных элементов в статике, динамике и устойчивости пространственных тонкостенных подкрепленных конструкций». учебное пособие/ В.П. Агапов. - М.: изд. АСВ, 2000, 152 стр., с илл.
- Хамханов К.М. Методическое пособие: Основы планирования эксперимента/ К.М. Хамханов. - Улан-Уде, 2001.
- Якушев В. Л. Применение 3D-конечных элементов для расчета тонкостенных конструкций: [Electronic resource]. - Access mode: http://www.ipdn.ru/rics/vk/1VK-yak.pdf
- Шимановский А. О. «Применение метода конечных элементов в решении задач прикладной механики: [Electronic resource]. - Access mode: http://www.belsut.gomel.by/Ellibrary/1/70.pdf