| 
Автореферат
ДОСЛІДЖЕННЯ НАПРУЖЕНО-ДЕФОРМОВАНОГО СТАНУ КЛЕЙОВОГО СТИКУ КОНВЕЄРНОЇ СТРІЧКИ ІЗ ЗАСТОСУВАННЯМ МЕТОДУ КІНЦЕВИХ ЕЛЕМЕНТІВ
ВСТУП
Підземний транспорт залишається одним з проблемних питань вугільної галузі, великі шахти, оснащені високопродуктивними видобувними комплексами з добовою навантаженням на лаву 1000 т вугілля і більше, повинні мати розвинений конвеєрний транспорт, який забезпечує видачу палива на поверхню, а колісний - виконувати допоміжну функцію з доставки людей, обладнання та матеріалів. Велике значення у роботі підземного транспорту набувають надійність, ефективність його використання, витрати обладнання, матеріалів, електроенергії, а також трудовитрати. Стрічка є основним і найбільш дорогим, але найменш довговічним елементом стрічкового конвеєра. Вартість її становить близько половини загальної вартості конвеєрної установки, а високі амортизаційні відрахування на стрічку є досить важливим фактором, що визначає область застосування і економічну ефективність конвеєрного транспорту. Тому правильний вибір конструкції і характеристик стрічки разом із забезпеченням належних умов її експлуатації, з чим пов'язано подовження термінів служби стрічки, має істотне значення.
Огляд літератури
Наукові основи теорії удосконалення конструкцій і методів розрахунку стиковки гумотканинних стрічок конвеєрів присвячені дослідження проф., д.т.н. В.Г. Дмитрієва, проф., д.т.н. І.Г. Штокмана, проф., К.т.н. Є.М. Височина, проф., к.т.н. Д.Ш. Монастирського, к.т.н. В.І. Кузьменко, к.т.н. Ю.І. Григор'єва, к.т.н. Е.Х. Завгороднього, к.т.н. В.Т. Полуніна, к.т.н. В.Н. Григор'єва та багатьох інших учених, як у нашій країні, так і за кордоном. Цим питанням займаються такі організації як: Санкт-Петербурзький Державний Університет, Запорізький національний технічний університет, Донецький національний технічний університет, ТОВ «Гірський інститут» міста Дніпропетровськ, ВНІІПТМАШ і т.д.
Мета і завдання роботи
Мета роботи: провести аналіз впливу параметрів стикового клейового з'єднання на його напружено деформований стан, використовуючи моделювання в програмному середовищі SolidWorks 2004 з інтегрованим розрахунковим модулем CosmosWorks 2004 з застосуванням методу планування експерименту, що дозволить обґрунтувати довжину нахлесту, знизивши при цьому витрати на виготовлення стику.
Завдання:
- Проаналізувати методи, що використовуються в холодній вулканізації стиків конвеєрної стрічки;
- Застосувати сучасне програмне забезпечення для розрахунків моделі клейового стику конвеєрної стрічки;
- Побудувати графіки залежностей внутрішніх напружень від властивостей клейового шару;
- Скласти розширені матриці планів експериментів;
- Застосувати метод розрахунку елементарних конструкцій композиційних матеріалів до досліджуваної моделі;
Прогнозовані результати роботи
Дана робота спрямована на вивчення факторів, що впливають на міцність стикового з'єднання. Планується отримати залежності і математичну модель напружено-деформованого стану стикового з'єднання конвеєрної стрічки. Отримати детальний аналіз факторів взаємодії клейового шару з тканинної прокладкою стику.
Побудова фізичної моделі досліджуваного зразка
Сучасні комп'ютерні технології дозволяють нам все простіше моделювати і розраховувати різні механічні системи. Для реалізації цього існує досить таки велика кількість програмних середовищ працюють у тому чи іншому напрямі. У даній роботі була обрана програма для побудови 3D моделі і проведення розрахунку на міцність - SolidWorks 2004 з вбудованим модулем розрахунковим CosmosWorks 2004.
Побудова фізичної моделі включає в себе ідеалізацію властивостей конструкції і зовнішніх впливів. У загальному випадку конструкція, виготовлена з реального матеріалу, що знаходиться під дією зовнішніх навантажень, може мати багато особливостей, що включають у себе недосконалість форми, несплошність і неоднорідність властивостей матеріалу, особливо в характері зовнішнього навантаження і т.п. У практичних розрахунках врахувати всі наявні особливості конструкції, матеріалу і навантаження неможливо. Звичайно, залучення ЕОМ розширило можливості обліку в міцнісних розрахунках деяких з перерахованих вище особливостей, але необхідно розуміти, що як би не були великі потужності сучасних ЕОМ, їх швидкодію й обсяг пам'яті, але й вони не безмежні. Тому, приступаючи до практичних розрахунками, ми змушені підміняти реальні тіла деякими ідеалізованими об'єктами - «механічними моделями».
Реальне тіло, яке представляє гумовотканинну стрічку, можна розглянути як нескінченну систему матеріальних точок, певним чином взаємодіють між собою. З точки зору атомної будови речовини і існування сил міжатомної взаємодії кожної з матеріальних точок властива певна індивідуальність. Однак простежити за станом кожної з матеріальних точок зовсім неможливо, тому доводиться вводити деякі осереднені характеристики, які описують взаємодію між атомами, відмовившись від розгляду кожного атома в окремо (статистична фізика). Для опису поведінки тіла відомості про їх атомної структурі не потрібні. Реальне тіло замінюється уявної (модельної) суцільний середовищем. Середа називається суцільний, якщо будь-який обсяг, виділений з неї, містить речовину. Таке уявлення про суцільну середовищі суперечить уявленню про атомному будову речовини, проте воно надзвичайно спрощує математичний опис поведінки твердих тіл під дією прикладеного навантаження.
Ще однією ідеалізацією реального тіла є присвоєння йому властивостей однорідності. Середа називається однорідною, якщо властивості виділених з неї малих обсягів однакові. Природно, тут мова йде про тих властивостях, які визначаються шляхом механічного експерименту. Певною ідеалізації піддається також і поняття «зовнішні сили». У механіці передбачається, що сила повністю визначена, якщо задано відповідний вектор, при цьому сила розглядається як результат взаємодії двох твердих тіл. З цієї точки зору вектор сили, що діє на поверхню тіла, означає зосереджену силу, тобто силу, прикладену в точці. Проте, насправді, «зосереджених» сил не існує.
Рисунок 1 - Габаритні розміри моделі досліджуваного зразка
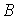- ширина стикуємих елементів,
- довжина тканинної прокладки,
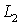- довжина клейового шару,
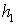- товщина клейового шару,
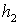- товщина тканинної прокладки.
Значення параметрів досліджуваної моделі: 
, 
, 
, 
, 
.
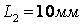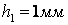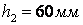Розбиття 3D моделі досліджуваного зразка на кінцеві елементи
Основна ідея методу кінцевих елементів полягає в тому, що будь-яку безперервну величину (переміщення, температура, тиск і т.п.) можна апроксимувати моделлю, що складається з окремих елементів (ділянок). На кожному з цих елементів досліджувана безперервна величина апроксимується кусково-неперервної функції, яка будується на значеннях досліджуваної безперервної величини в кінцевому числі точок розглянутого елемента (рис. 2).
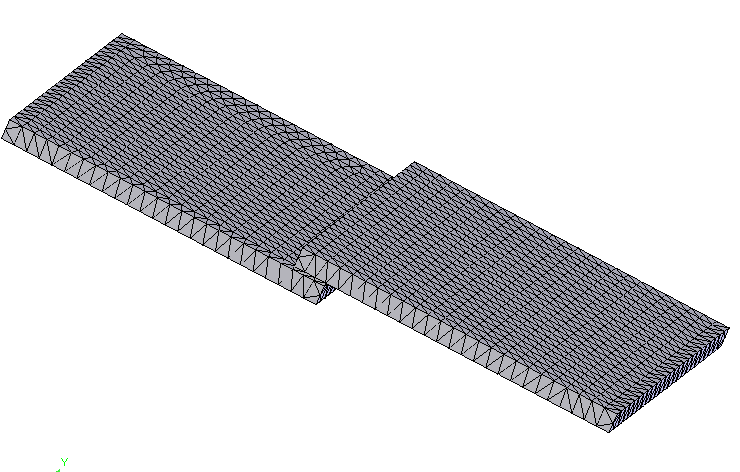
Рисунок 2 - Застосування МКЕ до розглянутої моделі
Додаток сили обмежень до досліджуваної моделі
Досліджувана модель має наступні граничні умови і додані сили: зафіксована одним торцем тканинної прокладки (імітує жорстке закріплення у розривній машині), а з іншого боку, додана розподілене навантаження по всій поверхні торця (рис. 3).
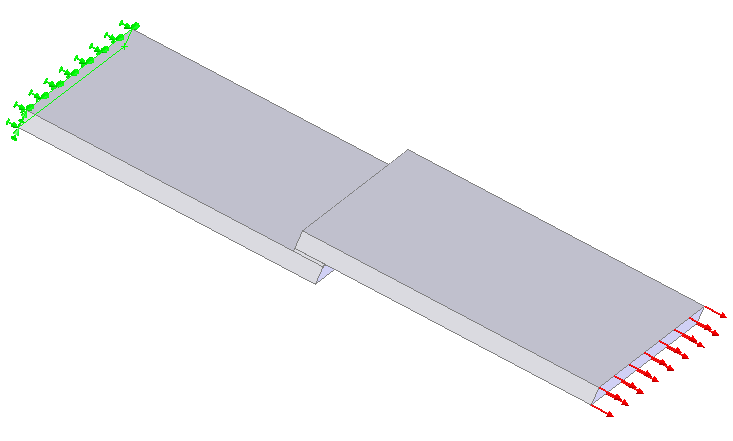
Рисунок 3 - Схема прикладання сил і граничних умов до досліджуваного зразку
Представлення результатів розрахунку
Результати розрахунку з чисельних моделями радикально відрізняються від результатів аналітичних обчислень. Величина і спосіб інтерпретації останніх, як правило, однозначні. Чисельні ж методи для приблизно поставленої задачі, розв'язаної непрямими алгоритмами, дають оцінку, яка може бути вельми неоднозначно витлумачена. А отже, інтерпретація результатів застосування алгоритмів типу МСЕ - заняття неформальне, що вимагає певного розуміння істоти явища.
На основі розрахунків нами були отримана епюри напружено деформованого стану клейового стику гумовотканинні конвеєрної стрічки, представлена на рисунку 4. У ній представлені внутрішні напруження в кожному з вузлів елементів. Результати відображаються за допомогою кольорової палітри: синій колір вказує на мінімальне значення напружень, а червоний - на максимальні.
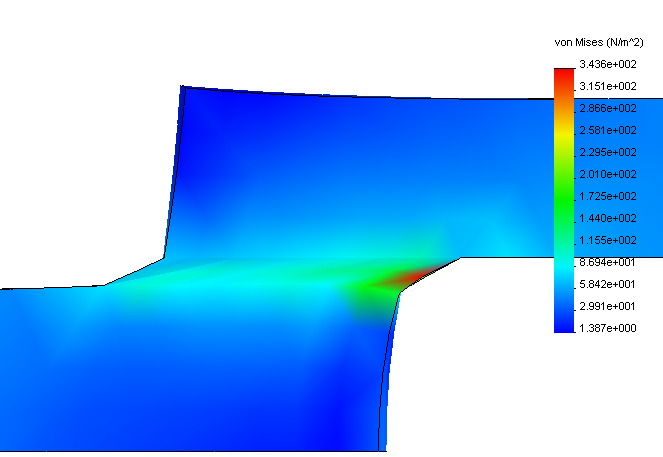
Рисунок 4 - Eпюри внутрішніх напружень в досліджуваному зразку
Аналізуючи епюри наведену на малюнку 4 слід, що критичні напруги, які можуть призвести до руйнування, знаходяться в середині клейового шару.
ДОСЛІДЖЕННЯ НАПРУЖЕНО-ДЕФОРМОВАНИЙ СТАН ЕЛЕМЕНТАРНІ ВЗАЄМОДІЇ У СИСТЕМІ «ПРОКЛАДКОЮ - КЛЕЙОВИЙ ШАР - ПРОКЛАДКИ»
Для дослідження елементарної системи «тканинна прокладка - клейовий шар - тканинна прокладка» було застосовано метод планування експерименту. Даний спосіб обробки даних дозволяє підвищити продуктивність праці та надійність отриманих результатів. Оскільки цей експеримент багатофакторний і пов'язаний з відшукання оптимальних умов нами був застосований метод повного факторного експерименту типу 2^k, що дозволить досить повно вивчити поведінку системи в значному числі експериментів.
Локальну область визначення факторів встановимо з апріорних міркувань. У ході експерименту фактори варіювалися на двох рівнях. Інтервали варіювання, а так само їх значення на основному, верхньому і нижньому рівнях наведені в таблиці 4.1. Основний рівень є вихідною точкою для побудови плану експерименту, а інтервали варіювання визначають відстані до нього по осях координат від верхнього і нижнього рівнів.
Таблиця 4.1 - Рівні факторів
| Фактори | P, Н/м^2 | V | E, МПа | L2, мм | h1, мм |
| Основний рівень (Xio) | 125 | 0,4925 | 6,55 | 15 | 1,5 |
| Інтервал варіювання (deltaXi) | 25 | 0,0025 | 0,45 | 5 | 0,5 |
| Верхній рівень (Хi = +1) | 150 | 0,495 | 7 | 20 | 2 |
| Нижній рівень (Хi = -1) | 100 | 0,49 | 6,1 | 10 | 1 |
Число дослідів в нашому випадку становитиме:
Кодований і натуральні значення факторів знайдемо використовуючи формулу і занесемо в таблицю 2.
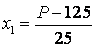
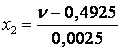
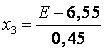
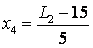
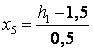
Результатом є значення факторів, рівні +1 (верхній рівень) і -1 (нижній рівень).
Таблиця 2 - Матриця плану експерименту
Рівняння регресії для k = 5 має вигляд:
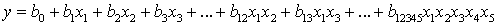
Лінійні коефіцієнти регресії розраховуються за формулою:
Коефіцієнт регресії, що характеризує парне взаємодія факторів, знаходять за формулою:
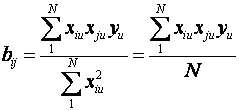
Складання математичної моделі у відносних одиницях
Використовуючи отримані значення, на підставі рівняння регресії (4.7) складемо математичну модель:
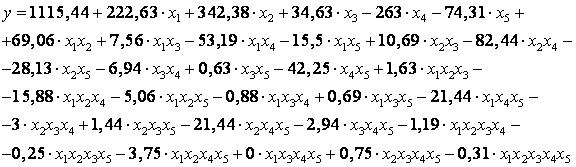
Найменші значення функції вдалося досягти при нижньому рівні P, V і Е і верхньому рівні L2 і h1. Тобто саме міцне з'єднання при функції
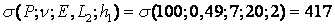
Вплив досліджуваних факторів на критичні напруги в клейовому з'єднанні
Для побудови графіків, що описують вплив досліджуваних факторів на внутрішні напруження в клейовому стику гумовотканинні стрічки, виходячи з крайніх значень кордонів чинників були отримані процентні показники максимального і мінімального зміни факторів по відношенню до нульового рівня. Значення внутрішніх напружень на цих кордонах по відношенню до значення в нульовій точці показує на скільки даний фактор впливає на параметр оптимізації в з'єднанні.
Рисунок 5 – Вплив досліджуваних факторів на критичні напруги
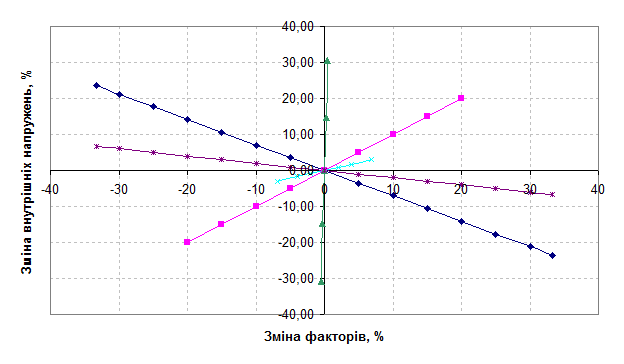
Рисунок 6 – Вплив досліджуваних факторів на ступінь зміни параметра оптимізації
Виходячи з отриманих даних на малюнках 5 та 6 зробимо наступні висновки:
- Найбільший вплив на максимальне значення внутрішніх напружень надає коефіцієнт Пуассона. При зміні цього параметра на 0,5% значення параметра оптимізації змінюються на 30%.
- Найменший вплив в досліджуваних межах зробило висота клейовий плівки.
- Фактор розподіленого навантаження справив на модель лінійне вплив - при збільшенні його на 20%, внутрішні напруги також збільшуються на 20%.
- Модуль Юнга значно не вплинув на досліджувану модель.
- Довжина клейовий плівки L2 істотно впливає на параметр оптимізації. При збільшенні довжини на 1 / 3 міцність стику збільшується на 23,6%.
ДОСЛІДЖЕННЯ ВПЛИВУ КУТА СКОСУ СТИКІВ ГУМОВОТКАНИННІ КОНВЕЄРНОЇ СТРІЧКИ НА ЙОГО НАПРУЖЕНО-ДЕФОРМОВАНИЙ СТАН
Резервом підвищення міцності стику є косою зріз його ступенів по відношенню до поздовжньої осі стрічки під кутом alfa. При цьому напруги в каркасі стрічки і в гумових прошарках розподіляється на велику довжину і їх абсолютна величина знижується. Досвід експлуатації показує, що у разі косого ступенів поліпшуються умови входу стику на барабани і ролики конвеєра, значно підвищується надійність з'єднань, що особливо помітно при експлуатації дорогих, високоміцних стрічок на конвеєрних лініях великої протяжності і продуктивності.
Дослідження впливу кута скосу на НДС стику стрічки
За допомогою методів, викладених у 2 чолі, проведемо моделювання деталей стиків стрічок, з різним кутом скосу. Потім проаналізуємо їх напружено деформований стан в клейовому шарі.
Досліджуваний діапазон кутів скосу - від 0° до 45°. Досліджуємо напружено-деформований стан клейового шару при різних розтягуючих силах.
Це буде виглядати наступним чином:
Рисунок 7 – Модель стику стрічки при куті скосу 0° (45°)
Таблиця 4 – Внутрішня напруга в клейовому шарі.
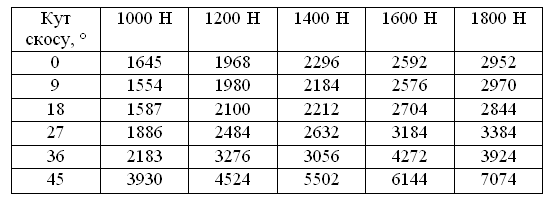
Динаміку зміни внутрішньої напруги в стику конвеєрної стрічки, в залежності від кута скосу можна побачити на рисунку 8.
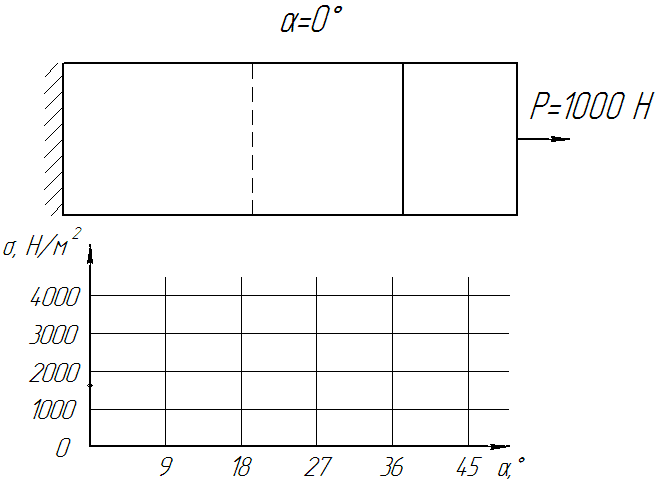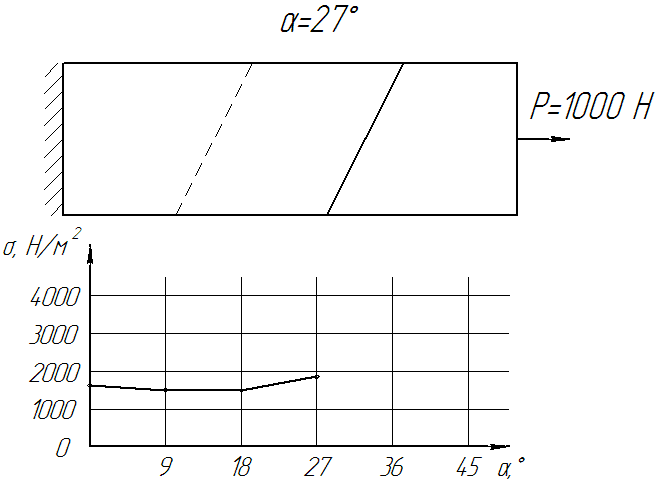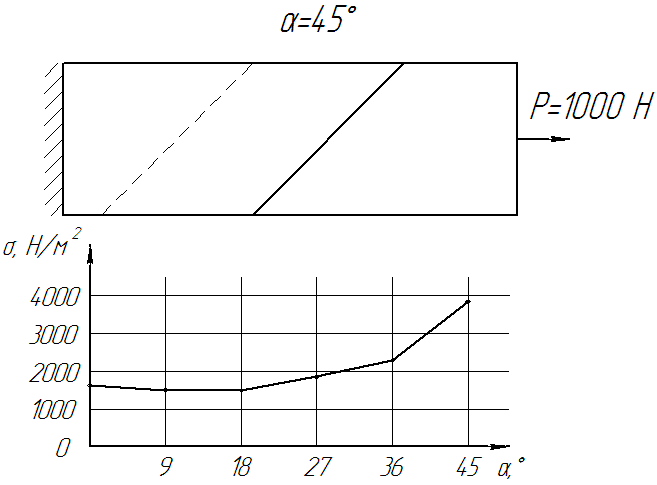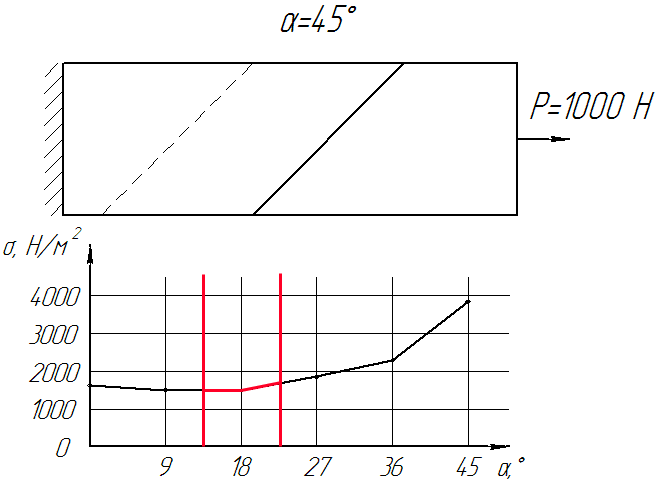
Рисунок 8. - Динаміка зміни напруги від кута скосу стику (Кількість кадрів: 12, кількість циклів: нескінченне, затримка: 75 мс, розмір файлу: 92,2 КБ)
За отриманими даними побудуємо графіки напружено деформованого стану клейового стику стрічки.
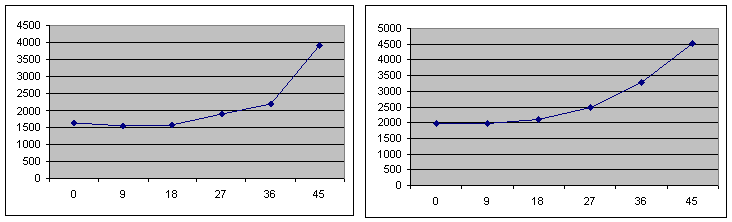
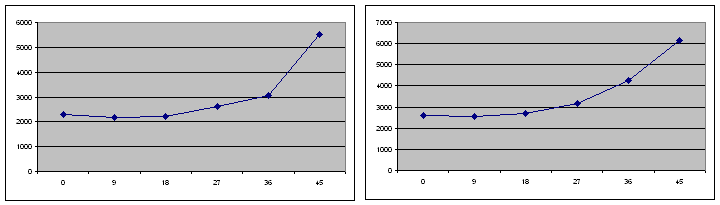
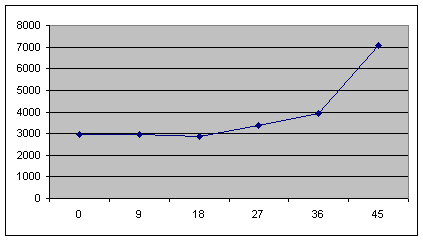
Рисунок 9. – Графіки розподілу напруги при 1000, 1200, 1400, 1600, 1800 Н
З отриманих графіків слід чітка залежність розподілу напружено-деформованого стану клейового шару стику залежно від кута скосу стику. Приблизно до кута 20° спостерігається практично прямолінійний зростання напружено деформованого стану всередині клейового стику стрічки, а потім значний його зростання. Самий оптимальний кут скосу (з ПДВ) знаходиться в межах від 12° до 20°.
При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2010. Повний текст роботи по темі можуть бути отримані у автора або його наукового керівника після вказаної дати.
Література
- Высочин Е.М. Стыковка и ремонт конвейерных лент на предприятиях черной металлургии/ Е.М. Высочин, Е.Х. Завгородний, В.И. Заренков. - М.: Металлургия, 1989, с. 192.
- Билан И.Е. О прочности связи между слоями резинотканевых конвейерных лент – В кн. Вопросы рудничного транспорта, в.9./ И.Е. Билан. - М.: «Недра». 1965 – с. 54-62.
- Билан И.Е. Макро- и микроисследования конвейерных лент. – В кн.: Вопросы рудничного транспорта, в.8/ И.Е. Билан. - М.: «Недра», 1965 – с. 23-37.
- Монастырский Д.Ш. Об изменении прочности связи между прокладками резинотканевых конвейерных лент по толщине. – В кн.: Вопросы рудничного транспорта, в.12/ Д.Ш. Монастырский. - М.: «Недра», 1972 – с. 60-69.
- Алямовский А.А. SolidWorks/CosmosWorks. Инженерный анализ методом конечных элементов/ А.А. Алямовский. – М.: ДМК Пресс, 2004. – 432 с.: ил.
- Агапов В.П. «Метод конечных элементов в статике, динамике и устойчивости пространственных тонкостенных подкрепленных конструкций». учебное пособие/ В.П. Агапов. - М.: изд. АСВ, 2000, 152 стр., с илл.
- Хамханов К.М. Методическое пособие: Основы планирования эксперимента/ К.М. Хамханов. - Улан-Уде, 2001.
- Якушев В. Л. Применение 3D-конечных элементов для расчета тонкостенных конструкций: [Електронний ресурс]. - Режим доступу: http://www.ipdn.ru/rics/vk/1VK-yak.pdf
- Шимановский А. О. «Применение метода конечных элементов в решении задач прикладной механики: [Електронний ресурс]. - Режим доступу: http://www.belsut.gomel.by/Ellibrary/1/70.pdf