Левчик ЮВ Моделирование напряженно-деформированного состояния клеевого стыка конвейерной ленты с использованием метода конечных элементов

УДК 621.86

Ю. В. Левчик, специалист,

А. Я. Грудачев, канд. техн. наук, проф.,

Донецкий национальный технический университет

МОДЕЛИРОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ КЛЕЕВОГО СТЫКА КОНВЕЙЕРНОЙ ЛЕНТЫ С ИСПОЛЬЗОВАНИЕМ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ

Проблема и ее связь с научными и практическими задачами.

Лента и особенно ее стыковое соединение являются наиболее уязвимыми элементами конвейера. От их прочности зависят технические и экономические показатели установки. Ежегодно на предприятиях отрасли изготавливается более 75 тыс. стыковых соединений, что приводит к значительному расходу конвейерных лент и потерям рабочего времени. Преждевременное разрушение стыков приводит к аварийным остановкам транспортных линий, устранение которых трудоемко и связано со значительными затратами [1].

Анализ исследований и публикаций.

Научные основы теории совершенствования конструкций и методов расчета стыковки резинотканевых лент конвейеров посвящены исследования проф., д.т.н. В.Г. Дмитриева, проф., д.т.н. И.Г. Штокмана, к.т.н. Е.М. Высочина, проф., к.т.н. Д.Ш. Монастырского, к.т.н. В.И. Кузьменко, к.т.н. Ю.И. Григорьева, к.т.н. Е.Х. Завгороднего, к.т.н. В.Т. Полунина, к.т.н. В.Н. Григорьева и многих других ученых, как в нашей стране, так и за рубежом. Данным вопросом занимаются такие организации как: Санкт-Петербургский Государственный Университет, Московский горный университет, Запорожский национальный технический университет, Донецкий национальный технический университет, Днепропетровская национальная горная академия, ВНИИПТМАШ и т.д.

Постановка задачи.

Для разработки и исследования математической модели напряжено-деформированного состояния клеевого стыка конвейерной ленты были поставлены следующие задачи:

проанализировать методы используемые в холодной вулканизации стыков конвейерной ленты;
применить современное программное обеспечение для расчетов модели клеевого стыка конвейерной ленты;
составить уравнения регрессии с 5-ю переменными;
составить математические модели напряженно-деформированного состояния исследуемых моделей клеевых стыков конвейерной ленты;

Изложение материала и результаты.

Эксперименты связанные с разрывом стыков лент требуют соответствующее оборудование, а так же материальных затрат. Создание конструкций такого типа невозможно без совершенствования и автоматизации процесса проектирования, применения новых материалов и технологий. Естественно, что при создании модели сложной конструкции, например которой можно считать клеевой стык резинотканевой ленты, прибегают к некоторой идеализации ее формы.

Для таких расчетов нами были выбраны современные программные среды для расчета напряженно-деформированного состояния тел. К ним относятся ANSYS, COSMOS SolidWorks, AutoCAD Mechanical Desktop и др. Математической основой, на которой построены вычислительные аппараты этих программных продуктов, является метод конечных элементов (МКЭ) [2].

Физическая модель может быть наделена лишь частью свойств реальной конструкции, а поэтому – проще ее математическое описание. От того, насколько удачно выбрана физическая модель конструкции, зависит, в конечном итоге, трудоемкость расчета и точность его результатов. Нами был исследован образец резинотканевой ленты (рис. 1) со следующими габаритными параметрами: B - ширина стыкуемых элементов, L1 - длина тканевой прокладки, L2 - длина клеевого слоя, h1 - толщина клеевого слоя, h2 - толщина тканевой прокладки.

Рисунок 1 – Габаритные размеры модели исследуемого образца

Начальной стадией расчета является разбиение 3D модели клеевого стыка конвейерной ленты методом конечных элементов. В МКЭ все виды нагрузок включающие распределенные поверхностные нагрузки, объемные силы, сосредоточенные силы и моменты приводятся к сосредоточенным силам, действующим в узлах. Основная идея метода конечных элементов состоит в том, что любую непрерывную величину, например перемещение, температура, давление можно аппроксимировать моделью, состоящей из отдельных элементов. На которых исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, которая строится на значениях исследуемой непрерывной величины в конечном числе точек рассматриваемого соединения [3].

Вторым этапов было наложение сил и ограничений на расчетную модель, после чего выполнялся непосредственно сам расчет. Она имеет следующие граничные условия и приложенные силы: зафиксирована одним торцом тканевой прокладки (имитирующая жесткое закрепление в разрывной машине), а с другой стороны приложена распределенная нагрузка по всей поверхности торца элемента. В результате расчета в программной среде CosmosWorks 2004 нами были получены эпюры деформированной расчетной модели в которой цветовой диапазон зависит от уровня напряжений в рассматриваемом клеевом стыке приведенном на рисунке 2.

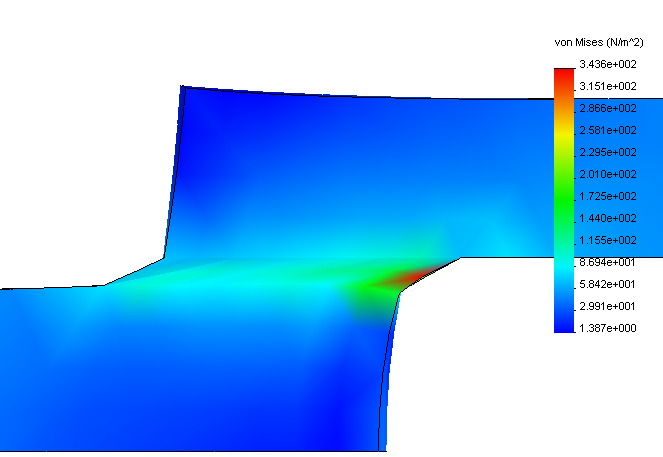
Рисунок 2 – Эпюра напряженно-деформированного состояния клеевого стыка

На основании проделанных опытов были построены диаграммы зависимостей внутренних напряжений в клеевом стыке исследуемой модели от ряда факторов: распределенной нагрузки, коэффициента Пуассона, модуля Юнга и др.

Полученные экспериментальные данные напряженно-деформированного состояния модели стыка конвейерной ленты были обработаны методом полного факторного эксперимента типа 2^k [4].

В качестве отклика Y было выбрано значение внутренних напряжений в клеевой пленки. Априорно в число факторов, влияющих на параметр оптимизации были включены: Р – распределенная нагрузка, приложенная к тканевой прослойке, Н/м^2; V – коэффициент Пуасонна клеевой пленки; Е – модуль Юнга, МПа; L2 – длина клеевой пленки, мм; h1 – высота клеевой пленки, мм. Локальную область определения факторов установим из априорных соображений. В ходе эксперимента факторы варьировались на трех уровнях: основной, верхний и нижний. Основной уровень является исходной точкой для построения плана эксперимента, а интервалы варьирования определяют расстояния по осям координат до верхнего и нижнего уровней. Была проведено 32 опыта, которые не дублировались.

В соответствии с методом полного факторного эксперимента исследуемые факторы были закодированы путем линейного преобразования координат факторного пространства с переносом начала координат в нулевую точку и выбором масштабов по осям в единицах интервалов варьирования факторов. Далее рассчитаны коэффициенты регрессии: свободный член; линейные; двойного, тройного и т.п. взаимодействий.

Используя полученные значения коэффициентов регрессии было составлено уравнение регрессии, физический смысл которого заключается в соотношении показывающем взаимосвязь внутренних напряжений от ряда факторов:

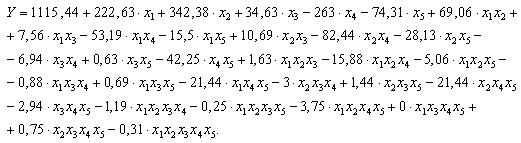
Для проверки адекватности полученной модели подставим кодированные значения исследуемых факторов для каждого из опытов. Полученные значения величин ошибок незначительны и не превышают 3%. На основании вышеизложенного сделан вывод об адекватности данной математической модели.

Для удобства применения данной математической модели был выполнен переход от кодированных значений к натуральным. Преобразованная математическая модель имеет следующий вид:

Полученная математическая модель позволит упростить решение задач автоматизации проектирования и расчета композитных материалов.

Выводы и направления дальнейших исследований.

Обзор литературы показал, что в настоящее время недостаточно раскрыт вопрос расчета и проектирования клеевого стыка резинотканевой конвейерной ленты на ЭВМ при помощи современных программных продуктов, таких как ANSYS, SolidWorks и др.
Применение современного программного продукта SolidWorks 2004 позволило рассчитать клеевой стык резинотканевой конвейерной ленты. Результаты опытов, проведенные на ПК, показали, что критические внутренние напряжения находятся на краю клеевой пленки в средней плоскости.
Для анализа массива опытных данных проведена статистическая обработка при помощи метода полного факторного эксперимента типа 2^k. Построены математические модели ступенчатого клеевого стыка резинотканевой конвейерной ленты в кодированных и в именованных единицах. Отклонения параметра оптимизации от экспериментальных значений в полученных уравнениях не превышают 2%.

Список источников:

Высочин Е.М. Стыковка и ремонт конвейерных лент на предприятиях черной металлургии/ Е.М. Высочин, Е.Х. Завгородний, В.И. Заренков. - М.: Металлургия, 1989, с. 192.
Алямовский А.А. SolidWorks/CosmosWorks. Инженерный анализ методом конечных элементов/ А.А. Алямовский. – М.: ДМК Пресс, 2004. – 432 с.: ил.
Агапов В.П. «Метод конечных элементов в статике, динамике и устойчивости пространственных тонкостенных подкрепленных конструкций». учебное пособие/ В.П. Агапов. -М.: изд. АСВ, 2000, 152 стр., с илл.
Хамханов К.М. Методическое пособие: Основы планирования эксперимента/ Сост. К.М. Хамханов. -Улан-Уде: 2001.