В. Л. Якушев, И. А. Сумароков
ПРИМЕНЕНИЕ 3D-КОНЕЧНЫХ ЭЛЕМЕНТОВ ДЛЯ РАСЧЕТА ТОНКОСТЕННЫХ КОНСТРУКЦИЙ
Введение
Тонкостенные элементы конструкций широко распространены в современной технике, обеспечивают высокую надежность и прочность конструкций при их легкости. У них один или два размера значительно меньше других. Благодаря этой особенности удается на основе гипотез, например, Кирхгофа — Лява или Тимошенко уменьшить размерность задачи и тем самым упростить уравнения, описывающие деформации. Вместо трехмерных уравнений механики деформируемого твердого тела (МДТТ) получаем двух- или одномерные задачи. Теория стержней пластин и оболочек достаточно хорошо обоснована, определена область их применения, разработаны универсальные методы решения задач при различных условиях закрепления и нагружения [2, 3, 6], накоплен большой практический опыт в проектировании таких конструкций.
Вместе с тем при уменьшении размерности задачи расчет для некоторых областей реальной тонкостенной конструкции нельзя признать достоверным. К ним относятся места закреплений, приложения сосредоточенных сил, пересечения тонкостенных элементов, места, где толщина сравнима с радиусами кривизны. Плохо обоснованным представляется применение указанных выше гипотез в областях с пластическими зонами. Все это приводит к уменьшению достоверности расчетов и необходимости увеличивать запас прочности.
Выход из этой ситуации можно найти только при использовании трехмерных уравнений МДТТ либо для всей расчетной области, либо для тех ее частей, в которых теория тонкостенных конструкций может давать заведомо неправильные результаты [3]. Но это ведет к резкому росту объема вычислений. Так, в работе [4] дается оценка трудоемкости решения задач МДТТ, согласно которой повышение размерности задачи на единицу увеличивает объем вычислений в 1000 раз. В статье [5] указывается, что «реализовать на практике эту принципиальную возможность (имеется в виду решение задач механики оболочек в трехмерной постановке) в требуемом объеме не удается вследствие чрезмерной сложности решения трехмерных задач и большого разнообразия практически необходимых постановок задач». Уменьшение отношения толщины к характерному размеру приводит к ухудшению сходимости решения, и приходится использовать очень мелкие сетки.
Однако если теория оболочек ввиду ее принципиальной ограниченности из-за применения различных гипотез не может обеспечить необходимую достоверность расчетов, то развитие вычислительной техники приводит к облегчению больших объемов вычислений. Многие задачи уже сейчас могут быть решены в трехмерной постановке.
В настоящее время разработано большое количество универсальных пакетов на основе метода конечных элементов (МКЭ), позволяющих решать широкий класс задач механики сплошных сред: гидро- и газодинамики, деформируемого твердого тела, совместных задач и т. п. При этом от пользователя требуются высокая квалификация и выполнение большого объема работы по подготовке исходных данных для решения задачи, ему необходимо изучить значительное количество технической документации для ознакомления с основными принципами работы пакета программ. В качестве примеров таких пакетов можно назвать «NASTRAN», «ANSYS», «Cosmos», «ASKA», «ADINA» и др.
Относительно новое направление в разработке программного обеспечения на основе МКЭ — создание специализированных пакетов, ориентированных на решение узкого класса задач. Достоинствами этих пакетов являются низкая стоимость и простота правил использования.
Далее дается описание алгоритма расчета напряженно-деформированного состояния в месте соединения двух цилиндрических труб МКЭ с различными диаметрами, углами пересечения и граничными условиями.
1. Вариационная формулировка задачи
Рассмотрим вариационную формулировку трехмерной задачи теории упругости. Если задача решается в перемещениях и на контуре заданы их значения, то необходимо минимизировать потенциальную энергию системы. Если задача решается в напряжениях с заданными на границе усилиями, то следует минимизировать дополнительную работу системы. Общепринятая формулировка МКЭ предполагает отыскание полей перемещений и, как результат, минимизацию потенциальной энергии системы при отыскании узловых значений вектора перемещений. После того как перемещения будут определены, можно вычислить компоненты тензоров деформаций и напряжений [3].
Рассмотрим деформируемое тело, занимающее в пространстве x1, x2, x3 область V , ограниченную поверхностью S . Материал будет считаться упругим, изотропным и однородным. Перемещения в теле обозначим как u1(x1, x2, x3), u2 (x1, x2, x3), u3 (x1, x2, x3) компоненты тензора деформаций — как ![]()
Согласно принципу возможных перемещений для сплошных сред, работа всех внутренних и внешних сил на малых возможных перемещениях точек тела из состояния его равновесия равна нулю. Возможными перемещениями u являются любые малые отклонения, которые удовлетворяют условиям непрерывности тела и условиям перемещений на поверхности тела.
В общем случае трехмерной деформации работа всех внешних сил на малых возможных перемещениях равна изменению потенциальной энергии деформации тела:

де W — удельная потенциальная энергия деформации, которая равна свободной энергии при изотермическом процессе деформирования и внутренней энергии при адиабатическом деформировании; p — плотность; ![]() - массовые силы; t — вектор внешних поверхностных сил с компонентами ti (1,2,3) i = . Для вариации W cправедливо
- массовые силы; t — вектор внешних поверхностных сил с компонентами ti (1,2,3) i = . Для вариации W cправедливо
Областью интегрирования в последнем интеграле является та часть поверхности, где не заданы условия перемещения. Знак вариации в (1.1) можно вынести за знаки интегралов, тогда

Уравнение (1.3) называется вариационным уравнением Лагранжа.
В случае линейно-упругого тела W (Eij) представляет собой положительно-определенную квадратичную форму
2. Криволинейный 20-узловой КЭ
Далее будем рассматривать КЭ в виде фигур с шестью криволинейными боковыми гранями. Пусть в каждом КЭ введена естественная (локальная) система координат r, s , t, которая является ортогональной, и -1< r <+1, -1< s <+1, -1< t <+1, тогда в них КЭ представляет собой куб.
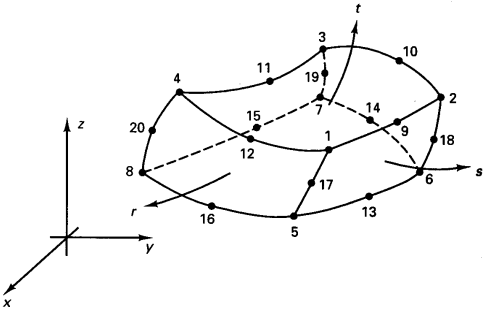
Рис. 1. Криволинейный трехмерный конечный элемент с переменным количеством узлов от 8 до 20
Рассмотрим квадратичный 3D КЭ с 20 узлами [3, 6] (рис. 1), для которого определены функции формы hi=ho(r, s, t), i — локальные номера узлов:

Координаты узлов КЭ обозначим как X1i, X2i, X3i (i=1...20). Тогда преобразование от глобальной системы координат к естественной для рассматриваемого КЭ записывается следующим образом:

На основании этих формул можно вычислить производные из (2.3) по естественным координатам каждого КЭ:
В изопараметрическом КЭ перемещения аппроксимируются аналогично преобразованию координат через их значения в узлах U1i, U2i, U3i (i=1...20):
В этом КЭ число узлов может меняться от 8 до 20. Если какой-либо узел с номером от 9 до 20 исключается, то в (2.2) соответствующие величины gi обнуляются. Благодаря этому можно получить ряд переходных элементов от трехмерного тела к оболочечному КЭ, как описано в [3]. На основании полученных формул можно найти распределение деформаций и напряжений внутри КЭ как функции узловых перемещений. После их подстановки в (1.3) задача сводится к системе линейных алгебраических уравнений относительно узловых перемещений, а правая часть зависит от приложенных нагрузок.
3. Расчет напряженно-деформированного состояния двух пересекающихся труб
Описанный выше КЭ позволяет, как из кирпичей, строить разнообразные расчетные области. В частности, он был использован при разработке пакета прикладных программ для расчета напряженно-деформированного состояния двух пересекающихся труб (рис. 3) с различными диаметрами и углами пересечения. Допускается наличие усиления вокруг патрубка, на самом патрубке и сварных швов. Конструкция нагружена внутренним давлением, к концу патрубка приложены силы и моменты.
С помощью данного пакета можно рассматривать только указанную задачу, но при этом практически сразу приступить к ее решению, так как в интерфейсе содержится вся необходимая для формулировки задачи информация, проводится проверка правильности ввода исходных данных и от пользователя не требуется знание основных принципов МКЭ. После решения задачи можно сразу проанализировать результаты и, если необходимо, повторить ее решение с новыми исходными данными.
Интерфейс программы (рис. 2) дает возможность как создавать новые, так и загружать ранее созданные проекты. Все необходимые для расчетов данные разбиты на две группы: геометрические и физические; пользователь видит чертеж, на котором отмечены все требуемые размеры и их обозначения.

Рис. 2. Окно интерфейса для ввода исходных данных
Программа позволяет проанализировать геометрическую модель, разбиение на конечные элементы (рис. 4). При необходимости можно скорректировать некоторые размеры и параметры сетки КЭ. После этого наступает этап расчета, по завершении которого можно получить полную информацию о напряженно-деформированном состоянии рассматриваемой конструкции, изменить число линий уровня, а также выбрать параметры вывода (отображение сетки, наличие линий уровня). Доступны опции увеличения, вращения трехмерного объекта, позволяющие изучить его с любой стороны, и получения сечений.
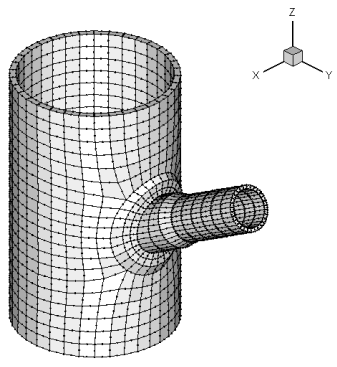
Рис. 3. Конечно-элементная модель для расчета НДС двух пересекающихся труб
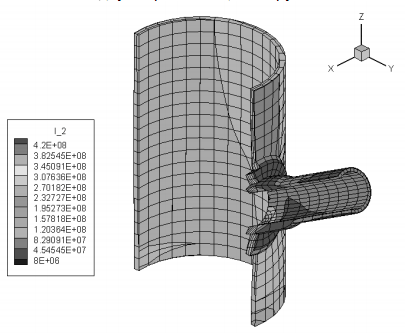
Рис. 4. Распределение интенсивности тензора напряжений при нагружении внутренним давлением (Пa)
Интерфейс пакета программ написан на языке C++, для работы с графикой использован OpenGL.
Созданный пакет может быть относительно просто перестроен на расчет других конструкций.
ЛИТЕРАТУРА
- Бекетова Е.А. Разработка интерфейса для специализированного пакета программ на основе метода конечных элементов/ Е.А. Бекетова // Тр. XLVIII науч. конференции Московского физико-технического института (государственного университета). Современные проблемы фундаментальных и прикладных наук. — М.: Долгопрудный, 2005. — № 7. — С. 153–154.
- Голованов А.И. Введение в метод конечных элементов статики тонких оболочек/ А.И. Голованов, М.С. Корнишин. —Казань: 1990. — 269 с.
- Голованов А.И. Метод конечных элементов в механике деформируемых тел/ Д.В. Бережной —Казань: Изд-во «ДАС», 2001. — 301 с.
- Михлин С.Г. Вариационные методы в математической физике/ С.Г. Михлин —М.: Наука, 1970.
- Пикуль В.В. Современное состояние и перспективы развития теории оболочек/В.В. Пикуль// Проблемы механики сплошных сред и элементов конструкций: Сб. науч. тр. — Владивосток: Дальнаука, 1998. — С. 27–44.
- Bathe K.-J. The finite element procedures. — Prentice-Hall, Upper Saddle River, N. J., 1996. — 1037 p.