
Метод ФАПЧ и принципы синтезирования высокочастотных сигналов
Источник: http://www.chipinfo.ru/literature/chipnews/200106/7.htmlacademic.ru/dic.nsf/ruwiki/1159408
Система фазовой автоматической подстройки частоты, далее ФАПЧ (зарубежная аббревиатура Phase - Locked Loop, PLL), представляет собой самостоятельный узел, входящий в состав различной аппаратуры связи, систем спутникового вещания и передачи данных, а также в состав устройств, являющихся стабильными источниками сигналов.
Первая система ФАПЧ была разработана в 1930 году французским инженером Беллизом. Однако широкое применение она получила в 1960 году с появлением первых интегрированных ФАПЧ компонентов. Существовало традиционное предубеждение против ФАПЧ, связанное отчасти со сложностью реализации её на дискретных компонентах, а отчасти - с сомнениями относительно надёжности её работы. Со временем, когда стали появляться высокоинтегрированные компоненты, реализующие на одном кристалле практически все необходимые (за исключением некоторых внешних элементов) узлы ФАПЧ, эта система, при правильном и корректном проектировании, стала достаточно надёжным и заслуживающим внимания узлом.
Систему ФАПЧ можно представить как систему с отрицательной обратной связью, содержащую коэффициент усиления в прямом направлении G(s) и коэффициент обратной cвязи H(s), а также значение e(s), характеризующее разностный сигнал между входным сигналом Vi и сигналом цепи обратной связи V0.
GCL - коэффициент передачи замкнутого контура (от Gain Closed Loop), где - комплексное число, характеризующее круговой вектор, а - круговая частота.
Фазовый детектор PD (Phase Detector) производит сравнение двух частотных сигналов и формирует выходной сигнал, пропорциональный их фазовой разности. Этот разностный сигнал есть сигнал ошибки, который характеризует стабильность системы, и в установившемся режиме его значение стремится к нулю. Иначе говоря, система стабильна, когда значение e(s) равно нулю. Следовательно, данная система, а соответственно и система ФАПЧ, является автоматической системой регулирования или следящей системой, а мерой регулирования частоты является разность фаз входного (опорного) сигнала и сигнала цепи обратной связи.
Далее можно сделать следующий вывод: в системе ФАПЧ осуществляется интегрирование; мы измеряем фазу (разность фаз), а регулируем частоту, но фаза является интегралом от частоты.
Рассмотрим теперь стандартную базовую модель ФАПЧ (рис. 2) и входящие в её состав компоненты:
фазовый детектор PD и источник тока CP (Charge Pump);
контурный фильтр, или фильтр нижних частот с передаточной функцией Z(s);
генератор управляемый напряжением VCO (Voltage-Controlled Oscillator);
делитель в цепи обратной связи с коэффициентом деления N.
В фазовом детекторе, как было сказано выше, происходит сравнение двух частотных сигналов и формируется выходной сигнал, пропорциональный их фазовой разности. Когда оба сигнала равны по фазе и частоте, сигнал ошибки будет равен нулю, и контур "замыкается".
Можно привести следующее уравнение, характеризующее значение сигнала ошибки e(s):
e(s) = Fref – (F0/N), (3)
когда e(s) = 0,
Fref = F0/N, (4)
отсюда следует
F0 = N·Fref. (5)
Когда F0 N·Fref, на выходе фазового детектора формируется разностный периодический сигнал, который далее с выхода источника тока подаётся на фильтр нижних частот.
Этот усиленный и отфильтрованный сигнал фазовой ошибки в виде управляющего напряжения, в свою очередь, будет управлять VCO, частота которого будет увеличиваться или уменьшаться по мере необходимости на значение KvV, где Kv - чувствительность VCO в МГц/В и V - изменение напряжения на входе VCO. Это будет продолжаться до тех пор, пока значение e(s) не станет равным нулю и контур заблокируется. Следовательно, VCO преобразует поступающее на него входное напряжение в производную фазы по времени, то есть в частоту. Таким образом, источник тока и генератор управляемый напряжением служат в качестве интегратора, который, обнаруживая сигнал ошибки, регулирует значение выходной частоты таким образом, чтобы значение этой самой ошибки свести к нулю. За счёт интегрирования в контуре регулирования появляется фазовый сдвиг на 90º. Таким образом интегратор, включенный в контур цепи ООС, вносит дополнительное запаздывание по фазе на 90º и на частотах, где коффициент усиления равен единице, может вызывать самовозбуждение. Одно из решений - не включать в контур регулирования компоненты, дающие дополнительное запаздывание по фазе, по крайней мере, на частотах, где коэффициент усиления близок к единице.
Чтобы несколько прояснить ситуацию, вернёмся немного назад. Частотой VCO можно управлять, подавая на его вход соответствующее напряжение. Здесь, казалось бы, можно поступить так же, как и в любом усилителе с обратной связью - ввести контур регулирования с некоторым коэффициентом передачи, как это делается при проектировании схем на операционных усилителях. Но имеется одно важное отличие: в схемах на операционных усилителях регулируемая с помощью обратной связи величина совпадала с величиной, измеряемой с целью формирования сигнала ошибки или была хотя бы пропорциональна ей. Так, например, в усилителях напряжения измеряется выходное напряжение и соответствующим образом подстраивается входное. Несколько иная ситуация для системы ФАПЧ, так как здесь мы измеряем фазу, а регулируем частоту, то есть как было сказано выше, происходит интегрирование, за счёт которого появляется тот самый фазовый сдвиг. Однако необходимо заметить, что операционные усилители имеют запаздывание по фазе на 90º почти на всём своём частотном диапазоне, но при этом хорошо работают.
Чтобы не включать в контур элементы, вносящие дополнительное запаздывание по фазе, можно предложить и проанализировать один из вариантов построения контура регулирования, так называемый "контур первого порядка", при котором в качестве источника тока выступает операционный усилитель, но исключается из схемы фильтр низких частот. При таком построении схемы вход VCO непосредственно связан с выходом источника тока на операционном усилителе, что не позволяет сглаживать помехи и флуктуации входного сигнала, так как данная схема не обладает так называемым свойством "маховика", которое обеспечивается благодаря введению фильтрации по низкой частоте. К тому же, "контур первого порядка" не сохраняет постоянным фазовое соотношение между опорным сигналом и сигналом VCO по той самой причине, что выход источника тока непосредственно соединён со входом VCO. Из всего сказанного выше можно предположить, что "контуры первого порядка" не годятся для построения контуров регулирования цепи ФАПЧ.
Следующий подход - это использование "контура второго порядка", в который вводится дополнительная фильтрация по низкой частоте. Такой контур обладает необходимым свойством "маховика", сглаживая тем самым помехи и флуктуации входного сигнала, к тому же он уменьшает полосу захвата, при попадании в которую частота VCO начинает стабилизироваться системой ФАПЧ. Существует также и полоса удержания, то есть максимальная полоса расстройки VCO, в которой замкнутый контур ФАПЧ стабилизирует частоту VCO. Ширина полос захвата и удержания зависит как раз от вида частотно-фазовой характеристики фильтра нижних частот и общего коэффициента передачи контура регулирования. В правильно спроектированной системе ФАПЧ полоса удержания больше или равна полосе захвата, система стабильна и не самовозбуждается. Здесь необходимо также отметить, что при введении фильтрации по низкой частоте несколько увеличивается и время захвата, которое характеризует скорость вхождения в захват и удержание системы ФАПЧ в режиме слежения при резком изменении частоты. Анализируя сказанное выше, можно сделать вывод, что для системы ФАПЧ подходят "контуры второго порядка", которые обеспечивают малые флуктуации фазы выходного сигнала, а также обладают некоторыми свойствами памяти или "маховика".
Полная передаточная функция для ФАПЧ может быть представлена при помощи выражения GCL для системы отрицательной обратной связи. Здесь вводим дополнительное понятие Forward Gain, обозначенное через G, как коэффициент, характеризующий усиление в прямом направлении, и понятие Loop Gain, обозначенное через GH, как коэффициент передачи контура.
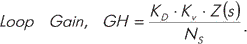 (8)
(8)
Когда величина GH больше единицы, можно говорить, что контур замыкается, и передаточная функция для системы ФАПЧ с коэффициентом деления N имеет вид:
Fout = N x Fref. (9)
Прежде чем приступить к рассмотрению методов синтезирования сигналов, желательно рассмотреть некую несколько отвлеченную модель (рис. 4), показывающую процесс формирования последовательности целочисленного (Integer) потока данных.
Рисунок 4. Модель, отображающая процесс формирования потока данных
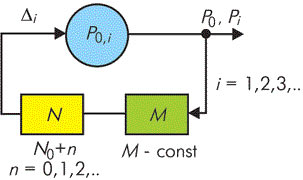
На рис. 4 обозначены:
P0,i - последовательность выходных данных; предполагается, что при запуске системы на выходе присутствует какое-то первоначальное фиксированное значение;
M - делитель с постоянным коэффициентом деления;
N - делитель с переменным коэффициентом деления;
i - приращение к значению последовательности выходных данных, должно быть постоянным для обеспечения стабильности системы.
При первоначальном запуске системы, то есть при i = 1 и n = 0, P0 будет иметь какое-то фиксированное значение, которое "пройдя" через делители M и N, даст нам значение 1. На первом шаге к значению делителя N ничего не прибавлялось, так как при i = 1 n = 0. На втором шаге, при i = 2 и n = 1, мы увеличиваем значение делителя N на n и так далее. Непременным условием является постоянное значение на всех шагах цикла. Казалось бы, всё просто и понятно, но анализируя весь процесс, можно вывести следующие выражения, которые могут пригодиться в анализе работы реальных синтезаторов.
Певоначальное зачение 1 можно получить из выражения:
(10)
Последовательность значений ![]() i (начиная с
i (начиная с ![]() 2) получим из выражения:
2) получим из выражения:
(11)
или, несколько упростив, получим:
(12)
Выражение в скобках (i-1)n говорит о том, что предыдущее значение стабильной системы (система стабильна при i = const) должно быть умножено на значение n для нового шага, и n прибавляется к значению N (в знаменателе). Другими словами, для получения i = const и тем самым обеспечения стабильности системы мы должны с каждым новым шагом увеличивать n на единицу. Справедливости ради необходимо заметить, что мы пошли от обратного, так как в реальных синтезаторах изменением значения переменного коэффициента деления мы изменяем выходную частоту таким образом, чтобы при заданных значениях M и N автоматически (после деления) получить уже заданное ранее значение .
Значение Pi можно представить как
Pi = P0 + i(n+1) (13)
или
Pi = Pi-1 + 1 . (14)
Выражения (12) и (14) показывают взаимосвязь между значениями коэффициентов деления делителей M и N, первоначальным значением системы P0, его последующем увеличением и значением приращения. Взяв какое-либо целое число в качестве P0 и проделав несложные математические операции (задав соответственно значения делителей M и N так, чтобы деление было без остатка), по приведённым выше формулам (10), (12) и (14) получим значения 1 и P1, 2 и P2, 3 и P3 и так далее.
Литература
Curtin M., O’Brien P. Phase-Locked Loops for High-Frequency Receivers and Transmitters. Part 1. Analog Dialogue - 3. 1999.
Horowitz P., Hill W. The Art of Electronics. Second Edition. Cambridge University Press. 1989.