Кузнецов Д.Н. ассистент

Источник: Зб.наук.пр. ДонНТУ. Серія: Обчислювальна техніка та автомати-зація. Випуск 58: – Донецьк: Вид-во ДонНТУ. – 2003. – С.75-80

Аннотация

Выполнено исследование погрешностей определения скорости газа по методу измерения динамического давления. Выявлен критический режим градуировки, при котором суммарная погрешность максимальна. Установлена зависимость, между допустимой погрешностью измерения температуры газа и погрешностью измерения динамического давления, при которых суммарная погрешность измерения скорости газа не превышает установленного предела.

Постановка задачи исследований.

Для увеличения точности и эффективности градуировок термоанемометров в СКТБ “Турбулентность ” при Донецком нацианальном университете была разработана ИИС автоматизации и контроля градуировок ТА [1, 2]. В состав ИИС входят следующие основные измерительные каналы:

1. канал измерения динамического давления;
2. канал измерения температуры образцовым термометром;
3. канал измерения выходного напряжения термоанемометра;
4. канал измерения температуры термометром, встроенным в ТА.

Градуировка осуществляется на аэродинамической установке АДС-200/250 путем сопоставления данных измерений ТА с данными, полученными от образцового средства измерения скорости газа. В качестве образцового средства измерения (ОСИ) скорости газа используется трубка Пито. При этом скорость газа определяется, согласно ГОСТ 17.2.4.06–90, по методу измерения динамического давления газа (Рд)

Рд=Рп – Рст,                                                                      (1)

где Рп – полное давление газа, Па, Рст – статическое давление газа, Па;

и последующего расчета скорости газа по формуле

,                                                                     (2)

где 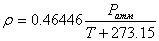 – плотность газа при рабочих условиях, кг/м3, Ратм – атмосферное давление, Па, Т – температура газа, °С.

При расчете градуировочных зависимостей целесообразно оперировать критериальными соотношениями, что в дальнейшем даст возможность проводить измерения в газах иного состава, используя результаты градуировки на воздухе. Число Рейнольдса для трубки Пито

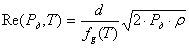,                                                        (3)

где d – диамитр измерительного отверстия трубки, – динамическая вязкость газа.

При проектировании измерительных каналов ИИС градуировки ТА возникла необходимость в  оценке погрешностей образцового средства измерения скорости газа при различных скоростях и температурах газового потока, с целью выявления критической области измерений, в которой погрешность максимальна.

Оценка погрешностей определения скорости газа.

Из (3) следует, что число Рейнольдса определяется косвенным путем и для его расчета необходимо выполнить прямые измерения динамического давления и температуры газа. Доверительная граница неисключенной систематической погрешности измерения числа Рейнольдса трубкой Пито [3]:

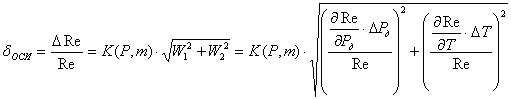,                (4)

где W1, W2 – частные относительные погрешности измерения числа Re, обусловленные погрешностями прямых измерений динамического давления и температуры газа соответственно; DРд, DТ – абсолютные погрешности измерений разности давлений и температуры газа; K – коэффициент, обусловленный принятой доверительной вероятностью Р и числом m составляющих dосн (при Р=0,95 К=1,1 и мало зависит от m).

Найдем частные производные (весовые функции), входящие в (4):

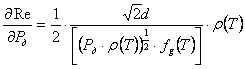;                                              (5)

.                         (6)

Исследуем частные погрешности W1 и W2, определим характер их изменения во всем диапазоне скоростей и температур градуировки и выделим критические области, в которых погрешности максимальны. Вычисления осуществим в пакете MathCad.  На рис.1 представлены графики зависимости частной погрешности W1 от числа Re (от скорости) при граничных температурах градуировки и DPд=1 Па. Из результатов приведенных на рисунке следует, что погрешность W1 возрастает с уменьшением скорости потока и его температуры. Таким образом, критическим режимом для W1 является режим с минимальными скоростью и температурой потока. На рис.2 представлены результаты исследования частной погрешности W2 при DТ=1°С, которые показывают, что W2 не зависит от скорости газа и возрастает с уменьшением его температуры. Критический режим для W2 – минимальная температура градуировки.

На основании результатов исследований частных погрешностей W1, W2  делаем вывод, что ОСИ  дает максимальную погрешность измерений при минимальной скорости и температуре воздушного потока.

Рисунок 1 – Зависимость W1 от Re при граничных значениях температуры газа.

Рисунок 2 – Зависимость W2 от Re при граничных значениях температуры газа.

Выполним исследование суммарной погрешности ОСИ скорости газа для выявленного критического режима с минимальной скоростью и температурой потока (Re=500 и Т=0 °C). Погрешность ОСИ по техническому заданию (ТЗ) не должна  превышать 0,5%. Проанализируем полученные результаты. На рис.3 представлены графики зависимости суммарной относительной погрешности ОСИ dОСИ от абсолютной погрешности измерения динамического давления DРд при различных значениях абсолютной погрешности измерения температуры газа DТ.

Рисунок 3 – Зависимость суммарной погрешности ОСИ от погрешности измерения температуры газа при различных значениях DРд.

Рисунок 4 – Зависимость суммарной погрешности ОСИ от погрешности измерения динамического давления при различных значениях DТ.

Рисунок 4 содержит аналогичные результаты, но полученные для случая, когда  DТ является непрерывным аргументом, а DР – дискретным.

Из результатов исследований следует, что с уменьшением погрешности измерения давления, растет предел допустимой погрешности по температуре и наоборот, чем выше класс точности термометра, тем менее точный нужен дифманометр.

Установим связь между допустимой погрешностью термометра и погрешностью дифманометра, обеспечивающие заданное значение суммарной погрешности ОСИ. Для этого перепишем выражение (4) относительно DТ:

.                                                (7)

Графическая интерпретация  зависимости (7) представлена на рис.5.

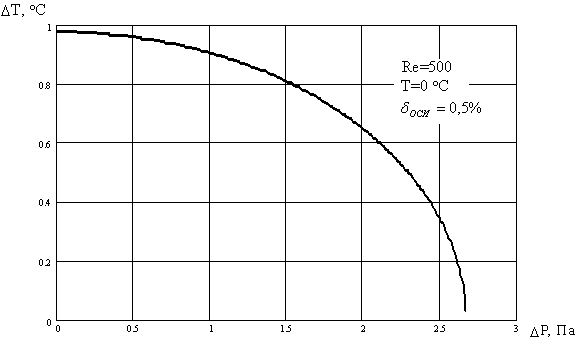
Рисунок 5 – Зависимость погрешности измерения температуры газа от погрешности измерения динамического давления, обеспечивающие заданное значение суммарной погрешности ОСИ (dОСИ=0,5 %).

Анализ результатов показывает, что при DРд<1,5Па допустимый уровень DТ слабо зависит от DРд и находится в пределах от 0,8 до 1 °С. Однако с увеличением DРд от 2 Па и выше требования к точности измерения температуры газа резко возрастают и при DРд=2,5 Па   предел допустимой погрешности по температуре составляет всего 0,35 °С. Полученная зависимость позволяет по заданной суммарной погрешности ОСИ скорости газа поставить требования к точности измерительных каналов температуры газа и динамического давления.

Выводы

1. На основании результатов исследований погрешностей измерения скорости газа по методу измерения динамического давления при помощи трубки Пито выявлен критический режим градуировки, при котором суммарная погрешность максимальна. Это режим с минимальными скоростью и температурой газа.
2. Установлена зависимость, между допустимой погрешностью измерения температуры газа и погрешностью измерения динамического давления, при которых суммарная погрешность измерения числа Рейнольдса не превышает установленного предела. Полученная зависимость позволяет по заданной суммарной погрешности ОСИ скорости газа поставить требования к точности измерительных каналов температуры газа и динамического давления.

Литература

1. Зорi А.А., Украiнський Ю.Д., Кузнецов Д.M. Cистема автоматизації градуювання первинних вимірювальних перетворювачів термоанемометрів. Науковi працi Донецького державного технiчного унiверситету. Серiя: Обчислювальна технiка та автоматизацiя, випуск 20: – Донецьк: ДонДТУ, 2000.– с. 260-268.
2. Зори А.А., Кузнецов Д.Н. Повышение эффективности градуировки первичных измерительных преобразователей термоанемометров. Серiя: Обчислювальна технiка та автоматизацiя, випуск 25: – Донецьк: ДонДТУ, 2001.– с. 183-189.
3. Селиванов М.Н., Фридман А.Э., Кудряшова Ж.Ф. Качество измерений: Метрологическая справочная книга. – Л.: Лениздат, 1987. – 295 с., ил.
4. Зори А.А., Коренев В.Д., Хламов М.Г. Методы, средства, системы измерения и контроля параметров водных сред. – Донецк: РИА ДонГТУ, 2000. – 388 с.: ил.
5. Ярин Л.П. и др. Термоанемометрия газовых потоков/ Л.П.Ярин, А.Л.Генкин, В.И.Кукес. –Л.: Машиностроение, Ленингр. отд-ние, 1983, – 198 с., ил.