
Цыбулька Владимир Сергеевич
Алгоритм опроса измерительного канала средней скорости потока аэродинамического стенда, инвариантный к уровню его турбулентности
Кузнецов Д.Н.
Источник: Зб.наук.пр. ДонНТУ. Серія: Обчислювальна техніка та автоматизація. Випуск 90: – Донецьк: ДонНТУ, – 2005.– С.193-198
Abstract
The algorithm ensuring invariancy a casual error of measurements average speed of a flow from a level pulsations of instant speed is considered.
Общая постановка проблемы.
В СКТБ «Турбулентность» при Донецком национальном университете совместно с кафедрой «Электронная техника» Донецкого национального технического университета разработана специализированная информационно-измерительная система (ИИС) градуировки термоанемометрических измерительных преобразователей скорости (ТИПС) газа повышенной эффективности с использованием аэродинамического стенда АДС-200/250 [1,2]. Одним из способов повышения эффективности градуировки ТИПС, является снижение продолжительности градуировки путем сокращения времени многократного опроса измерительных каналов ИИС.
Постановка задачи.
Многократный опрос каналов ИИС осуществляется с целью повышения точности и достоверности измерительных данных градуировки путем их статистической обработки. Длительность этой операции прямо пропорциональна объему выборки, который, в свою очередь, определяется требованиями к точности результатов измерений и уровнем турбулентности потока. Известно, что объем выборки пропорционален дисперсии сигнала [3], т.е. при увеличении (уменьшении) среднего уровня пульсаций скорости в М раз объем выборки и время измерений необходимо увеличить (уменьшить) в М2 раз. Установили, что уровень турбулентности потока в АДС в общем случае не постоянен и зависит от ряда факторов, в том числе от скорости потока. Эксперименты подтвердили, что на малых скоростях (порядка 1 м/с) относительный уровень пульсаций мгновенной скорости потока в 4…5 раз больше, чем на максимальной (40 м/с). Следовательно, необходимый объем выборки в различных режимах и точках градуировки будет разным. При меньших объемах выборок не выполняются требования по точности измерений, а при больших – имеет место неоправданное уменьшение быстродействия.
Решение задачи и результаты исследований.
Сущность предложенного алгоритма опроса и первичной обработки данных измерительных каналов ИИС градуировки, инвариантного к уровню пульсаций скорости потока, заключается в итеративном определении, непосредственно в процессе многократного опроса каналов, минимального количества выборок мгновенных значений измерительных сигналов, достаточного для минимизации случайной составляющей суммарной погрешности результата измерения средней скорости до уровня, позволяющего пренебречь ею в сравнении с неисключенной систематической составляющей.
Условие, при котором случайной погрешностью измерений можно пренебречь, определяется неравенством [4]:
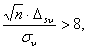 (1)
(1)
где n – объем выборки; Dsv и sv – соответственно неисключенная систематическая погрешность (НСП) и СКО случайной погрешности результатов наблюдений скорости потока.
Откуда, минимальное достаточное количество наблюдений:
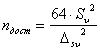 . (2)
. (2)
Предложенных алгоритм многократного опроса и обработки данных измерительных каналов ИИС градуировки, инвариантный к уровню турбулентности потока, состоит из следующих шагов:
- Определить минимальный объем выборки мгновенных значений сигнала измерительного канала средней скорости потока, обеспечивающий требуемую достоверность статистических оценок [4], по формуле:
 . (3)
. (3) - Выполнить опрос выбранного канала nmin раз и сформировать выборку минимального объема.
- Исключить из полученного ряда наблюдений результаты, содержащие грубые погрешности.
- Если условие (1) выполняется, то переход на п.5, иначе выполнить однократный опрос выбранного канала и перейти на п.3.
- За результат измерения принять среднее арифметическое ряда наблюдений.
Предложенный алгоритм обеспечивает инвариантность (независимость) точности измерений средней скорости потока от уровня его турбулентности.
Блок-схема предложенного алгоритма приведена на рис.1.
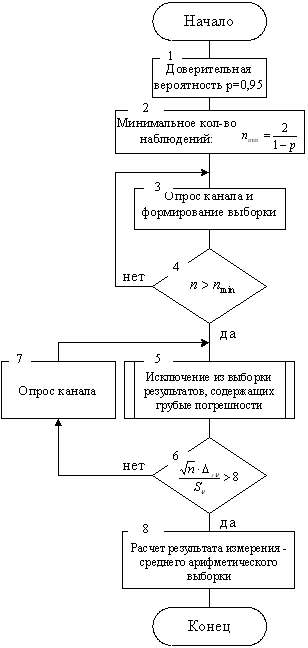
Рис.1. Блок схема алгоритма опроса измерительного канала средней скорости потока ИИС градуировки, инвариантный к уровню его турбулентности
Выполним оценку сокращения времени операции многократного опроса измерительных каналов ИИС. В качестве исходных данных примем следующие: интервал временной дискретизации То=0,1 с, допустимая НСП результата измерения средней скорости потока Dsv=0,5 %, зависимость уровня турбулентности потока в области градуировки от средней скорости, полученная экспериментально (рис.2).
Результаты расчета объемов выборок n и длительностей измерений Т в различных точках по скорости потока сведены в табл.1.
Табл.1. Результаты расчета объемов выборок n и длительностей измерений Т в различных точках по скорости потока
i | ui, кг/м2/с |
sui, % |
ni |
Ti, c |
1 |
1 |
2,2 |
1239 |
123,9 |
2 |
2 |
2 |
1024 |
102,4 |
3 |
4 |
1,6 |
655 |
65,5 |
4 |
6 |
1,45 |
538 |
53,8 |
5 |
9 |
1,2 |
369 |
36,9 |
6 |
15 |
1 |
256 |
25,6 |
7 |
20 |
0,85 |
185 |
18,5 |
8 |
25 |
0,8 |
164 |
16,4 |
9 |
30 |
0,75 |
144 |
14,4 |
10 |
40 |
0,7 |
125 |
12,5 |
На основании полученных результатов определим:
- Суммарное время измерений при использовании предложенного алгоритма опроса каналов:
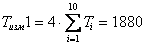 с. (4)
с. (4) - Суммарное время измерений без использования предложенного алгоритма опроса каналов:
 с. (5)
с. (5)
Используем полученных выше результаты для оценки сокращения времени измерений при градуировке от использования алгоритма опроса каналов, инвариантного к уровню пульсаций скорости потока:
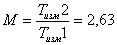 . (6)
. (6)
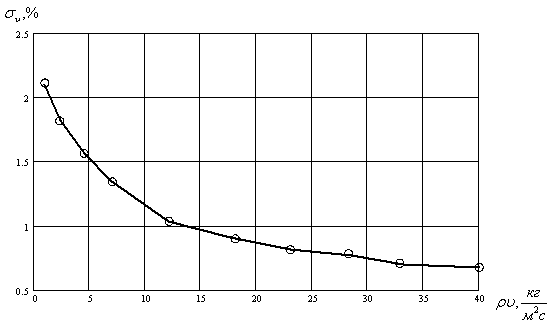
Рис.2. Зависимость уровня турбулентности потока в АС от средней скорости
С целью повышения достоверности измерительных данных предложенный алгоритм содержит процедуру исключения из выборки результатов наблюдений, которые содержат грубые погрешности (блок 5 на рис.1).
Грубыми называют погрешности, которые существенно превышают ожидаемые в данных условиях измерений [3]. Между результатами, содержащими грубые погрешности, и результатами, которые заслуживают доверия, часто нельзя провести четкую границу. В этом случае вопрос о том, содержит ли данный результат измерений грубую погрешность, решается одним из методов проверки статистических гипотез. При выявлении грубых погрешностей проверяемая гипотеза допускает, что результат измерений хi не содержит грубой погрешности и является одним из значений случайной величины Х. Сомнения в первую очередь вызывают наибольший (xmax) и наименьший (xmin) из результатов наблюдений. Блок-схема алгоритма исключения результатов измерений, содержащих грубые погрешности, представлена на рис.3. Проверка гипотезы сводится к следующему:
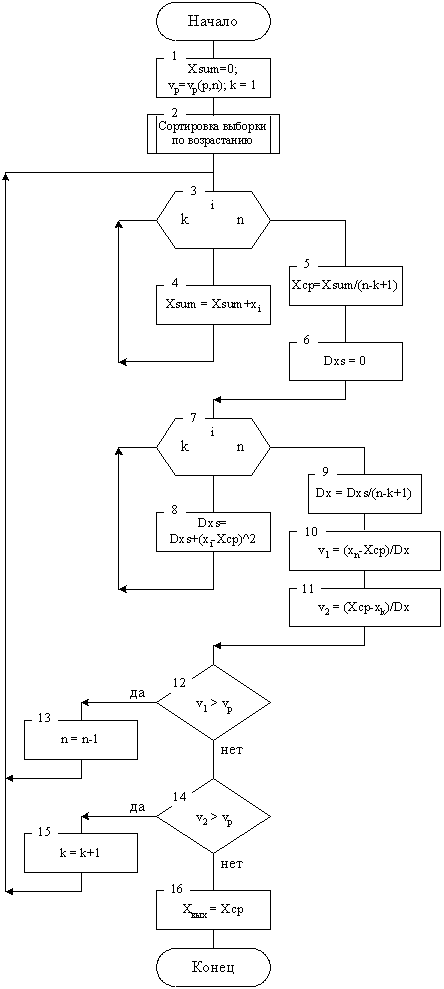
Рис.3 Блок-схема алгоритма исключения результатов измерений, содержащих грубые погрешности
- для полученного ряда наблюдений находят статистические оценки параметров нормального закона распределения вероятностей – математического ожидания и дисперсии
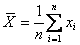 ; (7)
; (7)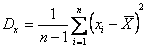 . (8)
. (8) - находят вспомогательные отношения
 ; (9)
; (9)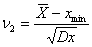 . (10)
. (10) - по справочным данным по заданной доверительной вероятности Р и числу результатов наблюдений n находят наибольшее значение nр, которая случайная величина n может принять еще с чисто случайных причин.
- если рассчитанное значение n1 (или n2) окажется меньше nр, то гипотеза принимается; в противном случае результат xmax (или xmin) исключается из ряда наблюдений и вновь полученный ряд проверяется на наличие грубых погрешностей по методике, изложенной выше.
Выводы.
Предложенный алгоритм опроса измерительных каналов ИИС градуировки ТИПС обеспечивает:
- Инвариантность случайной погрешности измерений средней скорости потока от уровня его турбулентности.
- Заданную достоверность результатов измерений средней скорости потока.
- Сокращение времени измерений в 2,6 раза.
Литература
- Зорi А.А., Украiнсьий Ю.Д., Кузнецов Д.M. Cистема автоматизації градуювання первинних вимірювальних перетворювачів термоанемометрів. Науковi працi Донецького державного технiчного унiверситету. Серiя: Обчислювальна технiка та автоматизацiя, випуск 20: – Донецьк: ДонДТУ, 2000.– с. 260-268.
- Зори А.А., Кузнецов Д.Н. Методы и программно-аппаратные средства автоматизированной системы градуировки первичных измерительных преобразователей термоанемометров. Известия ТРТУ. Тематический выпуск: Материалы Всероссийской научно-технической конференции с международным участием "Компьютерные технологии в инженерной и управленческой деятельности". Таганрог: ТРТУ, 2002, №2 (25). – с.148-150.
- Селиванов М.Н., Фридман А.Э., Кудряшова Ж.Ф. Качество измерений: Метрологическая справочная книга. – Л.: Лениздат, 1987. – 295 с., ил.
- ГОСТ 8.207–76. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений.