Библиотека

Источник: http://www.gmdh.net/articles/theory/TimeSeries.pdf

Грешилов А.А., Стакун В.А., Стакун А.А.

“Математические методы построения прогнозов”

ВВЕДЕНИЕ

Процедуры построения прогнозов используются практически во всех областях знания, в том числе в экономике, социологии, технике, образовании и т. д. Процесс построения прогноза можно представить в виде двух взаимно связанных задач:

1) построение модели исследуемого явления;

2) оценка основных характеристик (параметров) модели по базовым данным и получение по этой модели интервальной оценки прогноза.

Как правило, эти задачи дополняют одна другую, процесс построения прогноза часто бывает итерационным - оценка параметров модели по базовым данным и полученные интервальные оценки прогноза могут послужить основанием для изменения исходной модели и последующего пересчета прогноза. В задаче расчета прогноза особое внимание должно быть уделено учету погрешностей исходных данных при оценке характеристик (параметров) модели и процедуре получения интервальных оценок прогнозов.

Первая задача базируется на физических законах, законах развития общества, а часто на интуиции, тогда как вторая задача может быть решена методами математической статистики. Таким образом, если из законов природы и общественного развития может быть получена модель явления, то основная проблема переносится на математические методы построения прогноза.

В процессе построения модели явления опираются, как правило, на наиболее устойчивые события. Например, наилучшее условие для построения модели и последующего прогноза - когда процесс или параметры модели постоянны. Поэтому при построении модели наряду с интегральными методами и элементарными функциями пользуются конечными разностями такого порядка, при которых процесс считается стационарным.

Системы называются стационарными, если их динамические свойства не изменяются с течением времени; если такое изменение имеет место, то системы называют нестационарными. Стационарность означает, что процесс преобразования входных возмущений системой обладает свойством инвариантности относительно сдвига во времени входных возмущений.

Модели бывают концептуальные, физические или математические (другие названия: феноменологические, эмпирические и аналитические) в зависимости от того, какая сторона явления в данном случае наиболее существенна, от методов, которые можно использовать при построении модели, от количества и качества имеющейся информации.

Относительная простота является главной характеристикой модели. Во многих случаях для того, чтобы модель была полезной, ее сложность должна находиться в определенном соотношении со сложностью описываемого объекта. Если физический механизм явления полностью ясен, можно вывести математическое выражение, точно описывающее явление. Во многих случаях для получения таких описаний (моделей) нужны подробные сведения, которых может не быть, и приходится прибегать к эмпирической модели. Оба названных случая представляют собой крайности. Обычно используемые модели занимают промежуточное положение. В частности, можно использовать неполные теоретические представления для указания подходящего класса математических функций, которые могут быть затем эмпирически подогнаны, когда число параметров модели и их числовые значения оцениваются по экспериментальным данным.

При подгонке моделей теоретический анализ не только указывает на подходящий вид модели, но может дать хорошие оценки числовых значений ее параметров. Эти значения затем можно проверить, анализируя реальные данные. Результат такой проверки служит в свою очередь основанием для пересмотра модели. Итерационный подход к построению моделей включает в себя следующие этапы:

1. На основе теории и практики явления выбирается класс моделей, ориентируясь на те цели, для которых создается модель.

2. Разрабатываются простейшие методы идентификации подклассов этих моделей. Процесс идентификации может быть использован для получения грубых предварительных оценок параметров моделей.

3. Пробная модель подгоняется к экспериментальным данным; оцениваются ее параметры. Грубые оценки, полученные на этапе идентификации, теперь можно использовать как начальные значения в более точных итеративных методах оценивания параметров.

4. Диагностические проверки позволяют выявить возможные дефекты подгонки и диагностировать их причины. Если такие дефекты не выявлены, модель готова к использованию. Если обнаружено какое-либо несоответствие, итеративные циклы идентификации, оценок и диагностической проверки повторяются до тех пор, пока не будет найдено подходящее представление модели.

В практике широко применяются параметрические модели, что повысило интерес к задачам оценивания параметров и к родственным вопросам при построении таких моделей по экспериментальным данным. При построении модели надо стремиться ответить на следующие вопросы:

1) как оценить качество модели;

2) как учесть всю имеющуюся информацию;

3) в чем состоит оптимальная стратегия получения недостающей информации;

4) как поступить с нелинейностями;

5) можно ли аппроксимировать сложную систему простой моделью.

Ответы на эти вопросы зависят от конкретного класса систем. На практике отыскание подходящей модели может быть достаточно трудной задачей.

Математическую модель системы называют детерминированной, если входящие в нее описания воздействия и параметры модели являются постоянными или детерминированными функциями переменных состояния и времени. Математическую модель системы называют статистической (стохастической), если функции, описывающие воздействия и параметры модели, являются случайными функциями или случайными величинами. Для стохастических (вероятностных) динамических систем текущее состояние в момент t₁-X(t₁) и входное воздействие w = w(t₁, t₂) определяют в момент t₂ не X(t₂), а лишь его вероятностное распределение.

Модели временных рядов и исследуемых процессов, необходимые для получения оптимального прогнозирования, в действительности являются стохастическими, поскольку на изучаемый процесс действует большое число неизвестных факторов и нельзя предложить детерминированную модель, допускающую точное вычисление будущего поведения объекта. Можно вычислить вероятность того, что некоторое будущее значение будет принадлежать определенному интервалу. В дальнейшем будем различать вероятностную модель или стохастический процесс и наблюдаемый временной (вариационный) ряд z₁, z₂, :, z_N, который рассматривается как выборочная реализация.

Важный класс стохастических процессов, рассматриваемых в приложениях,- стационарные процессы. Полезным инструментом для описания поведения стационарных процессов является автокорреляционная функция. Ковариация между значениями z_t и z_t+k одного вариационного (временного) ряда, отделенными k интервалами времени, называется автоковариацией с задержкой k и определяется как

Автокорреляция с задержкой k равна

,

где σ_z² = γ₀; γ_k = ρ_kσ_z²

Функция γ_k от задержки k называется автоковариационной функцией {γ_k} стохастического процесса; функция ρ_k от задержки k называется автокорреляционной функцией {ρ_k} стохастического процесса. На практике определяют только выборочные оценки этих функций. Так оценка ρ_k : ,

где 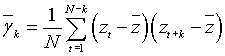; k = 0, ..., m, N - число наблюдений, z - среднее значение ряда наблюдений. Дисперсия выборочного ряда наблюдений

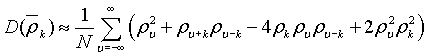
Если ρ_k = Ф^|k|(-1 < Ф < 1) - затухает экспотенциально, то

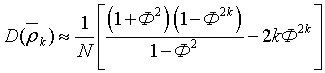
Но многие встречающиеся на практике временные ряды имеют нестационарные характеристики. В книге рассмотрен класс нестационарных моделей, называемый моделями авторегрессии - проинтегрированного скользящего среднего (АРПСС).

В данной книге рассматриваются стохастические системы, для которых могут быть получены параметрические модели в виде элементарных функций, систем алгебраических уравнений и конечно-разностных описаний интегральных и дифференциальных уравнений. Предполагается, что исследователь располагает только случайными исходными данными: случайными будут входное воздействие и выход системы, или входное воздействие и параметры системы, случайны соответствующие элементы матриц алгебраических уравнений или ядер интегральных уравнений.

Оцениваемые параметры предполагаются либо неизвестными детерминированными величинами и в процессе решения находится доверительный интервал с определенной вероятностью накрывающий неизвестную величину (подход максимального правдоподобия) или случайными величинами с априорно известным законом распределения (байесовский подход).

В первых главах книги описывается необходимый математический аппарат, применяемый при построении прогнозов, и рассматриваются особенности его применения. Затем излагаются собственно процедуры прогнозирования.

В первой главе рассматривается регрессионный анализ и метод наименьших квадратов как инструмент для построения прогнозов; подчеркивается, что погрешность аргумента должна быть много меньше, чем погрешность функции. Здесь же рассматривается "регрессионный парадокс" - явление связанное тем, что из-за наличия погрешности в наблюдаемых величинах, по одним и тем же исходным данным, меняя местами аргументы и функции (зависимые и независимые переменные), получим заметно различающиеся прогнозы.

Во второй главе даются методы математической статистики которые позволяют учитывать в процессе построения прогнозов одновременно погрешности и в значениях функции, и в значениях аргументов - конфлюентный анализ. Эти алгоритмы исключают "регрессионный парадокс". Рассмотрены алгоритмы оценки свободных параметров для практически значимых в задачах построения прогнозов элементарных функций.

В третьей главе рассмотрены разностные методы построения прогнозов, экспоненциальное сглаживание и сглаживание с помощью скользящей средней, прогнозирование сезонных явлений; диагностическая проверка моделей и оценка ошибки прогноза. Приводятся алгоритмы подправления прогнозов.

Книга рассчитана на специалистов, занимающимися задачами построения прогнозов, на студентов вузов и на слушателей системы дополнительного профессионального образования, изучающих методы прогнозирования.

 

Источник: http://www.gmdh.net/articles/theory/TimeSeries.pdf