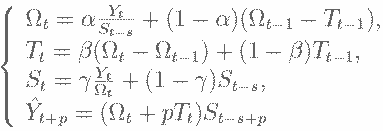Источник: http://www.neuroproject.ru/forecasting_tutorial.php
Введение
Методы прогнозирования, основанные на сглаживании, экспоненциальном сглаживании и скользящем среднем
Регрессионные методы прогнозирования
Методы Бокса-Дженкинса (aRiMa)
Нейросетевые модели бизнес-прогнозирования
Введение
До недавнего времени (середины 80-х годов прошлого века) существовало несколько общепризнанных методов прогнозирования временных рядов:
- Эконометрические
- Регрессионные
- Методы Бокса-Дженкинса (aRiMa, aRMa)
Однако, начиная с конца 80-х годов, в научной литературе был опубликован ряд статей по нейросетевой тематике, в которых был приведен эффективный алгоритм обучения нейронных сетей и доказана возможность их использования для самого широкого круга задач.
Эти статьи возродили интерес к нейросетям в научном сообществе и последние очень скоро стали широко использоваться при исследованиях в самых разных областях науки от экспериментальной физики и химии до экономики.
Кстати, некоторые сотрудники компании "Нейропроект" начали заниматься нейронными сетями именно в то время, используя их для обработки результатов физических экспериментов.
Отчасти из-за относительной сложности и недетерминированности
нейронных сетей и генетических алгоритмов, эти технологии не сразу вышли за
рамки чисто научного применения. Тем не менее, с течением времени уровень
доверия к новым технологиям повышался и со стороны бизнеса. С начала 90-х годов
начали регулярно появляться сообщения об установках нейросетевых систем в
разных компаниях, банках, корпоративных институтах. Причем сфера использования
новых технологий была очень многогранной - оценка рисков, контроль
технологических процессов, управлние роботами и многое другое.
Одним из самых успешных приложений нейронных сетей было прогнозирование
временных рядов. Причем самым массовым было
- Прогнозирование на финансовых рынках
- Прогнозирование продаж
В настоящее время можно с уверенностью сказать, что использование нейронных
сетей при прогнозировании дает ощутимое преимущество по сравнению с более
простыми статистическими методами.
Методы прогнозирования, основанные на сглаживании, экспоненциальном сглаживании и скользящем среднем
"Наивные" модели прогнозирования
При создании "наивных" моделей предполагается, что некоторый последний период прогнозируемого временного ряда лучше всего описывает будущее этого прогнозируемого ряда, поэтому в этих моделях прогноз, как правило, является очень простой функцией от значений прогнозируемой переменной в недалеком прошлом.
Самой простой моделью является
Y(t+1)=Y(t),
что соответствует предположению, что "завтра будет как сегодня".
Вне всякого сомнения, от такой примитивной модели не стоит ждать большой точности. Она не только не учитывает механизмы, определяющие прогнозируемые данные (этот серьезный недостаток вообще свойственен многим статистическим методам прогнозирования), но и не защищена от случайных флуктуаций, она не учитывает сезонные колебания и тренды. Впрочем, можно строить "наивные" модели несколько по-другому
Y(t+1)=Y(t)+[Y(t)-Y(t-1)],
Y(t+1)=Y(t)*[Y(t)/Y(t-1)],
такими способами мы пытаемся приспособить модель к возможным трендам
Y(t+1)=Y(t-s),
это попытка учесть сезонные колебания
Средние и скользящие средние
Самой простой моделью, основанной на простом усреднении является
Y(t+1)=(1/(t))*[Y(t)+Y(t-1)+...+Y(1)],
и в отличии от самой простой "наивной" модели, которой соответствовал принцип "завтра будет как сегодня", этой модели соответствует принцип "завтра будет как было в среднем за последнее время". Такая модель, конечно более устойчива к флуктуациям, поскольку в ней сглаживаются случайные выбросы относительно среднего. Несмотря на это, этот метод идеологически настолько же примитивен как и "наивные" модели и ему свойственны почти те же самые недостатки.
В приведенной выше формуле предполагалось, что ряд усредняется по достаточно длительному интервалу времени. Однако как правило, значения временного ряда из недалекого прошлого лучше описывают прогноз, чем более старые значения этого же ряда. Тогда можно использовать для прогнозирования скользящее среднее
Y(t+1)=(1/(T+1))*[Y(t)+Y(t-1)+...+Y(t-T)],
Смысл его заключается в том, что модель видит только ближайшее прошлое (на T отсчетов по времени в глубину) и основываясь только на этих данных строит прогноз.
При прогнозировании довольно часто используется метод экспоненциальных средних, который постоянно адаптируется к данным за счет новых значений. Формула, описывающая эту модель записывается как
Y(t+1)=a*Y(t)+(1-a)*^Y(t),
где Y(t+1) – прогноз на следующий период
времени
Y(t) – реальное значение в момент времени t
^Y(t) – прошлый прогноз на момент времени t
a – постоянная сглаживания
(0<=a<=1))
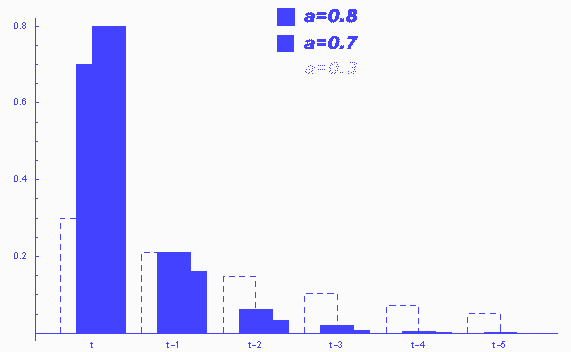
В этом методе есть внутренний параметр a,
который определяет зависимость прогноза от более старых данных, причем влияние
данных на прогноз экспоненциально убывает с "возрастом" данных.
Зависимость влияния данных на прогноз при разных коэффициентах a приведена на графике.
|
|
Видно, что при a->1, экспоненциальная модель стремится к самой простой "наивной" модели. При a->0, прогнозируемая величина становится равной предыдущему прогнозу.
Если производится прогнозирование с использованием модели экспоненциального сглаживания, обычно на некотором тестовом наборе строятся прогнозы при a=[0.01, 0.02, ..., 0.98, 0.99] и отслеживается, при каком a точность прогнозирования выше. Это значение a затем используется при прогнозировании в дальнейшем.
Хотя описанные выше модели ("наивные" алгоритмы, методы, основанные на средних, скользящих средних и экспоненциального сглаживания) используются при бизнес-прогнозировании в не очень сложных ситуациях, например, при прогнозировании продаж на спокойных и устоявшихся западных рынках, мы не рекомендуем использовать эти методы в задачах прогнозирования в виду явной примитивности и неадекватности моделей.
Вместе с этим хотелось бы отметить, что описанные алгоритмы вполне успешно можно использовать как сопутствующие и вспомогательные для предобработки данных в задачах прогнозирования. Например, для прогнозирования продаж в большинстве случаев необходимо проводить декомпозицию временных рядов (т.е. выделять отдельно тренд, сезонную и нерегулярную составляющие). Одним из методов выделения трендовых составляющих является использование экспоненциального сглаживания.
Методы Хольта и Брауна
В середине прошлого века Хольт предложил усовершенствованный метод экспоненциального сглаживания, впоследствии названный его именем. В предложенном алгоритме значения уровня и тренда сглаживаются с помощью экспоненциального сглаживания. Причем параметры сглаживания у них различны.
|
|
Здесь первое уравнение описывает сглаженный
ряд общего уровня.
Второе уравнение служит для оценки тренда.
Третье уравнение определяет прогноз на p
отсчетов по времени вперед.
Постоянные сглаживания в методе Хольта идеологически играют ту же роль, что и постоянная в простом экспоненциальном сглаживании. Подбираются они, например, путем перебора по этим параметрам с каким-то шагом. Можно использовать и менее сложные в смысле количества вычислений алгоритмы. Главное, что всегда можно подобрать такую пару параметров, которая дает большую точность модели на тестовом наборе и затем использовать эту пару параметров при реальном прогнозировании.
Частным случаем метода Хольта является метод Брауна, когда a=ß.
Метод Винтерса
Хотя описанный выше метод Хольта (метод двухпараметрического экспоненциального сглаживания) и не является совсем простым (относительно "наивных" моделей и моделей, основанных на усреднении), он не позволяет учитывать сезонные колебания при прогнозировании. Говоря более аккуратно, этот метод не может их "видеть" в предыстории. Существует расширение метода Хольта до трехпараметрического экспоненциального сглаживания. Этот алгоритм называется методом Винтерса. При этом делается попытка учесть сезонные составляющие в данных. Система уравнений, описывающих метод Винтерса выглядит следующим образом:
|
|
Дробь в первом уравнении служит для исключения сезонности из Y(t). После исключения сезонности алгоритм работает с "чистыми" данными, в которых нет сезонных колебаний. Появляются они уже в самом финальном прогнозе, когда "чистый" прогноз, посчитанный почти по методу Хольта умножается на сезонный коэффициент.
Регрессионные методы прогнозирования
Наряду с описанными выше методами, основанными на экспоненциальном сглаживании, уже достаточно долгое время для прогнозирования используются регрессионные алгоритмы. Коротко суть алгоритмов такого класса можно описать так.
Существует прогнозируемая переменная Y (зависимая переменная) и отобранный заранее комплект переменных, от которых она зависит - X1, X2, ..., XN (независимые переменные). Природа независимых переменных может быть различной. Например, если предположить, что Y - уровень спроса на некоторый продукт в следующем месяце, то независимыми переменными могут быть уровень спроса на этот же продукт в прошлый и позапрошлый месяцы, затраты на рекламу, уровень платежеспособности населения, экономическая обстановка, деятельность конкурентов и многое другое. Главное - уметь формализовать все внешние факторы, от которых может зависеть уровень спроса в числовую форму.
Модель множественной регрессии в общем случае описывается выражением
![]()
В более простом варианте линейной регрессионной модели
зависимость зависимой переменной от независимых имеет вид: ![]()
Здесь ![]() -
подбираемые коэффициенты регрессии,
-
подбираемые коэффициенты регрессии,
![]() - компонента ошибки.
Предполагается, что все ошибки независимы и нормально распределены.
- компонента ошибки.
Предполагается, что все ошибки независимы и нормально распределены.
Для построения регрессионных моделей необходимо иметь базу данных наблюдений примерно такого вида:
|
|
переменные |
||||
|
|
независимые |
зависимая |
|||
|
№ |
X1 |
X2 |
... |
XN |
Y |
|
1 |
x_11 |
x_12 |
... |
x_1N |
Y_1 |
|
2 |
x_21 |
x_22 |
... |
x_2N |
Y_2 |
|
... |
... |
... |
... |
... |
... |
|
m |
x_M1 |
x_M2 |
... |
x_MN |
Y_m |
С помощью таблицы значений прошлых наблюдений можно подобрать (например, методом наименьших квадратов) коэффициенты регрессии, настроив тем самым модель.
При работе с регрессией надо соблюдать определенную осторожность и обязательно проверить на адекватность найденные модели. Существуют разные способы такой проверки. Обязательным является статистический анализ остатков, тест Дарбина-Уотсона. Полезно, как и в случае с нейронными сетями, иметь независимый набор примеров, на которых можно проверить качество работы модели.
Методы Бокса-Дженкинса (aRiMa)
В середине 90-х годов прошлого века был разработан принципиально новый и достаточно мощный класс алгоритмов для прогнозирования временных рядов. Большую часть работы по исследованию методологии и проверке моделей была проведена двумя статистиками, Г.Е.П. Боксом (G.E.p. box) и Г.М. Дженкинсом (G.M. Jenkins). С тех пор построение подобных моделей и получение на их основе прогнозов иногда называться методами Бокса-Дженкинса. Более подробно иерархию алгоритмов Бокса-Дженкинса мы рассмотрим чуть ниже, пока же отметим, что в это семейство входит несколько алгоритмов, самым известным и используемым из них является алгоритм aRiMa. Он встроен практически в любой специализированный пакет для прогнозирования. В классическом варианте aRiMa не используются независимые переменные. Модели опираются только на информацию, содержащуюся в предыстории прогнозируемых рядов, что ограничивает возможности алгоритма. В настоящее время в научной литературе часто упоминаются варианты моделей aRiMa, позволяющие учитывать независимые переменные. В данном учебнике мы их рассматривать не будем, ограничившись только общеизвестным классическим вариантом. В отличие от рассмотренных ранее методик прогнозирования временных рядов, в методологии aRiMa не предполагается какой-либо четкой модели для прогнозирования данной временной серии. Задается лишь общий класс моделей, описывающих временной ряд и позволяющих как-то выражать текущее значение переменной через ее предыдущие значения. Затем алгоритм, подстраивая внутренние параметры, сам выбирает наиболее подходящую модель прогнозирования. Как уже отмечалось выше, существует целая иерархия моделей Бокса-Дженкинса. Логически ее можно определить так
aR(p)+Ma(q)->aRMa(p,q)->aRMa(p,q)(p,Q)->aRiMa(p,q,r)(p,Q,R)->...
aR(p) -авторегрессионая модель порядка p.
Модель имеет вид:
Y(t)=f_0+f_1*Y(t-1)+f_2*Y(t-2)+...+f_p*Y(t-p)+E(t)
где
Y(t)-зависимая переменная в момент времени t. f_0, f_1, f_2, ..., f_p -
оцениваемые параметры. E(t) - ошибка от влияния переменных, которые не
учитываются в данной модели. Задача заключается в том, чтобы определить f_0,
f_1, f_2, ..., f_p. Их можно оценить различными способами. Правильнее всего
искать их через систему уравнений Юла-Уолкера, для составления этой системы
потребуется расчет значений автокорреляционной функции. Можно поступить более
простым способом - посчитать их методом наименьших квадратов.
Ma(q) -модель со скользящим средним порядка q.
Модель имеет вид:
Y(t)=m+e(t)-w_1*e(t-1)-w_2*e(t-2)-...-w_p*e(t-p)
Где Y(t)-зависимая переменная в момент времени t. w_0, w_1, w_2, ..., w_p - оцениваемые параметры.
Нейросетевые модели бизнес-прогнозирования
В настоящее время, на наш взгляд, самым перспективным количественным методом прогнозирования является использование нейронных сетей. Можно назвать много преимуществ нейронных сетей над остальными алгоритмами, ниже приведены два основных.
При использовании нейронных сетей легко исследовать зависимость прогнозируемой величины от независимых переменных. Например, есть предположение, что продажи на следующей неделе каким-то образом зависят от следующих параметров:
- продаж в последнюю неделю
- продаж в предпоследнюю неделю
- времени прокрутки рекламных роликов (TRp)
- количества рабочих дней
- температуры
- ...
Кроме того, продажи носят сезонный характер, имеют тренд и как-то зависят от активности конкурентов.
Хотелось бы построить систему, которая бы все это естесственным образом учитывала и строила бы краткосрочные прогнозы.
В такой постановке задачи большая часть классических методов прогнозирования будет просто несостоятельной. Можно попробовать построить систему на основе нелинейной множественной регрессии, или вариации сезонного алгоритма aRiMa, позволяющей учитывать внешние параметры, но это будут модели скорее всего малоэффективные (за счет субъективного выбора модели) и крайне негибкие.
Используя же даже самую простую нейросетевую архитектуру (персептрон с одним скрытым слоем) и базу данных (с продажами и всеми параметрами) легко получить работающую систему прогнозирования. Причем учет, или не учет системой внешних параметров будет определяться включением, или исключением соответствующего входа в нейронную сеть.
Более искушенный эксперт может с самого начала воспользоваться каким-либо алгоритмом определения важности (например, используя Нейронную сеть с общей регрессией и генетической подстройкой) и сразу определить значимость входных переменных, чтобы потом исключить из рассмотрения мало влияющие параметры.
Еще одно серьезное преимущество нейронных сетей состоит в том, что эксперт не является заложником выбора математической модели поведения временного ряда. Построение нейросетевой модели происходит адаптивно во время обучения, без участия эксперта. При этом нейронной сети предъявляются примеры из базы данных и она сама подстраивается под эти данные.
Недостатком нейронных сетей является их недетерминированность. Имеется в виду то, что после обучения имеется "черный ящик", который каким-то образом работает, но логика принятия решений нейросетью совершенно скрыта от эксперта. В принципе, существуют алгоритмы "извлечения знаний из нейронной сети", которые формализуют обученную нейронную сеть до списка логических правил, тем самым создавая на основе сети экспертную систему. К сожалению, эти алгоритмы не встраиваются в нейросетевые пакеты, к тому же наборы правил, которые генерируются такими алгоритмами достаточно объемные. Подробнее об этом можно почитать в книге А.А. Ежова, С.А. Шумского "Нейрокомпьютинг и его применения в экономике и бизнесе".
Тем не менее, для людей, умеющих работать с нейронными сетями и знающими нюансы настройки, обучения и применения, в практических задачах непрозрачность нейронных сетей не является сколь-нибудь серьезным недостатком.
Использование многослойных персептронов
Самый простой вариант применения искусственных нейронных сетей в задачах бизнес-прогнозирования - использование обычного персептрона с одним, двумя, или (в крайнем случае) тремя скрытыми слоями. При этом на входы нейронной сети обычно подается набор параметров, на основе которого (по мнению эксперта) можно успешно прогнозировать. Выходом обычно является прогноз сети на будущий момент времени.
|
|
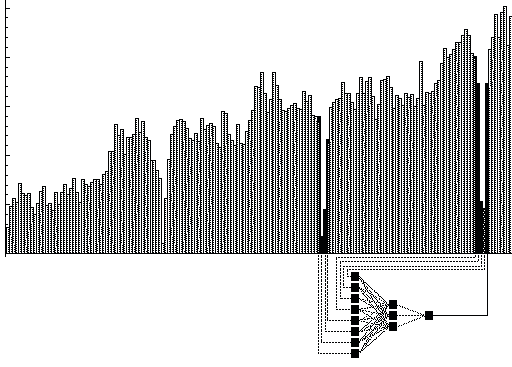
Рассмотрим пример прогнозирования продаж. На рисунке представлен график, отражающий историю продаж некого продукта по неделям. В данных явно заметна выраженная сезонность. Для простоты предположим, что никаких других нужных данных у нас нет. Тогда сеть логично строить следующим образом. Для прогнозирования на будущую неделю надо подавать данные о продажах за последние недели, а также данные о продажах в течении нескольких недель подряд год назад, чтобы сеть видела динамику продаж один сезон назад, когда эта динамика была похожа на настоящую за счет сезонности.
Если входных параметров много, крайне рекомендуется не сбрасывать их сразу в нейронную сеть, а попытаться вначале провести предобработку данных, для того чтобы понизить их размерность, или представить в правильном виде. Вообще, предобработка данных - отдельная большая тема, которой следует уделить достаточно много времени, так как это ключевой этап в работе с нейронной сетью. В большинстве практических задач по прогнозированию продаж предобработка состоит из разных частей. Вот лишь один пример.
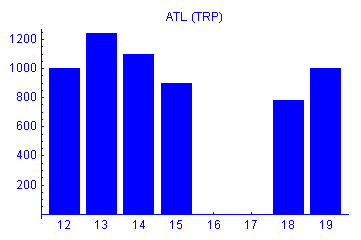
Пусть в предыдущем примере у нас есть не только историческая база данных о продажах продукта, которые мы прогнозируем, но и данные о его рекламе на телевидении. Эти данные могут выглядеть следующим образом
|
|
По оси времени отложены номера недель и рекламные индексы для каждой недели. Видно, что в шестнадцатую и семнадцатую недели рекламы не было вообще. Очевидно, что неправильно данные о рекламе подавать в сеть (если это не рекуррентная нейронная сеть) в таком виде, поскольку определяет продажи не сама реклама как таковая, а образы и впечатления в сознании покупателя, которые эта реклама создает. И такая реклама имеет продолжительное действие - даже через несколько месяцев после окончания рекламы на телевидении люди будут помнить продукт и покупать его, хотя, скорее всего, продажи будут постепенно падать. Поэтому пытаясь подавать в сеть такие данные о рекламе мы делаем неправильную постановку задачи и, как минимум, усложним сети процесс обучения.
При использовании многослойных нейронных сетей в бизнес-прогнозировании в общем и прогнозировании продаж в частности полезно также помнить о том, что нужно аккуратно делать нормировку и что для выходного нейрона лучше использовать линейную передаточную функцию. Обобщающие свойства от этого немного ухудшаются, но сеть будет намного лучше работать с данными, содержащими тренд.
Использование нейронных сетей с общей регрессией GRNN и GRNN-Ga
Еще одной часто используемой нейросетевой архитектурой, используемой в бизнес-прогнозировании является нейронная сеть с общей регрессией. Несмотря на то что принцип обучения и применения таких сетей в корне отличается от обычных персептронов, внешне сеть используется таким же образом, как и обычный персептрон. Говоря другими словами, это совместимые архитектуры в том смысле, что в работающей системе прогнозирования можно заменить работающий персептрон на сеть с общей регрессией и все будет работать. Не потребуется проводить никаких дополнительных манипуляций с данными.
Если персептрон во время обучения запоминал предъявляемые примеры постепенно подстраивая свои внутренние параметры, то сети с общей регрессией запоминают примеры в буквальном смысле. Каждому примеру - отдельный нейрон в скрытом слое сети, а затем, во время применения сеть сравнивает предъявляемый пример с примерами, которые она помнит. Смотрит, на какие из них текущий пример похож и в какой степени и на основе этого сравнения выдаст ответ.
Отсюда следует первый недостаток такой архитектуры - когда база данных о продажах, или других величинах, которые мы прогнозируем велика, сеть станет слишком большой и будет медленно работать. С этим можно бороться предварительной кластеризацией базы данных.
Второй недостаток таких сетей особенно заметен в задачах бизнес
прогнозирования - они совсем не способны "продлевать" тренд. Поэтому
такие сети можно использовать только в случаях, когда рынок устойчивый, либо,
после декомпозиции данных, тренд прогнозировать другими архитектурами нейронных
сетей, или любыми классическими методами.
Источник:http://www.neuroproject.ru/forecasting_tutorial.php
Начало
Библиотека