Рональд H. Браун, доктор философии, Брайен M. Маркс и Джордж Ф.Корлисс, доктор философии

Отдел Электрической и Компьютерной Разработки

Университет Marquette, Милуоки

 [Рональд brown|brian.marx|george.corliss] @marquette.edu

Перевод с английского языка: Алексеева Е.В

Источник: Ronald H. brown, brian M. Marx, and George F. Corliss "Mathematical Models for Gas Forecasting"

"Математические Модели Прогнозирования Потребления Газа"

1 Введение

Местная Компания Распределения (LDC) оказывается передо многими проблемами в деле поставки газа своим клиентам. Система поставки газа LDC состоит из газораспределительных станций, компрессоров, газового хранилища и клиентов. LDC должен управлять этими системами, чтобы гарантировать поставку газа в адекватных объемах необходимого давления при всех обстоятельствах. Для эффективности, экономичности и безопасности ежедневное потребление газа  клиентами должно быть известно заранее с некоторой степенью точности. В этой статье обсуждаются методы предсказания совокупного ежедневного потребления газа клиентами LDC. Подобные модели используются для предсказания почасового потребления,  а также ежемесячного и более длительного срока.

Основа клиента LDC состоит из многих индивидуальных клиентов, каждый с уникальным потребительскими особенностями. Клиенты используют газ для отопления помещений, известного как отопительная нагрузка, для нагревания воды, для сушки, приготовления и выпечки  и др. процессов, известных как базовая нагрузка, и для производства электроэнергии.

Клиентская база вообще делится на три категории:

1.  Население

2.  Коммерческие организации

3.  Индустриальные (промышленность).

Особенности потребления этих трех категорий значительно отличаются. Потребление населения - типично чувствительно к температуре, увеличиваясь по выходным. Потребление коммерческих клиентов также зависит от температуры, но уменьшается по выходным. Промышленное потребление намного меньше зависит от температуры, уменьшаясь значительно по выходным.

Исторически, много методов использовались, чтобы предсказать ежедневного потребления. Газовые диспетчеры использовали методы, типа наблюдения за потреблением в подобные дни в прошлом и распределяли объемы в соответствии с температурой. Часто эти методы успешно применены только экспертами с годами опыта в LDC.

Наряду с отменой госконтроля газовых цен появилась необходимость более точно предсказывать потребность клиента в природном газе. Многие LDC развили математические формулы, чтобы предсказать газовое потребление с различной степенью успеха. Эти модели развиваются, используя исторические данные о потреблении вместе с другими историческими данными и информацией, типа: погодных условий и дня недели.

2 Математические Модели Прогнозирования Ежедневного Потребления

Самыми обычными математическими методами моделирования, используемыми для прогнозирования ежедневного потребления, являются множественная линейная регрессия и искусственные нейронные сети. Этот раздел кратко представляет эти два метода.

2.1 Множественная Линейная Регрессия

Множественная линейная регрессия - один из самых используемых методов для моделей предсказания, и это было применено к прогнозированию. Предположим в течение дней N (1<= k <= N), у нас есть объем потребления клиента Si и М независимых факторов, xk, j, 1<= k <= N и 1<= j <= M, которые могли бы повлиять на Si. Модель оценки множественной линейной регрессии:  

где каждый ¯j - параметр, который определяет, как выход связан со входом jth. Его точность ограничена, однако, в соответствии с предположением о линейной зависимости между факторами входа и выхода (потребление газа в этом случае).

2.2 Искусственные Нейронные сети

Искусственные Нейронные сети (aNN) - математические модели, которые могут приблизить любая (нелинейная) непрерывная функция произвольно хорошо . aNN приобретает знание несмотря на учебный процесс. Построителями моделей газового потребления были привлечены aNN из-за способность отображения неизвестных нелинейных зависимостей между входами и выходом. В частности нелинейные свойства aNN учитывают прямую зависимость от температуры, скорости ветра и предшествующие температуры дня в узлах ЭНН, не учитывая взаимодействия и нелинейный отклик этих воздействий. Кроме того, учебный процесс строит взаимодействии вход-выход, которое интерполируется хорошо к ситуации, которая, возможно, точно не соответствует учебным данным. Однако, в то время как aNN весьма хороша при интерполяции решения, которое не было представлено в течение обучение, это не столь хорошо при экстраполировании вне области учебного знания. Проблема для газовой оценки, заключается в том, что если модель aNN не обучалась с историческими данными дней чрезвычайной погоды, модель не будет выполняться также в такие дни.

2.3 Динамическая Модель Адаптации

Объединение многократных прогнозов от моделей, типа искусственных нейронных сетей или множественной линейной регрессии может уменьшить ошибки, являющиеся результатом ошибочных предположений, отклонений или ошибок в данных. Многократные отдельные прогнозы могут быть объединены, используя АвтоРегрессионное Скользящее Среднее значение с внешим входом - (aRMaX) модель. Коэффициенты для множественной линейной регрессии или искусственной нейронной сети устанавливаются каждый раз, когда модель переобучается. Однако, внешние факторы позволяют aRMaX модель динамически приспособиться  каждый раз при ее использовании, например, компенсировать рост нагрузки или  изменяться в зависимости от поведения газового потребления между независимо переобученными их основных моделей. Применение Динамической Модели Адаптация к ежедневной системе прогноза потребления может уменьшить ежедневную среднюю ошибку и уменьшить худшие ошибки, вызванные необычными днями, не наблюдаемыми в учебном множестве.

3 Факторы, Влияющие На Ежедневное Потребление

3.1 Моделирование Влияния Температуры

Много факторов влияет на потребление газа. Самый существенный фактор - температура, так как большая часть газа используется для отопления помещений. Ежедневная средняя температура и ежедневное газовое потребление для региона Висконсин в сравнении с днем показываются на Рисунок 1. (Потребление клиента было представлено так, чтобы защитить секрет фирмы.)

Рисунок 1: Среднесуточная температура и ежедневное потребление газа для региона Висконсин в течение дня -точка. Один раз средняя температура достигает определенной температуры, отопление помещений больше не происходит; уровни потребления - около некоторой постоянной, известной как базовая нагрузка. Эта нелинейная особенность наблюдалась давно и использовалась для определения Затраты на отопление в день как

где Tk - средняя температура в течение kth дня, и Tref - справочная температура, исторически равна 18◦C. Газовое потребление для средней температуры в течение отдельных дней было изображено на Рисунке 2, которая иллюстрирует то газовое потребление, приблизительно пропорционально HDD (Heating Degree Day).

Рисунок 1 - Среднесуточная температура и ежесуточное потребление природного газа в Висконсин в зависимости от дня

Модель с 2 параметрами: потребление в течение kth дня может быть оценено как базовая нагрузка плюс отопительная нагрузка, умноженная на HDDk:

Модель с 3 параметрами: Со временем, справочная температура  HDD изменилась. Один из путей приспособиться к этому изменению - добавить второй фактор HDD к модели. Здесь мы добавляем второй фактор HDD с температурой рекомендации 55◦F, который автоматически генерирует оптимальную температуру рекомендации HDD,  как показано на Рисунок 3.

Модель с 5 параметрами: Потери тепла(высокая температура) - динамический процесс. Добавление условия HDD из предыдущего дня может улучшить точность модели. Добавление условия охлаждения CDDk =Макс (Tk − Tref, 0) может также улучшить точность модели. Оба условия были добавлены к модели bSk = ¯0 + ¯1HDD65

где

 

          Рисунок 2 - Поле рассеивания потребления газ в зависимости от температуры

 

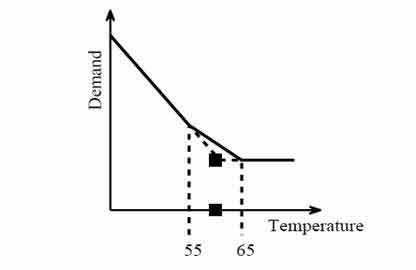
Рисунок 3 - Добавление второго условия HDD имеет эффект автоматической оптимизации рекомендуемой температуры HDD.

 

3.2 Моделирование Влияния Ветра

Другой важный фактор - ветер, потому что здания теряют больше тепла в ветреный день, чем в  спокойный день. Ветер мог быть добавлен как другое условие к моделям выше, но тогда влияние ветра было бы тем же самым при всех температурах, в то время как известно, что воздействие ветра увеличивается с HDD.

Метод, который работает хорошо, должен использовать HDD, приспособленный к влиянию Ветра (HDDW). Они вычисляются различными способами. Если WS - скорость ветра в миль/ч, мы можем вычислить

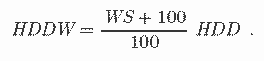
3.3 Потребление За Предыдущий День

Как правило, прогнозы нагрузки делаются для наступающего дня прежде, чем газовый день текущего дня полон. Таким образом, потребление текущего дня неизвестно. Однако, вчера является законченным, таким образом поток в течение того дня известен. Добавляя это и более ранние ежедневные потоки как входы к модели прогноза могут значительно уменьшить ошибки прогноза.

3.4 Моделирование Дня Недели

Газовое потребление отличается в различные дни недели. Например, по выходным, потребление населения увеличивается, потребление обычно больше, чем возмещение от уменьшения потребления от обоих коммерческого и промышленного потребление. При прогнозировании нагрузки используется много методов, которые пытаются учитывать этот эффект, прежде всего, добавляя индикатор "день недели" ко входным параметрам.

Индикатор Weekday/Weekend: двоичная переменная индикатора может быть добавлена к модели к различным дням выходных. Таким образом, переменная Выходной - 1 по субботам и воскресеньям и 0 в другие дни недели. Это условие может быть добавлено к любой из моделей, описанных выше.

В пятницу индикатор: Так как газовый день в пятницу включает запуск в субботу утром, типично потребление в пятницу ниже, чем в другие будние дни, все же выше чем требования субботы и воскресенья. Это влияние изменяется от региона к региону в LDC и, конечно, по всей стране. Это влияние может быть объяснено установкой переменной индикатора в число между 0 и 1 по пятницам.

Индикаторы Синус/Косинус: Периодические явления могут быть представлены рядом Фурье. Дни недели являются периодическими с периодом в семь дней, таким образом, мы можем использовать "день недели" переменную DOW для представления основной частоты семи дней:

1 = воскресенье,

2 = понедельник, и т.д.:

Задержка семи дней: Другая техника улучшения прогноза потребления включает оба требования: и температура за семь дней назад, если день семью днями ранее не был праздничным(выходным).

3.5 Праздничные и Предпраздничные Дни

Праздничные и предпраздничные дни обычно имеют более низкие объемы потребления, чем если бы день не был праздником. Один подход, который может использоваться с или без вышеупомянутого подхода регулирования дня недели -  усреднить остаточные ошибки в обучающем наборе данных на определенный праздник и приспособить прогнозируемое потребление. Например, если, после записи в параметрической форме нашей модели, мы оцениваем модель на все дни нового года  в обучающем наборе и вычисляют ошибку прогноза как прогноз потребления минус фактический поток, и вычисляют средние ошибки, мы можем вычесть эту среднюю ошибку для приспособления прогноза к дню нового года. Праздничная корректировка состоит в том, чтобы притвориться, что день - суббота. Это фактически работает весьма хорошо. Предпраздничные дни могут также быть приспособлены, то есть  день перед праздником может считаться пятницей, или когда праздник попадает на понедельник, считают воскресенье  субботой  и  праздник (понедельник) - воскресеньем.Модели, которые используют требования с предыдущих дней, слабо влияют в дни после праздника,  низкое потребление в праздники  - теперь вход модели. Это низкое потребление в праздника может быть приспособлено добавлением к средней ошибке, чтобы считать день как непраздник.

3.6 Прогнозирование Сельскохозяйственного Потребления

Различные сельскохозяйственные процессы используют природный газ, таких как: консервирование помидоров и сушка зерна. Естественный газ, потребляемый в сельскохозяйственных целях обычно используется в процессах, связанных со сбором урожая.Сельскохозяйственное использование природного газа в большой степени, но не исключительно зависит от погоды, но иначе, чем потребление населения. Эти сельскохозяйственные процессы обычно происходят осенью, в течение или вскоре после сбора урожая. Следовательно, пиковое сельскохозяйственное потребление приходится на осень, тогда как пик потребления населением приходится на зиму. Прежде всего принципиальное знание роста, урожая, подготовки или обработки урожая в географической области могут быть применены, наряду с регрессионным анализом и теорией оптимизации прогнозирования ежедневного сельскохозяйственное потребление природного газа от урожая.

3.7 Другие Факторы

Много других потенциальных факторов существуют, типа солнечного излучения, направление ветра, температура воды из крана, ценовая политика, нормы потребления  и промышленные нормы производства, чтобы не назвать многих. Некоторые из них факторы могут быть непосредственно измерены, в то время как другие не могут, или по крайней мере, не могут быть достаточно измерены.

4 Качествo Данных

При построении моделей по историческим данным, тремя самыми важными характеристиками  при обучении набора данных являются качество данных, качество данных и качество данных. Большинство образцовых алгоритмов приспособления, включая линейную регрессию и aNN обучающие методы, обсужденные выше, предназначены для минимизации ошибки среднеквадратичного отклонения - форма квадратичной ошибки. Если учебные данные содержат ошибки, модель не будет давать хорошего соответствия.

Очистка данных: лучший план действий должен начаться с хороших данных, но достаточно многие хорошие исторические данные не всегда доступны. Часто возможно использовать предварительные модели прогнозирования потребления, чтобы обнаружить аномальные данные, которые могут быть подтверждены, исправлены или отброшены прежде, чем заключительные модели построены.

Разсосредоточение данных: Точно так же для некоторого LDC, единственные исторические доступные данные потребления могут быть (приблизительными) ежемесячно, хотя необходимы ежедневные  прогнозы. Часто возможно использовать предварительные модели прогноза, чтобы разъединить ежемесячные данные на приблизительные исторические ежедневные данные перед заключительным построением модели. Подобные методы могут использоваться, чтобы дать хорошие прогнозы по часам при ненадежных почасовых потоков данных.

Число дней обучения:обучая aNN эвристически, в десять раз больше учебного набора векторные пары как веса необходимы. Иначе, aNN " запомнит" обучающие векторные пары и не будут хорошо определять тенденции в данных. Эти явления запоминания известны как перетренировка или сверхприспособление. Подобные проблемы происходят с линейными моделями регрессии, если обучение набора данных не является достаточно большим или достаточно богатым. Мы используем базу данных приблизительно 250 000 газовых дней почти от 100 регионов по всей стране для образцового развития модели, таким образом мы в состоянии выявлять новшества модели экстенсивно.

Рост базы клиентов: Модели развиваются от очень большой основы опыта, но модели для LDC обучаются на исторических данных от этого LDC. Наивное использование только несколько лет истории потребления газа часто уместна. Более давние данные - не хороший признак роста количества потребителей и управления стороны потребления.Из-за этой не стационарности потребителей, построение модели прогнозирования потребления на следующий отопительный сезон затруднительно, но с ростом корректировок  может быть рассчитана. Для иллюстрации этого рассмотрим пример. Предположим, что модель построена, используя данные за последние пять лет из функционирующей области с существенным ростом. Если все дни в обучающем наборе данных имеют одинаковый вес, модель лучше всего предсказывает нагрузку для среднего потребителя в обучающем наборе данных. Остаточные ошибки модели будут наименьшими для середины года. Ошибки будут положительными (прогнозируемое значение больше, чем фактическое потребление) за первые два года обучающих данных, и будет отрицательным (прогнозируемые значение меньше, чем фактическое потребление) за прошлые два года обучающих данных. Наша цель состоит в том, чтобы строить модель прогнозирования потребления на наступающий отопительный сезон. Эта модель лучше всего предскажет отопительный сезон трех предшествующих лет.

Эта проблема может быть частично преодолена "выращиванием" более старых исторических данных. Простой путь к выращиванию исторических данных (статистики) сделать их подобными тем, которые встречались в течение самого последнего отопительного сезона. Это достигается  первым вычислением линейной регрессионной модели для каждого отопительного сезона. Потребление отопительных сезонов до предыдущего может быть приспособлено (отрегулировано)  добавлением фактора базовой нагрузки к каждому дню, чтобы сделать базовые нагрузки теми же самыми как в предыдущий сезон и добавлением дополнительного условия, пропорционального HDD каждого дня, чтобы сделать использование в  HDD тем же самым как использование в HDD в течение предыдущего сезона.

Например, используя только данные 2004-2005 годов, мы строили модель с 2 параметрами

и используя только данные 2003-2004 годов, мы строили модель с 2 параметрами

Мы тогда выращивали 2003-2004 данные  отопительного сезона как

Теперь "новые" 2003-2004 данных то потреблении  имеют ту же самую базовую нагрузку и фактор (коэффициент) отопительной нагрузки как данные 2004-2005 годов.Ожидаемое потребления: модели, использующие ожидаемые, предскажут ожидаемое. модели, построенные с использованием данных о потреблении, предскажут потребление. В большинство дней, ожидаемая равняется потреблению. В дни, когда отключают клиентов, включают и т.д., газ, который течет через городские распределительные станции, меньше, чем потребность.

На рис.4 показаны фактические ожидаемые в зависимости от температуры для области с потребителями, поставка газа которым может быть прекращена. "Наклонный" эффект при более холодных температурах обусловлен отключаемыми клиентами. Чтобы сделать ожидаемую, прогнозирующей модели, предсказанием потребления, исторические(статистические) обучающие данные  должны быть дополнены предполагаемыми отключениями  и т.д., так, чтобы построенная модель, используя эти данные, предсказала потребление.

Действующие области: Точность прогноза часто может быть улучшен, подразделяя область (регион), для которой необходимо спрогнозировать потребление, в меньшие области и делается прогноз для каждой области с отдельно обучаемыми моделями. Меньшие области могут извлечь больше пользы из более точных средних прогнозов погоды, из более гомогенетической основы потребителя  или от других факторов.

Многочисленные метеостанции: Точность прогноза может часто улучшаться при использовании тщательно настроенного взвешенного среднего числа прогнозов погоды от многочисленных метеостанций в или около цели в области.

Обобщение, интерполяция и экстраполяция: Были сделаны утверждения, что aNN превосходные  обобщители; что aNN может изучить общие тенденции из обучающего  набора данных и после может дать действительные оценки для входа, который не учитывался прежде. Это - половина правды. Это верно, если вход подобен входам в обучающих данных, но ложно, если вход не подобен какому-либо из входов в обучающих данных. Лучший способ точно определить способности aNN - то, что это интерполирует хорошо, но вообще, это экстраполирует неочевидно. Напротив, линейная модель регрессии экстраполирует очень очевидно, и в случае прогнозирования газового потребления  весьма хорошо.

 

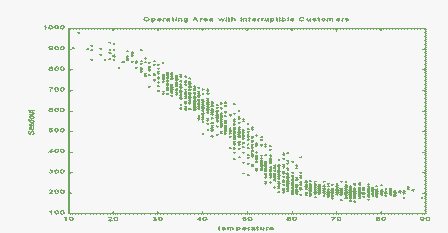
Рисунок 4 - Ожидаемые значения в зависимости от температуры для области с потребителями, поставка газа которым может быть прекращена

Это подразумевает, что оценки потребления aNN модели преуспеют в дни, которые являются подобными историческим дням в обучающем наборе, и не так хороши в дни, которые не подобны дням в обучающем наборе. Это  вызывает проблемы оценок потребления в пиковые дни и даже необыкновенные дни (дни, которые являются значительно более холодными, более теплыми или более ветреными, чем нормальные, дни, которые намного более теплые или более холодные, чем предыдущий день и т.д.).

На рис.5 показана зависимость температуры от ветра для обучающего набора (12-Ноября-1994 - 31-Мая-1997) и набор испытания (1-Июля-1997 - 1-Июня -1998) для aNN обучался для 1997-1998 отопительного сезона. Даже при том, что 1997-1998 отопительный сезон был умеренный (мягкий), набор испытания (отопительный сезон) содержащий много ветреных дней, которые не были подобны каким-либо дням в обучающем наборе, который включает только два ветреных дня. Существует два подхода решить эту проблему (1) -  использование больше (и старше) обучающих данных и (2) - подготавливают дополнительные обучающие данные.

Надбавка данных: В Милуоки, Wi, сегодняшняя средняя температура - в пределах 8◦F от вчерашней температуры приблизительно 80 %. Однако, вопрос прогнозирования потребления природного газа  нетипичный день, но необычный день. Если мы строим модели, используя равную надбавку всех данных, дней, где сегодняшняя температура - больше чем 8◦F, вчерашняя температура будет взвешена как 1/4  столь же важный как другие дни. Однако, это дни, в которые существует потребность LDC в хорошие прогнозы, и прогнозирование является самым трудным. Усилия предпринятые для идентификации необычных дней, таких как сегодня намного более холоднее  или более теплее, чем вчера, намного более холоднее или более теплее, чем нормальный, намного более ветреный, чем нормальный  и т.д., так в эти дни могут быть учтены более в большой степени в учебном процессе модели.

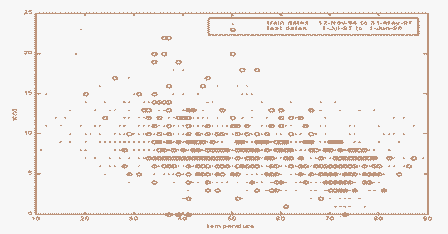
Рисунок 5 - Зависимость температуры и ветра для обучающего и испытательного наборов данных

 Резюме.

В этой статье мы описали две важных модели, соответствующие алгоритмам, используемым для прогнозирования ежедневного естественного газопотребления: множественная линейная регрессия и искусственные нейронные сети. Воздействия температуры, ветер, погода  предшествующего дня, потребление предыдущего дня, день недели  и праздники на газопотребление были обговорены, наряду с общими проблемами качества данных таких как:  длины обучающего набора, различия между ожидаемой и потреблением, ростом числа потребителей. Наш опыт состоит в том, что необходимо применение модели с использованием комбинации множественной линейной регрессии и искусственных нейронных сетей - очень точные инструменты для того, чтобы предсказать ежедневное газопотребление.

Источник: Ronald H. brown, brian M. Marx, and George F. Corliss "Mathematical Models for Gas Forecasting"