RUS | UKR | ENG || ДонНТУ || Портал магістрів ДонНТУ
Автобіографія
Магістр ДонНТУ Блінов Юрий Валерійович

Блінов Юрій Валерійович

Факультет комп´ютерних наук и технологій

Спеціальність: Комп'ютерні системи та мережі

«Розробка і дослідження методів та структур апаратної генерації тестів і аналізу тестових реакцій на базі FPGA»


Разработка і дослідження методів та структур апаратної генерації тестів і аналізу тестових реакцій на базі FPGA


Змiст

  1. Вступ і актуальність
  2. Мета і завдання магістерської роботи
  3. Наукова новизна
  4. Принципи цифрового тестування
  5. Методи генерації тестових впливів
  6. Аналіз тестових реакцій
  7. Розроблена структура логічного аналізатора
  8. Результати роботи
  9. Висновки
  10. Список літератури

Вступ і актуальність

Проблема тестування та діагностики стала актуальною з початком виробництва перших дискретних пристроїв. Незважаючи на те, що на даний час процес виробництва схем практично повністю автоматизований, це не гарантує якість кожного виробленого чіпа. Причинами дефектів, окрім інших, можуть послужити домішки і дефекти матеріалів, неправильна робота обладнання або людський фактор.

Існують безліч класів пристроїв, вимоги до справності яких, є особливо критичними. Одним із способів забезпечення надійності, як в процесі виробництва, так і в процесі експлуатації є застосування засобів і методів технічної діагностики, що дозволяють здійснювати контроль, локалізацію несправності, і відновлення апаратури шляхом заміни некоректно працюючого блоку, або пристрою.

Суттєвим параметром при тестуванні пристроїв є швидкість тестування. Існують автоматизовані системи тестування (ATE), що дозволяють працювати на частотах рівних десяткам гігагерц[2]. Дані пристрої дорогі, масивні і стаціонарні, що обмежує їх застосування.В свою чергу, технологія FPGA, що стала популярною, дозволяє створювати швидкі компактні і не дорогі пристрої. Тому тема даної магістерської роботи, спрямована на розробку і дослідження методів і структур апаратної генерації та аналізу дискретних тестових реакцій, з використанням всіх переваг технології FPGA є актуальною.


Мета і завдання магістерської роботи

Метою роботи є розробка структур і методів для автоматизації процесу генерації тестових впливів і аналізу тестових реакцій. Для досягнення поставленої мети в роботі ставляться наступні завдання:

  • дослідження існуючих методів і систем діагностування;
  • розробка методів і FPGA‐структур генерації дискретних тестових реакцій;
  • розробка методів і FPGA‐структур аналізу дискретних тестових реакцій;
  • розробка та дослідження експериментальної підсистем генерації тестових впливів і аналізу тестових реакцій на базі FPGA.

Наукова новизна

Передбачувана наукова новизна полягає в розробці методу та архітектури генератора тестових впливів і аналізатора тестових реакцій на базі FPGA з метою забезпечення можливості тестування швидкодіючих цифрових пристроїв. Очікується, що розроблена підсистема буде забезпечувати досить високу швидкодію, компактність, універсальність, а також помірно низьку вартість.


Принципи цифрового тестування

На рисунку 1 продемонстрований основний принцип тестування.


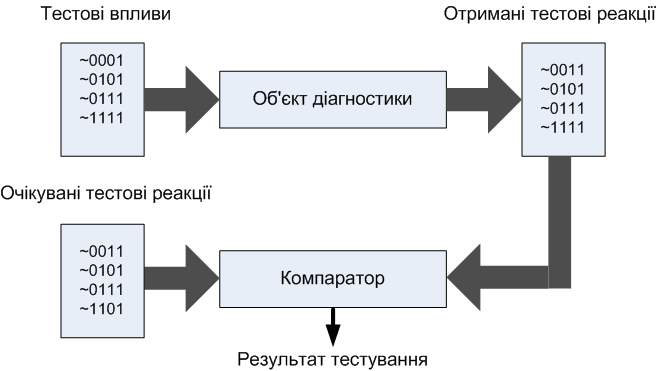
Прінцип тестірованія

Рисунок 1 — Принцип тестування [2]

З рисунку видно, що тестові впливу (тестові вектори) посилаються на входи схеми, з виходів схеми знімаються тестові реакції, і перевіряються на ідентичність з очікуваними тестовими реакціями. Також порівнюватися можуть не самі вектори тестових реакцій, а їх сигнатури, що дозволяє істотно знизити витрати пам'яті. Якщо відмінності між отриманими та очікуваними значеннями немає, то пристрій проходить тестування. Тестування проводиться автоматизованою системою, яка сама по собі є дуже складним пристроєм.


Методи генерації тестових впливів

Процес генерації тестових впливів полягає в послідовній видачі на входи об´єкту діагностики тестових векторів ti, i = 1 .. n, з деякої безлічі T = (ti), званої тестом. Порядок проходження тестових впливів може бути не важливим або строго обумовленим. Залежно від зазначених ознак розрізняють наступні методи генерації тестових впливів[1]:

  • вичерпні;
  • псевдовипадкові;
  • детерміновані;
  • комбіновані.

Вичерпне тестування

При вичерпному тестуванні тест Т утворює 2n вхідних значень, де n — кількість входів, які подаються на об´єкт діагностики, причому порядок тестових векторів не важливий. Даний спосіб досить простий в реалізації, тому що може бути реалізований з використанням двійкового лічильника потрібної розрядності. Однак, цей метод не може бути використано для послiдовнiсних схем, що пояснюється поганими кореляційними властивостями векторів вичерпного тесту.

Послiдовнiсі схем — це схеми, вихідні сигнали яких у загальному випадку, залежать не тільки від комбінацій вхідних, але й від значення самих вихідних сигналів у попередній момент часу, наприклад всілякі елементи пам´яті.

Кореляція — термін, що визначає підтвердження зв´язку між двома явищами, подіями або процесами, характер функціональної залежності між якими точно не встановлено[3].


Псевдовипадкове тестування

При псевдовипадковому тестуванні також генерується тест, близький до вичерпного, проте, на відміну від останнього порядок векторів псевдовипадкового тесту володіє властивостями, близькими до характеристик випадкової послідовності.

Одним із варіантів реалізацій, що використовуються для генерації псевдовипадкових послідовностей, є реалізація з використанням регістра зсуву з лінійними зворотними зв'язками (РЗЛЗЗ)[9].

Для генерації псевдовипадкових послідовностей застосовують дві схожі структури. На рисунку 2 показано РЗЛЗЗ із зовнішніми суматора зворотного зв´язку, а рисунок 3 мыстить РЗЛЗЗ з внутрішніми суматора зворотного зв´язку[3].

РЗЛЗЗ із зовнішніми суматором зворотного связі

Рисунок 2 — РЗЛЗЗ із зовнішніми суматором зворотнього зв´язку [3]


РЗЛЗЗ з внутрішніми суматором зворотного связі

Рисунок 3 — РЗЛЗЗ з внутрішніми суматором зворотнього зв´язку [3]

Важливою характеристикою РЗЛЗЗ є період повторення послідовності, що генерується, який залежить від виду зворотного зв´язку. Зворотній зв´язок описується поліномом зворотного зв´язку G(x). Доведено, якщо G(X) примітивний, а значить поліном, що не приводиться, то на виходах РЗЛЗЗ генерується періодична послідовність з максимальним для розрядності n періодом слідування сигналів, рівним L = 2n −  1. Такі послідовності називаються послідовностями максимальної довжини або М‐послідовностями[3].


Генетичні алгоритми

Досить новим методом генерації псевдовипадкових тестів є метод із застосуванням генетичних алгоритмів[4]. Використання генетичних алгоритмів при генерації перевіряючих тестів є природним розвитком псевдовипадкових методів генерації тестів. Одним з перших застосувань генетичних алгоритмів в технічній діагностиці цифрових схем є побудова на їх основі генераторів тестових послідовностей. Суть завдання полягає в пошуку двійковій вхідної послідовності, яка для кожної несправності з заданої множини дає різні вихідні значення сигналів у справній і несправній схемах. Генетичні алгоритми, будучи однією з парадигм еволюційних обчислень, представляють собою алгоритми пошуку, побудовані на принципах, подібних до принципів природного відбору. Ці принципи грунтуються на наступних механізмах еволюції:

  • перший принцип генетичних алгоритмів заснований на концепції виживання найсильніших і природного відбору за Дарвіном. Згідно Дарвіну особини, які краще здатні вирішувати завдання в своєму середовищі, виживають і більше розмножуються (репродукують). У генетичних алгоритмах кожна особина є певним рішення даної проблеми;
  • другий принцип генетичних алгоритмів обумовлений тим фактом, що хромосома нащадку складається з частин, що отримані з хромосом батьків;
  • третій принцип, який використовується генетичними алгоритмами, заснований на концепції мутації. Спочатку цей термін використовувався для опису істотних змін властивостей нащадків і набуття ними властивостей, відсутніх у їхніх батьків. За аналогією з цим принципом генетичні алгоритми використовують подібний механізм для зміни властивостей нащадків і тим самим, підвищуючи різноманіття (мінливість) особин в популяції (безлічі рішень). Ці три принципи складають ядро генетичних алгоритмів. Відповідно до них простий генетичний алгоритм використовує три основних оператора: репродукція, кросинговер, мутація

Особиною (хромосомою) в даному випадку є окремий двійковий набір значень вхідних змінних схеми[7]. Популяцією є безліч наборів, складових перевіряючий тест схеми. Як цільова (fitness) функції можна використовувати число несправностей, що їм можна перевірити. Слід підкреслити, що значення цільової функції визначається за допомогою програми логічного моделювання[5], яка є важливим компонентом цього методу.

Псевдовипадкове тестування дозволяє з високою імовірністю покривати несправності комбінаційних і нескладних послiдовнiсних схем. Ефективність даного виду тестування падає зі збільшенням складності об'єкта діагностики, а для складних (сильно последовательностних) схем він є практично неприйнятним з виявляв здібності, так як такі схеми вимагають суворо регламентованого порядку проходження тестових впливів. Для таких схем використовують детерміноване тестування[1].


Детерміноване тестування

При детермінованому тестуванні визначаються значення усіх векторів тесту або його деякої підмножини. Якщо порядок проходження векторів тесту також має значення, то тест називається сильно‐детермінованим, якщо порядок може бути довільним, то тест називається слабо-детермінованим.


Слабо‐детерміновані тести

Для слабо‐детермінованого тесту Т знімаються обмеження на порядок його векторів. Очевидно, що два тести з різною послідовністю тестових векторів мають однакову виявляючу здібність. Ці два чинники використовуються для полегшення процесу створення тесту і зниження, тим самим, апаратурних витрат на реалізацію його генератора. Разом з тим це сприяє тому, що генератор такого тесту може бути використаний тільки для комбінаційних схем, тому що для них не важливий порядок проходження вхідних векторів.

До генераторам слабо‐детермінованих тестів відносять[1]:

  • генератори на базі композиції ПЗП та лінійної последовностної машини («ПЗП + ЛПМ»),
  • ПЗП, лічильника та формувача («ПЗП + СТ + С»),
  • генератор на базі регістра зсуву з нелінійним зворотним зв'язком (РЗНЗЗ)[10].


Сильно‐детерміновані тести

На відміну від раніше розглянутого, для генерації сильно‐детермінованого тесту може бути використана тільки одна конструкція, яка виконується на основі пристрою пам´яті ємністю n × m. Для детермінованого тесту визначаються значення усіх векторів і порядок їх надходження. Це досить жорсткі вимоги, сильно ускладнюють побудову компактного генератора. Даний вид генераторів дозволяє з високою ефективністю виконувати тестування цифрових схем будь‐якої складності. Однак, навіть для нескладних ОД такий генератор відрізняється великими апаратурними витратами.

Таким чином, розглянуті методи і засоби генерації вичерпних, псевдовипадкових і слабо‐детермінованих тестів характеризуються великою компактністю, але є не ефективними для сильно послiдовносних схем. Строго‐детерміновані тести, навпаки, забезпечують тестованність схем будь‐якої складності, але не існує методів їх компактної генерації.


Комбіновані тести

Очевидним підходом подолання зазначених недоліків є використання комбінованих способів тестування, які базуються на поєднанні суворо детермінованих та інших типів тестових послідовностей. Серед комбінованих методів поширений підхід поєднання детермінованих та псевдовипадкових послідовностей, який полягає в тому, що на інформаційних входах ОД генерується псевдовипадкові тести (також тести згенеровані за допомогою генетичних алгоритмів), а на керуючі входи подаються сильно‐детерміновані послідовності. Однак, такий підхід лише незначно скорочує ємність детермінованої складової.


Аналіз тестових реакцій

Аналіз тестових реакцій здійснюється шляхом порівняння одержуваної реакції з еталонною, яка може бути отримана або з фізичного еталонного пристрою, або за допомогою його логічної моделі. При цьому порівнюватися можуть повні реакції або їх стислі еквіваленти (сигнатури). Відповідно до цього розрізняють наступні основні способи аналізу тестових реакцій:

  • логічний аналіз;
  • компактний аналіз;
Серед методів останнього типу найбільшого поширення набули[1]:
  • сигнатурний аналіз — заснований на стисканні ТР за допомогою регістра зсуву, охопленого ланцюгами лінійних зворотних зв´язків;
  • рахунок станів — двійковий лічильник що підраховує кількість одиниць і нулів;
  • рахунок переходів — двійковий лічильник що підраховує кількість переходів з 0 в 1 або з 1 в 0;

Розроблена структура логічного аналізатора

На момент написання реферату на базі налагоджувальному комплексу Spartan‐3E розроблений логічний аналізатор. Спрощена структура розробленого логічного аналізатор наведена на рисунку 4.


Структура логічного аналізатору

Рисунок 4 — Структура розробленого логічного аналізатора
(GIF‐анiмацiя, розмiр: 113 КБ, кiлькicть кадрiв:11, кiлькicть повторень:5)

Логічний аналізатор — пристрій, призначений для запису та аналізу цифрових послідовностей. Вони зазвичай використовується для збору даних у системах, що мають занадто багато каналів, щоб бути дослідженими за допомогою звичайного осцилографа[6].

Розроблений пристрій має наступний принцип роботи:

  • користувач, використовуючи клієнтську програму вибирає і встановлює необхідні параметри, які використовуються для вибору моменту початку реєстрації сигналів з досліджуваного пристрою.
  • коли всі необхідні параметри встановлені, пристрій очікує появи заданого виду сигналу на зовнішніх виходах досліджуваного об´єкта.
  • при реєстрації сигналу, що задовольняє заданим критеріям відбувається збереження сигналів із зовнішніх виходів схеми досліджуваного пристрою в пам´ять.
  • по закінченню збереження заданої кількості зареєстрованих станів дані передаються в клієнтську програму користувача, де і відбувається відображення часової діаграми.
  • пристрій переходить в режим очікування подальших команд.

Результати роботи

На момент написання реферату були отримані наступні результати:

  • виконано огляд існуючих методів тестування цифрових схем;
  • виходячи з технічних характеристик обрана FPGA‐плата на якій планується реалізація проекту;
  • виконано розробка пристрою логічного аналізатора;

Висновки

На основі вищевикладеного матеріалу можна зробити висновок, що:

  • розробка та дослідження методів і структур апаратної генерації тестів і аналізу тестових реакцій залишається актуальною;
  • на основі даних характеристик та описів методів генерації тестових векторів і аналізу тестових реакцій зроблені висновки про доцільність вибору методів при тестуванні різних класів пристроїв;
  • в якості платформи для реалізації був обраний налагоджувальний FPGA комплекс Spartan‐3E.


Список літератури

  1. Зинченко Ю.Е. Методы и средства встроенного тестового диагностирования специализированных устройств сетей передачи данных реального времени / Ю.Е Зинченко // Диссертация на соискание уч. степени канд. техн. наук.; специальности: 05.13.13 «Вычислительные машины, комплексы, системы и сети» и 05.13.05 «Элементы и устройства вычислительной техники», Институт проблем моделирования в энергетике (ИПМЭ) АН Украины. — Киев, 1989, 208c.
  2. Agrawal V.D. Essentials of electronic testing for digital, memory and mixed-signal VLSI circuits./V.D.Agrawal// Kluwer Academic Publishers, 2000, — 690c.
  3. Зинченко Ю.Е. Разработка компьютерных систем на базе ACTIVE-HDL, методические указания [Електронний ресурс] Режим доступу: http://hardclub.donntu.ru/methods/nkd/nkd_mu/MAIN.HTM
  4. Скобцов Ю.А. Логическое моделирование и тестирование цифровых устройств/ Ю.А.Скобцов, В.Ю. Скобцов // Донецк: ИПММ НАН Украины, ДонНТУ,2005. — 436с.
  5. Ivask E., Raik J., Ubar R. Comparison of Genetic and Random Techniques for Test Pattern Generation [Електронний ресурс] Режим доступу: http://www.citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.59.8973
  6. Перцовский М., Воробьев Е., Трифонов А. Применение логических анализаторов в тестировании цифровой техники [Електронний ресурс] Режим доступу: http://www.cta.ru/cms/f/?/366656.pdf
  7. Уколов И.В. Cинтез псевдослучайных контролирующих тестов для дискретного устройства [Електронний ресурс] Режим доступу: http://www.sgu.ru/files/nodes/37509/Ukolov(64-70).pdf
  8. Zhang Y., Agrawal V.D. An Algorithm for Diagnostic Fault Simulation [Електронний ресурс] Режим доступу: http://www.eng.auburn.edu/~agrawvd/TALKS/LATW10/latw10_yu_new6.pdf
  9. Linear feedback shift register. Википедия свободная энциклопедия [Електронний ресурс] Режим доступу: http://en.wikipedia.org/wiki/Linear_feedback_shift_register
  10. Non-Linear Feedback Shift Register. Википедия свободная энциклопедия [Електронний ресурс] Режим доступу: http://en.wikipedia.org/wiki/NLFSR

Примітка

При написанні даного автореферату магістерська ще не завершена. Дата остаточного завершення роботи: грудень 2010 р. Повний текст роботи та матеріали по темі роботи можуть бути отримані у автора або його наукового керівника після зазначеної дати.