При встановленні діагнозу і проведенні лікування лікарі все частіше покладаються на медичні зображення, до яких відносяться рентгенограми, УЗД, магнітно-резонансна томографія (MRI - Magnetic Resonance Imaging), комп'ютерна томографія (CT - Computed Tomography), томографія на позитивному випромінюванні (PET - Positive Emission Tomography) і т.п. Використання медичних зображень зростає з кожним роком, у наслыдок впровадження новітньої медичної техніки в лікарнях і діагностичних центрах. Об'єкти на медичних зображеннях володіють великою складністю і багатофакторністю, що обумовлює високі вимоги до надійності, точності та достовірності результатів досліджень. Швидкий розвиток цифрової і аналогової техніки останнім часом відкриває нові можливості перед розробниками. Наприклад, збільшення швидкодії обчислювальної техніки дозволяє використовувати складні, критичні до часу алгоритми, а завдяки появі кольорових телевізійних датчиків високого дозволу можна отримувати і обробляти кольорові зображення. Саме нові технічні можливості дозволяють значно розширити коло досліджень, відкривають нові шляхи вирішення завдань, що стосуються аналізу зображень.

Сьогодні весь світ прагне до автоматизації процесів у всіх сферах життя людини. Медицина - не виняток. З кожним роком все більше медичної техніки з"являється в лікарнях і поліклініках. Саме нові технічні можливості дозволяють значно розширити коло досліджень, відкривають нові шляхи вирішення завдань. У наслідку цього з'являється більше інформації, значна частина яких міститься в зображеннях.

Медичні зображення дають основний обсяг інформації про пацієнта, для вилучення якої, потрібен їх аналіз. Однією з головних частин автоматизації вимірювання оптичних і геометричних параметрів є виділення об'єктів на препаратах. Ця задача вирішується за допомогою методів і засобів цифрового аналізу зображень. Сегментація медичного зображення є складним завданням, методи для вирішення якої вибираються у відповідності із характеристиками і властивостями, що аналізують зображення.[2] Кластеризація методом К-середніх - добре відомий метод визначення приналежності елементів кластерам за допомогою мінімізації різниці між елементами кластеру та максимізації відстані між кластерами. Слово «середні» у назві методу відноситься до центроїдів кластерів. Центроїд - точка даних, яка вибирається довільно, а потім ітеративно уточнюється, поки не починає представляти собою справжнє середнє всіх точок даних кластеру. «К» означає довільну кількість точок, що використовуються для формування початкових значень процесу кластеризації. Алгоритм К-середніх обчислює квадрати евклідових відстаней між записами даних у кластері і вектор, що представляє собою середнє даного кластеру. Метод сходиться, видаючи остаточний набір з К кластерів, коли згадана сума мінімізована. Алгоритм К-середніх призначає кожній точці даних рівно один кластер і не допускає невизначеності у приналежності точки кластеру. Приналежність до класу виражається відстанню від центроїд. Зазвичай алгоритм К-середніх використовується для створення кластерів безперервних атрибутів, для яких нескладно обчислити відстань до середнього. Однак реалізація Майкрософт використовує метод К-середніх і для кластеризації дискретних атрибутів за допомогою ймовірностей. [3]

Ідея мурашиного алгоритму - моделювання поведінки мурах, пов'язаного з їх здатністю швидко знаходити найкоротший шлях від мурашника до джерела їжі та адаптуватися до змінних умов, знаходячи новий найкоротший шлях. При своєму русі мураха залишає на своєму шляху феромон, і ця інформація використовується іншими мурашками для вибору шляху. Це елементарне правило поведінки і визначає здатність мурашок знаходити новий шлях, якщо старий виявляється недоступним.
Розглянемо випадок, показаний на малюнку 1.

Коли на оптимальному шлясі (Рисунок 1 А) виникає перешкода (Рисунок 1.В) мурашкам необхідно визначити новий оптимальний шлях. Дійшовши до перепони, мурахи з однаковою ймовірністю будуть обходити її справа і зліва. Те ж саме буде відбуватися і на зворотньому боці перешкоди. Однак, ті мурахи, які випадково виберуть найкоротший шлях, будуть швидше його проходити, і за кілька пересувань він буде більш збагачений феромоном. Оскільки рух мурашок визначається концентрацією феромону, то наступні будуть віддавати перевагу саме цьому шляху (Малюнок 1.D), продовжуючи збагачувати його феромоном до тих пір, поки цей шлях з якої-небудь причини не стане недоступний.
Позитивний зворотній зв'язок швидко призведе до того, що шлях найкоротший стане єдиним маршрутом руху більшості мурашок. Моделювання випаровування феромону - негативного зворотного зв"язку - гарантує нам, що знайдене локально оптимальне рішення не буде єдиним - мурашки будуть шукати й інші шляхи. Якщо ми моделюємо процес такої поведінки на деякому графі, ребра якого являють собою можливі шляхи переміщення мурашок, протягом певного часу, то найбільш збагачений феромоном шлях по ребрах цього графа і буде представляти рішення завдання, отримане за допомогою мурашиного алгоритму.
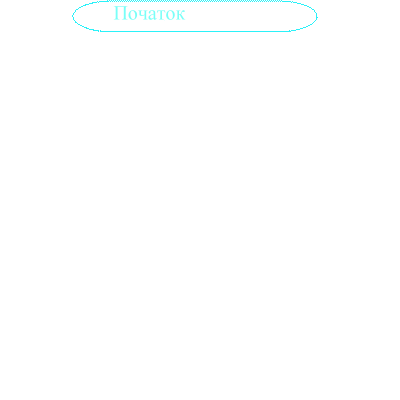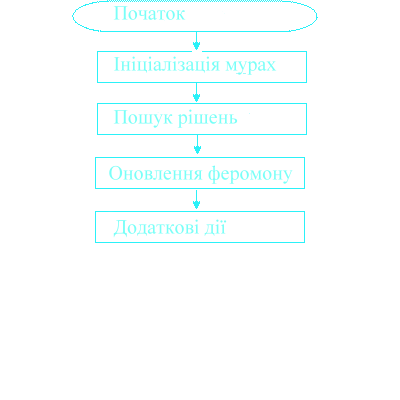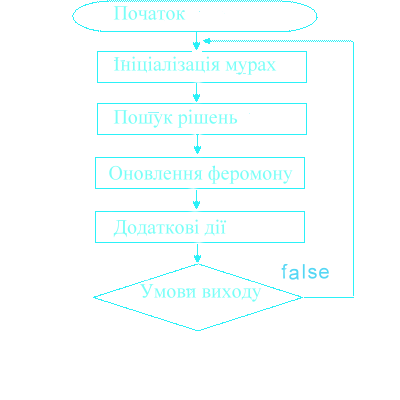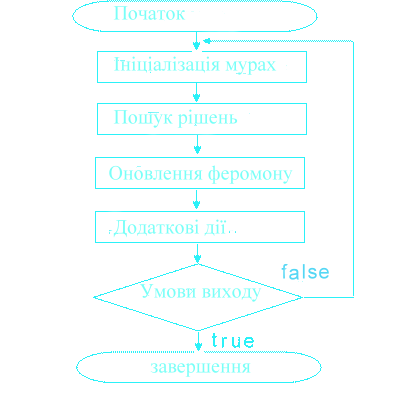
Базовий мурашиний алгоритм, незалежно від модифікацій, можна представити у вигляді схеми (Рисунок 2)


Ініціалізація мурашок - стартова точка, куди вміщується мураха, залежить від обмежень, накладених умовами завдання. Тому що для кожного завдання спосіб розміщення мурашок є визначальним. Або всі вони поміщаються в одну точку, або в різні з повтореннями, або без повторень. На цьому ж етапі задається початковий рівень феромону. Він ініціалізується невеликим позитивним числом для того, щоб на початковому кроці ймовірності переходу в наступну вершину не були нульовими.
Імовірність переходу з вершини i у вершину j визначається згідно формули 1:

(1)

де представляє безліч можливих вершин, пов"язаних з вершиною i, для мурашки k, τ (ij)- рівень феромону, d(ij) – евристична відстань, α та β – константні параметри. Оновлення феромона відбувається відповідно до формули 2.

(2)

де n(k) – кількість мурах, ρ– інтенсивність випаровування, Lk(t) – довжина шляху, побудованого k-ою мурахою в момент часу t, а Q - параметр значущості, тобто – феромон, що відкладався k-ою мурахою, що використовують ребро (i, j)
Для того щоб побудувати відповідний мурашиний алгоритм для розв'язання завдання, необхідно:
1. представити завдання у вигляді набору компонент і переходів або набором неорієнтованих зважених графів, на яких мурашки можуть будувати рішення;
2. визначити значення сліду феромона;
3. визначити евристики поведінки мурашки, коли будуємо рішення;
4. якщо можливо, то реалізувати ефективний локальний пошук;
5. вибрати специфічний мурашиний алгоритм і застосувати для розв'язання задачі;
6. налаштувати параметри алгоритму. [3]
Оскільки в основі мурашиного алгоритму лежить моделювання пересування мурашок по деяких шляхах графа, то такий підхід є ефективним способом пошуку раціональних рішень для задач оптимізації, у першу чергу, на графах.
Розглянемо алгоритм кластеризації зображення, заснований на алгоритмі мурашиних колоній. У цьому алгоритмі мурашки представляються простими агентами, які випадковим чином переміщаються по дискретному масиву. Піксели, які розсіяні в елементах масиву можуть бути переміщені з одного елемента масиву в інший, формуючи кластери. Переміщення пікселів непрямим чином визначається поведінкою мурашок. Кожна мураха може приєднувати або виключати піксел згідно функції, яка обчислює схожість пікселя з іншими пікселями в кластері. Таким чином, мурашки динамічно кластерізірують зображення на незалежні кластери, які включають тільки схожі між собою пікселі. Крім цього агент представляє нові імовірнісні правила для приєднання або виключення пікселів, а так само стратегію локального переміщення для прискорення збіжності алгоритму.
Припустимо, розмірність масиву дорівнює N. Кожен елемент цього масиву пов"язаний з гніздом мурашок в певному порядку, що дозволяє мурашкам легко переходити від одного елемента до іншого. У процесі алгоритму мурахи можуть змінювати, будувати або прибирати існуючі кластери пікселів. Кластер представляється сполученням двох або більше пікселів і розташований в окремій клітинці масиву, що спрощує його ідентифікацію.
Ініціалізуємо N пікселів {Р1,..., Рn}для кластеризації, розташовані в масиві таким чином, що кожен елемент масиву пов"язаний лише з одним пікселом. Кожен мураха а(i) з колонії з К мурахами {a(1)..., а(k)} приєднує випадково обраний піксел з елементів масиву і повертається в гніздо.
Після початкового етапу ініціалізації відбувається етап кластеризації. Вибір мурашки проводиться випадковим чином. Вона переміщається від свого гнізда до елементів масиву і визначає з допомогою імовірнісного правила, чи приєднувати цей піксель до кластера. Кожен мураха знає список розташування пікселів, які не були приєднані іншими мурашками. Випадковим чином мураха визначає наступний піксель зі списку вільних. Цей алгоритм повторюється для кожного мурашки. Алгоритм зупиняється при проходженні заданої кількості ітерацій.
Сама постановка задачі не є чіткою. Як оцінити апріорне уявлення користувача про відокремлення об'єктів? У автоматичній сегментації, для побудови міри якості розбиття, використовуються припущення про те, що подібність (схожість) кольору пікселів, текстури усередині одного об'єкта повинна бути максимальною, а між об'єктами - мінімальною. У інтерактивній сегментації користувач може додавати нові обмеження, уточнювати вхідну інформацію до тих пір, поки не отримає очікуваний результат. Можна було б оцінювати якість сегментації за одних і тих же підказках, але різні алгоритми отримують різну вхідну інформацію від користувача. В інтерактивній сегментації також передбачається, що користувач за допомогою «підказок» алгоритму, повинен мати можливість сегментувати об'єкт навіть у тих випадках, коли його частину і за кольором і за текстурою ближче фону, ніж решті об'єкта. Це теж ускладнює створення об'єктивних метрик. Тому природньо, що для порівняння алгоритмів інтерактивної сегментації найчастіше використовують суб'єктивне порівняння: береться кілька зображень, і декільком користувачам ставиться одна з 2 завдань:
• сегментувати даним алгоритмом всі зображення не гірше заданого рівня (порівняння на «не гірше» здійснюється суб'єктивно самими користувачами, для порівняння дається якийсь зразок сегментації). Після чого визначається найшвидший алгоритм;
• за заданий обмежений час, як можна краще виконати сегментацію даних зображень. Після закінчення встановленого терміну, користувач суб'єктивно оцінює, який алгоритм дав кращу сегментацію.
Для грубої оцінки якості методу в конкретній задачі зазвичай фіксують кілька властивостей, якими повинна володіти хороша сегментація. Якість роботи методу оцінюється в залежності від того, наскільки отримана сегментація володіє цими властивостями. Найбільш часто використовуються наступні властивості:
• однорідність регіонів (однорідність кольору або текстури);
• несхожість сусідніх регіонів;
• гладкість межі регіону;
• маленька кількість дрібних «дірок» всередині регіону.[8]
Хоча алгоритми обробки зображень можуть забезпечити одержання точних кількісних показників (наприклад, вимір фракції викиду лівого шлуночка серця по динамічної послідовності зображень) або можуть вирішувати деякі завдання, які нездійсненні за ручної обробки (наприклад, точна реєстрація мультимодальних зображень), проблеми надійності та відповідальності залишаються головними перешкодами на шляху широкомасштабного використання цих алгоритмів.Перевірка правильності алгоритму часто буває складна через відсутність теорії, що дозволяє кількісно порівнювати результати обробки. [7]