Вступ

1. Актуальність теми

2. Зв'язок роботи з науковими програмами, планами, темами

3. Передбачувана наукова новизна

4. Практичне значення отриманих результатів

5. Огляд досліджень і розробок по темі

6. Мета і завдання розробки і дослідження

7. Рішення завдань і результати дослідження

Висновок

Список літератури

Сільське господарство – галузь господарства, спрямована на забезпечення населення продовольством і одержання сировини для ряду галузей промисловості. Ця галузь є однією з найважливіших, представлена практично у всіх країнах. Найбільш високий рівень сільське господарство досягло в розвинених країнах Європи й Північної Америки, що вступили в постіндустріальну стадію. У цих країнах сільське господарство характеризується науково-обґрунтованою організацією, підвищенням продуктивності, застосуванням нових технологій, систем сільськогосподарських машин, пестицидів і мінеральних добрив, використанням генної інженерії й біотехнології, робототехніки й електроніки, тобто розвивається по інтенсивному шляхові. У веденні фінансово-господарчої діяльності аграрних підприємств у цих країнах для зменшення ризику використовуються системи підтримки прийняття розв'язків. Основними функціями даної системи є:

- прогнозування найвищої вартості даного сільськогосподарського продукту або культури на основі часових рядів;

- ефективне довгострокове планування засівання сільськогосподарських культур.

Актуальність розробки інтелектуальної системи підтримки прийняття рішень у веденні фінансово-господарської діяльності в тому що вона суттєво підвищить ефективність аграрного підприємства на ринку й зменшить ризик прийняття фінансово-господарчих рішень.

Кваліфікаційна робота магістра виконувалася протягом 2009-2010 рр. відповідно до наукових напрямків кафедри "Автоматизовані системи управління" Донецького національного технічного університету.

У країнах СНД керівництво аграрних підприємств не надають значення системам підтримки прийняття рішень. Унаслідок відсутності таких вітчизняних програмних пакетів спеціалізованих на сільськім господарстві й високою вартістю закордонних екземплярів доводиться опиратися на свій досвід і сподіватися на прихильність долі. Ефективність же даних систем доведена більш високим рівнем розвитку закордонних сільськогосподарських підприємств

Основним завданням такої системи є короткострокове й довгострокове планування, для здійснення якого існує безліч загальновизнаних моделей і методів прогнозування тимчасових рядів, які можна розділити на 3 основні групи: эконометричні, регресійні й методи Боксу-Дженкинса. Однак ці методи відрізняються малою ефективністю, незручністю застосування й крайньою негнучкістю. Наукова новизна полягає в створенні оптимального алгоритму, для розв'язку поставленого завдання.

У результаті виконання кваліфікаційної роботи магістра буде створена система підтримки прийняття рішень у веденні фінансово-господарчої діяльності аграрного підприємства, для розробки якої будуть використовуватися найбільш ефективні сучасні алгоритми й методи, за допомогою яких можна здійснювати короткострокове й довгострокове прогнозування, на основі набору факторів, що впливають на ціноутворення сільськогосподарської продукції.

За результатами пошуку серед матеріалів порталу магістрів ДОННТУ були знайдені роботи схожі по розв'язуваних завданнях і обраним методам їх розв'язку, однак серед них немає з аналогічною областю застосування. Їх розробили Солодуха О.В., Гриценко А.В., Гуржий Д.А., Філатова А.Ю., Кириченко Л.М., Столяр А.І., Макеєнко Р.І.

Хоча в Україні не були розроблені системи підтримки прийняття розв'язків для сільськогосподарських підприємств, більш узагальненим аналізом використання нейронних мереж для прогнозування займається безліч фахівців, серед яких особлива увага заслужили кандидати наук України Григоренко Д.П. і Матвійчук А.В.

За рубежем розробці інструментальних засобів для зменшення ризику ведення фінансово-господарчої діяльності аграрних підприємств приділяється багато уваги й цим питанням займаються такі компанії як Unitas Software Ltd, Paloalto Software і ін.

Ціль роботи полягає в розробці комп'ютерної підсистеми підтримки прийняття рішень у веденні фінансово-господарської діяльності за допомогою нейронних мереж і генетичних алгоритмів. Для цього необхідно:

- виділити фактори, що впливають на ціну сільськогосподарської продукції;

- проаналізувавши їх відкинути ті, що мають найменший вплив на систему;

- проаналізувати подібні з розроблювальною системою програмні продукти;

- проаналізувати існуючі топології нейронних мереж, методи їх навчання й ін., вибрати найбільш підходящі з них для даного завдання.

Для розробки нейронної мережі, яка буде прогнозувати фінансово-господарчі показники, вирішені такі завдання: вибір вхідних і вихідних даних, топології мережі, методу навчання нейронної мережі, активаційної функції. Тимчасового ряду динаміки цін буде досить, щоб зробити точний прогноз. Він розбитий на три безлічі: навчальну, тестову й контрольну вибірки, які подаються на входи мережі.

Предобробка даних є важливим кроком при застосуванні нейросетей , які навчаются із учителем, і визначає швидкість навчання, величини помилок навчання й узагальнення й інші властивості мережі. Для предобробки кількісних величин найчастіше застосовують лінійне зрушення інтервалу значення ознаки, наприклад, в інтервал [-1,1]. Формула перерахування значення ознаки x для i- го прикладу вибірки в інтервал [a,b] така:

де x_min , x_max- мінімальне й максимальне вибіркові значення ознаки. При відсутності твердих обмежень на діапазон значень ознаки, які були предоброблені, може бути виконане масштабування, що дає нульове середнє й одиничну дисперсію предобробленої величині, по формулі:

де M(x),σ(x) - вихідне вибіркове середнє й середнє квадратичне відхилення. Одержання нульових середніх для вхідних сигналів мережі прискорює градієнтне навчання, оскільки знижує відношення максимального й мінімального ненульового власних чисел матриці других похідних цільової функції по параметрах мережі.[1]

У якості топології даної нейронної мережі запропонований багатошаровий персептрон, тому що він у середньому показує найкращі результати в завданнях прогнозування часових рядів.

У цій топології нейрони регулярним образом організовані в шари. Вхідний шар, що полягає із чутливих (сенсорних) S- Елементів, на який надходять вхідні сигнали Хi, ніякої обробки інформації не робить і виконує лише розподільні функції. Кожний S- Елемент пов'язаний із сукупністю асоціативних елементів ( А-Елементів) першого проміжного шару, а А- Елементи останнього шару з'єднані з реагуючими елементами ( R-Елементами).

Малюнок 1. Структура багатошарового персептрона (Анімація: 5 кадрів, затримка 0,4 сек, розмір 28,6 Кб)

Зважені комбінації виходів R- Елементів становлять реакцію системи, яка вказує на приналежність розпізнаваного об'єкта певному образу. Якщо розпізнаються тільки два образи, то в персептроні встановлюється один R- Елемент, який має дві реакції – позитивну й негативну. Якщо образів більше двох, то для кожного образу встановлюють свій R- Елемент, а вихід кожного такого елемента представляє лінійну комбінацію виходів A- Елементів. [2]

У якості методу навчання нейтронної мережі був обраний метод зворотного поширення помилки. Основна ідея зворотного поширення полягає в тому, щоб одержати оцінку помилки для нейронів схованих шарів. Помітимо, що відомі помилки, що робляться нейронами вихідного шару, виникають внаслідок невідомих поки помилок нейронів схованих шарів. Чим більше значення синаптичного зв'язку між нейроном схованого шару й вихідним нейроном, тем сильніше помилка першого впливає на помилку другого. Отже, оцінку помилки елементів схованих шарів можна одержати, як зважену суму помилок наступних шарів. При навчанні інформація поширюється від нижчих шарів ієрархії до вищих, а оцінки помилок, що робляться мережею – у зворотному напрямку [3].

На етапі навчання відбувається обчислення синаптичних коефіцієнтів w. При цьому на відміну від класичних методів в основі лежать не аналітичні обчислення, а методи навчання по зразках за допомогою прикладів згрупованих у навчальній виборці. Для кожного образу з навчальної вибірки вважається відомим необхідне значення виходу нейронної мережі. Цей процес можна розглядати як розв'язок завдання оптимізації. Її метою є мінімізації функції помилки або не в'язання Е на навчальній виборці шляхом вибору значень синоптичних коефіцієнтів w.

де d_i - необхідне (бажане) значення виходу на j- му зразку вибірки;

y_i - реальне значення;

p - число зразків навчальної вибірки.

Мінімізація помилки Е звичайно здійснюється за допомогою градієнтних методів. Зміна ваг відбувається в напрямку зворотному напрямку найбільшої крутості функції помилки.

де 0 < &eta &le 1 - обумовлений користувачем параметр.

Існує два підходи до навчання. У першому з них ваги w перераховуються після подачі усій навчальної вибірки, і помилка має вигляд

У другому підході помилка перераховується після кожного зразка:

Нехай

, тобто

Тоді

, де y_j(S_j) - активаційна функція. Для

Третій співмножник:

Можна показати, що

при цьому підсумовування k іде серед нейронів n- го шару. Введемо нове позначення:

Для внутрішнього нейрона:

Для зовнішнього нейрона:

Таким чином, повний алгоритм навчання зворотного поширення будується так:

1. Подати на входи мережі один з можливих зразків у режимі звичайного функціонування НС, коли сигнали поширюються від входу до виходів розрахувати значення виходів усіх нейронів (звичайно початкове значення ваги становлять малі значення).

2. Розрахувати значення &delta _jⁿ для нейронів вихідного шару по формулі (13)

3. Розрахувати значення &delta _jⁿ для всіх внутрішніх нейронів по формулі (12)

4. За допомогою формули (14) для всіх зв'язків знайти збільшення вагових коефіцієнтів &Delta W _jⁿ.

5. Скорегувати синаптичні ваги:

6. Повторити кроки 1-5 для кожного образа навчальної вибірки поки помилка Е не стане досить маленької.

У якості активаційної функції вхідного й вихідного шару обрана лінійна функція.

Нейрони схованих шарів будуть активуватися за допомогою раціональної сигмоїдальної функції.

Ефективність даного варіанта визначається тим, що дана функція є строго монотонно зростаючої, безперервної та дифференцируємою і на обчислення раціональної сигмоїди в порівнянні з іншими затрачається менше процесорного часу.

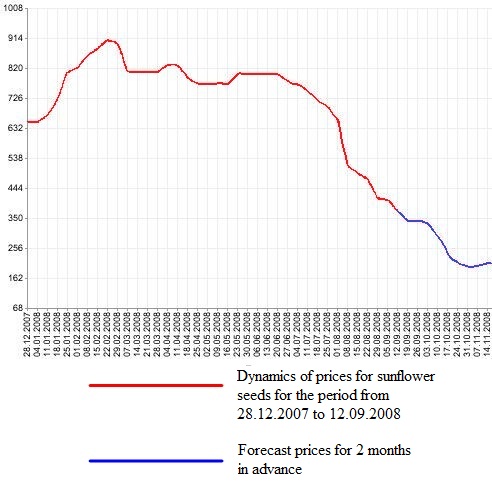Малюнок 2. Графік прогнозування тимчасового ряду

Після вибору загальної структури потрібно експериментально підібрати параметри мережі. Для мережі необхідно підібрати число шарів і кількість нейронів у кожному з них. При виборі кількості шарів і нейронів у них слід виходити з того, що здатності мережі тем вище, чим більше сумарне число зв'язків між нейронами. З іншого боку, число зв'язків обмежене зверху кількістю записів у навчальних даних.

Опираючись на результати, отримані експериментальним шляхом, у результаті реалізації запропонованої нейтронної мережі в пакеті Matlab, ми бачимо, що дана топологія нейронної мережі й метод її навчання є вкрай ефективним у завданнях прогнозування.

Ефективна діяльність підприємств у значній мірі залежить від того, наскільки вірогідно вони передбачать далеку й близьку перспективу свого розвитку, тобто від прогнозування. На даний момент найефективнішим інструментом прогнозування є штучні нейронні мережі. У статті були розглянуті топологія штучної нейронної мережі, метод її навчання, вхідні дані, їх предобробка й інші характеристики нейтронної мережі для прогнозування фінансово-господарчих показників сільськогосподарського підприємства; виділені основні завдання, які необхідно виконати для її розробки.

1. Гитис В.Б. Сопряжение информационных потоков нейросетевой системы нормирования времени механообработки деталей // «Искусственный интеллект». – 2005 №3. С.285

2. Шитиков В.К., Розенберг Г.С., Зинченко Т.Д. Нейросетевое моделирование [http://www.ievbran.ru/kiril/Library/Book1/content394/content394.htm].

3. Бакаев В.Н., Владимирова Н.В., Васильева Е.Ю. Методы обучения нейросистем [http://zdo.vstu.edu.ru/umk/html/manual/L5_6.html] // Хрестоматия по курсу "Моделирование систем", Вологодский Государственный Технический университет.

4. Солдатова О.П., Семенов В.В. Применение нейронных сетей для решения задач прогнозирования [http://zhurnal.gpi.ru/articles/2006/136.pdf] // Электронный научный журнал «Исследовано в России»

5. Иванов М.Н. Анализ роста курса акций с применением нейронных сетей. // Труды VIII Всероссийской конференции «Нейрокомпьютеры и их применение». – 2002. С.756-772.

6. Ибираимова Т.Б. Прогнозирование тенденций финансовых рынков с помощью нейронных сетей // Труды VIII Всероссийской конференции "Нейрокомпьютеры и их применение " – 2007. С. 745-755.

7. Крисилов В.А. Чумичкин К.В. Кондратюк А.В. Представление исходных данных в задачах нейросетевого прогнозирования // Конференция "Нейроинформатика 2003". – М.: НАУЧНАЯ СЕССИЯ МИФИ, 2003. С 184-191