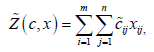
Source of information: http://www.kmi.kherson.ua/downloads/isdmit2005_4.pdf
Однією з важливих проблем на морському транспорті є проблема планування ефективних маршрутів суден на основі мінімізації їх подовженості, зниження часової тривалості та витрат палива на їх реалізацію.
Розв’язок задач такого класу суттєво ускладнюється при необхідності врахування широкого спектру факторів та збурюючих впливів, характерних для морського середовища. Особлива увага проблемі оптимізації маршрутів приділяється при плануванні маршрутів суден в умовах невизначеності. Джерелами невизначеності в умовах реального морського середовища є ситуації, при яких: а) апріорно невідома кількість портів (точок заходу судна), які мають знаходитись на маршруті; б) відсутня інформація про послідовність заходів судна в ті чи інші порти на маршруті; в) розмитою або нечіткою є інформація про кількість вантажу, який має бути розвантажений в кожному з портів на маршруті; г) відстані між портами, залишаючись постійними величинами на етапі планування маршрутів, можуть суттєво відрізнятись від запланованих через зміну погодних умов та необхідність дотримання вимог безпеки мореплавства, наприклад, в передштормових чи штормових умовах; д) в процесі здійснення попередньо запланованого маршруту може виникати необхідність включення до маршруту додаткових точок заходу судна; е) в процесі реалізації маршруту можуть виникати пошкодження в різних суднових системах та корпусі судна або аварійні ситуації, що пов'язані з зіткненням суден у вузькостях та протоках, висадкою на мілину тощо.
Як приклади ефективного застосування методів дослідження операцій [1] для синтезу алгоритмів прийняття рішень в умовах нестаціонарного морського середовища слід назвати успішні розв’язки задач [2] ресурсного менеджменту для торгового флоту, планування розкладу ескадри суден берегової охорони США, пошуку консенсусу при централізації та децентралізації прийняття рішень для великої групи суден, моделювання реального середовища для дослідження суднових екстремальних ситуацій в умовах вузькостей водного шляху, прийняття рішень в аварійних ситуаціях при виникненні пошкоджень суднового обладнання у відкритому морі та ін. В роботі [3] сформовано математичну модель як задачу математичного програмування для оптимізації маршрутів чартерних суден-контейнеревозів, в [4] запропонована модель і алгоритм для планування морських транспортних перевезень, зокрема для формування проблеми розкладу руху суден компанії Kuwait Petroleum Corporation при проектуванні оптимальних маршрутів танкерів.
В даній доповіді розглядаються алгоритмічні підходи та математична формалізація задач планування та оптимізації маршрутів суден в умовах реального морського середовища, яке може створювати високодинамічні екстремальні умови, а ступінь нечіткості (розмитості) параметрів та характеристик такого середовища є досить високою. Для формалізації багатьох процесів, об’єктів і систем, що функціонують в умовах невизначеності, широке застосування знаходять методи інтелектуальної підтримки рішень на основі теорії нечітких множин та нечіткої логіки [5,6], зокрема в задачах управління суднами, підводними апаратами та роботами, маніпуляційними системами з рухомою основою [2,7] та ін.
Особлива увага приділяється плануванню маршрутів морських танкерів,
які здійснюють бункерування (завантаження паливом) інших суден. При цьому
судна-замовники можуть знаходитись в різних портах морської акваторії, що
обслуговується відповідною морською бункерувальною компанією чи
декількома бункерувальними компаніями. Планування маршрутів танкерів є
задачею проектування оптимальних маршрутів в умовах невизначеності [2].
Так, наприклад: а) довжина ij -го шляху, тобто відстань lij між i-м та j-м
портом може змінюватись в процесі реалізації маршруту танкера при
несприятливих погодних умовах; б) в цільових функціях Z(c, x) , що
вибираються для оптимізації морських транспортних перевезень (транспортні
задачі)
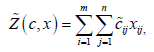
кожний вартісний коефіцієнт 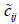 , в загальному випадку, є нечіткою множиною,
(де xij - кількість вантажу, що транспортується від порта i до порту j). Зокрема,
нечіткий характер параметра
, в загальному випадку, є нечіткою множиною,
(де xij - кількість вантажу, що транспортується від порта i до порту j). Зокрема,
нечіткий характер параметра 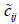 цільової функції Z(c, x) , що забезпечує
мінімізацію загальних витрат на реалізацію маршруту танкера, залежить від
цілого ряду факторів. Перш за все це пов’язано з тим, що значення кожного
коефіцієнта
цільової функції Z(c, x) , що забезпечує
мінімізацію загальних витрат на реалізацію маршруту танкера, залежить від
цілого ряду факторів. Перш за все це пов’язано з тим, що значення кожного
коефіцієнта 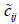 залежить від витрат на перевезення вантажу, витрат на
розвантаження вантажу, а також витрат на забезпечення безпечного
проведення операцій (наприклад, при бункеруванні суден) та на дотримання
вимог екологічної служби даного морського регіону , а також від інших
компонентів, наприклад, портових санітарних (платіжних) зборів або зборів за
послуги митної служби, що можуть бути включені в одну з вищевказаних
компонент.
залежить від витрат на перевезення вантажу, витрат на
розвантаження вантажу, а також витрат на забезпечення безпечного
проведення операцій (наприклад, при бункеруванні суден) та на дотримання
вимог екологічної служби даного морського регіону , а також від інших
компонентів, наприклад, портових санітарних (платіжних) зборів або зборів за
послуги митної служби, що можуть бути включені в одну з вищевказаних
компонент.
Детально аналізуються загальні фактори, що впливають на формування
нечітких значень коефцієнтів ij c% і приводять задачу планування маршрутів суден
до оптимізаційної задачі, що має розв’язуватись в умовах невизначеності при
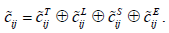
Зокрема, відстань між i-м портом, з якого танкер виходить, та j-м портом,
до якого танкер прямує, визначає значення компоненти 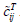 . Ступінь нечіткості
цієї компоненти є найбільш високим, оскільки залежить в значній мірі від
погодних умов в регіоні: а) якщо погодні умови є сприятливими, то судноводій
(при відсутності перешкод) вибирає традиційний найкоротший шлях з
урахуванням вимог відповідного Регістру судноплавства; б) якщо погода
відповідно до поточного метрологічного прогнозу має тенденцію до змін в
напрямку штормового стану , то судноводій може вибрати інший (з точки зору
безпеки судна) шлях, який, як правило, буде довшим ніж традиційний шлях.
Нова траєкторія руху судна має бути сформована з урахуванням особливостей
даного морського регіону (бухти, мілини, перешкоди, роза вітрів тощо). Сила і
напрям вітру та морська течія, що мають зазвичай змінний характер, також
впливають на реальні значення параметру cijT, збільшуючи або зменшуючи його
по відношенню до значення
. Ступінь нечіткості
цієї компоненти є найбільш високим, оскільки залежить в значній мірі від
погодних умов в регіоні: а) якщо погодні умови є сприятливими, то судноводій
(при відсутності перешкод) вибирає традиційний найкоротший шлях з
урахуванням вимог відповідного Регістру судноплавства; б) якщо погода
відповідно до поточного метрологічного прогнозу має тенденцію до змін в
напрямку штормового стану , то судноводій може вибрати інший (з точки зору
безпеки судна) шлях, який, як правило, буде довшим ніж традиційний шлях.
Нова траєкторія руху судна має бути сформована з урахуванням особливостей
даного морського регіону (бухти, мілини, перешкоди, роза вітрів тощо). Сила і
напрям вітру та морська течія, що мають зазвичай змінний характер, також
впливають на реальні значення параметру cijT, збільшуючи або зменшуючи його
по відношенню до значення 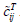 .
.
Розглянуті нечіткі параметри cij, як і нечіткі замовлення xj портів (суден-
замовників), для планування бункерувальних операцій доцільно моделювати з
використанням функцій належності трикутної та LR-форми у вигляді нечітких
множин [5,6]

Для організації бункерувальних операцій з нечіткими замовленнями в
портах в доповіді обговорюються наступні складові алгоритму планування та
оптимізації маршрутів танкерів в умовах невизначеності, зокрема [2]:
– аналіз вхідних даних для танкерів-бункерувальників: вантажомісткість
(D), нечіткі значення замовлень портів xj, відстані між портами;
– синтез функцій належності нечітких замовлень портів;
– формування математичної моделі для оптимізації маршрутів суден, як
задачі цілочисельного програмування, з урахуванням обмежень на загальну
кількість розвантаженого вантажу;
– розв’язок задачі математичного програмування з урахуванням
наступних вимог: а) сумарна довжина маршрутів має бути мінімізованою; б)
танкер на маршруті заходить в будь-який порт тільки один раз; в) початком і
кінцем кожного маршруту є початковий порт; г) замовлення кожного з портів
має бути виконаним;
– аналіз кількості визначених маршрутів, оцінка можливості проведення
всіх бункерувальних операцій в зазначений період часу;
– оцінка ефективності E0i проведення бункерувальних операцій на
кожному i – му маршруті за критерієм
 де Di - кількість нереалізованого на i-му маршруті вантажу, що залишилась
на танкері при поверненні його в початковий порт;
де Di - кількість нереалізованого на i-му маршруті вантажу, що залишилась
на танкері при поверненні його в початковий порт;
– оцінка ефективності E0 проведення бункерувальних операцій на
всіх r маршрутах
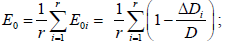 – аналіз результатів планування бункерувальних операцій.
– аналіз результатів планування бункерувальних операцій.
В доповіді також обговорюються результати моделювання процесів
планування та оптимізації маршрутів для різних бункерувальних програм і
різних нечітких моделей замовлень портів [8,9]. Зокрема для випадку
обслуговування 12 портів при імітаційному моделюванні трьох варіантів
комплексних реальних замовлень наведено результати аналізу рівня
ефективності E0, пов’язаного з визначенням ступеню розвантаження кожного
танкера на відповідному маршруті. При цьому для кожного з трьох варіантів
отримано: E01 =0,659; E02 =0,6484; E03 =0,74. Тобто для 3-го варіанта, враховуючи
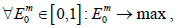 попередньо спланована стратегія реалізації маршрутів є найбільш ефективною.
попередньо спланована стратегія реалізації маршрутів є найбільш ефективною.
Умови невизначеності, що мають бути враховані при оптимізації маршрутів суден, суттєво впливають на вибір тих чи інших алгоритмів оптимізації. Разом з тим, саме застосування теорії нечітких множин дозволяє успішно формалізувати задачі такого класу, а більш того, використання нечіткої логіки дає змогу розробляти нечіткі експертні системи [8], що забезпечують ефективне планування, оптимізацію та коригування маршрутів в off-line та on-line режимах.