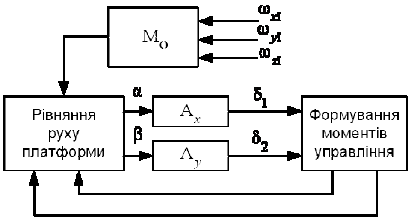
Рис. 1. Структурна схема математичної моделі системи визначення курсу в режимі попереднього приведення до горизонту (Ax, Ay – акселерометри; Мо – момент опору)
Source of information: http://www.kmi.kherson.ua/downloads/isdmit2005_4.pdf
У наш час гіроскопічним системам визначення курсу приділяється значна увага. Це зумовлюється необхідністю одержання безперервної та точної інформації про курс під час розв’язання задач точної та надійної навігації. Найбільше поширення мають системи визначення курсу, які можуть використовуватись як гірокомпаси і як гіроазимути.
Ускладнення рухомих об’єктів, підвищення інтенсивності перевезень водним транспортом зумовлюють актуальність проектування якісних навігаційних систем із розширеними функціональними можливостями. Останньою тенденцією проектування навігаційних приладів є створення систем, що об’єднують у собі гірокомпас та гіровертикаль, а також забезпечують визначення інформації про лінійну швидкість об’єкта. За своїми функціональними можливостями такі системи наближаються до інерціальних навігаційних систем, але відрізняються від них значно нижчою вартістю.
Успішність проектування навігаційної системи значною мірою визначається на початкових етапах проектування. При цьому проектувальник системи має володіти інструментом, який дозволяє йому приймати оптимальні рішення за умов відсутності реально існуючого зразка системи. Таким інструментом є моделювання системи. Отже, різні аспекти створення моделей систем водного транспорту є важливим моментом, який дозволяє досягти успіхів у створенні системи та її подальшій експлуатації.
Особливості моделювання систем визначення просторової орієнтації рухомих об’єктів достатньо широко висвітлені у літературі, наприклад в працях [1, 2, 3], але при цьому не робиться акцент на моделюванні окремих режимах їхньої роботи, в той час як характерною рисою сучасних навігаційних систем є наявність значної кількості різних режимів, що характеризуються різним складом пристроїв і відповідно різними особливостями та умовами моделювання. Важливій вплив на моделювання таких систем має урахування руху основи, тобто платформи, на якій встановлюються навігаційні пристрої.
У роботі розглядається платформна система визначення курсу до складу якої входять два гіроскопи із динамічним настроюванням, що виконують функції гіровертикалі і вимірювача курсу, а також акселерометри, за допомогою яких здійснюється корекція гіроскопів. Стабілізація платформи здійснюється за сигналами гіроскопа із динамічним настроюванням, що виконує функції гіровертикалі. Визначення курсу або гіроазимуту залежно від зовнішньої команди здійснюється за допомогою гіроскопу із динамічним настроюванням, що виконує функції вимірювача курсу.
Така система являє собою складний прилад, що працює в багатьох режимах, а саме: попереднього приведення до горизонту, точного приведення до горизонту, визначення курсу та визначення азимуту. Кожний з цих режимів характеризується своїм складом пристроїв та своїми умовами роботи. Отже, математична модель має враховувати особливості того чи іншого режиму. Якщо йдеться про режим попереднього приведення до горизонту, то його модель має включати моделі платформи та акселерометрів. Модель, що відповідає режиму точного приведення до горизонту, має включати моделі платформи, акселерометрів та гіроскопа, що виконує функції гіровертикалі. І, нарешті, модель режимів визначення курсу та гіроазимуту має враховувати моделі платформи, акселерометрів, та гіроскопу, що виконує функції вимірювача курсу. Слід зазначити, що обов’язковою умовою якісного моделювання є урахування в моделях різних режимів системи визначення курсу руху платформи, на якій встановлюються пристрої вимірювання навігаційних параметрів.
Структурна схема математичної моделі системи визначення курсу в режимі попереднього приведення до горизонту, яка складається з динамічних та кінематичних рівнянь платформи та рівнянь акселерометрів, представлена на рис. 1.

Математична модель системи визначення курсу в режимі попереднього
приведення до горизонту має вигляд:

де Jx, Jy, Jz – осьові моменти інерції платформи; fx ,fy ,fz – моменти в’язкого тертя; Мo – момент опору стабілізуючих двигунів; w0 – зовнішня кутова швидкість, що діє на платформу; a, b, g – кути поворотів платформи відносно поздовжньої, вертикальної та бічної осей рухомого об’єкта відповідно; k1, k2, k3, k4, k5 – коефіцієнти передачі; d1, d2 – вихідні сигнали акселерометрів; T – стала часу акселерометрів.
Структурна схема математичної моделі системи визначення курсу в режимі точного приведення до горизонту, яка складається з динамічних та кінематичних рівнянь платформи, рівнянь гіроскопів із динамічним настроюванням та рівнянь акселерометрів, представлена на рис. 2.

З урахуванням вищезгаданого математична модель системи визначення
курсу в режимі точного приведення до горизонту приймає вигляд:
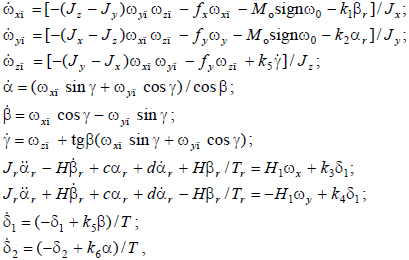
де k1, k2, k3, k4, k5, k6 – коефіцієнти передачі; Ar, Br – кути відхилення гіроскопу із динамічним настроюванням, що виконує функції гіровертикалі; Jr – сумарний момент інерції гіроскопа; H – кінетичний момент гіроскопа; c – остаточна жорсткість карданового підвісу гіроскопа; d – коефіцієнт демпфірування; H1 = H(1 - s) , де s =10-3 ; Tr – стала часу прецесії.
Моделі в режимах визначення курсу та азимуту відрізняються від наведеної моделі тим, що до її складу входить гіроскоп, що виконує функції вимірювача курсу. Отже, відповідно змінюються рівняння руху гіроскопа із динамічним настроюванням. Крім того під час моделювання необхідно враховувати, що кожний режим відрізняється особливостями управління, які детально описуються в працях [5, 6].
Запропоновано математичну моделі системи визначення курсу в режимах попереднього приведення до горизонту, точного приведення до горизонту та визначення курсу/азимуту з урахуванням руху основи (платформи), що дає можливість вже на початкових етапах проектування приймати заходи по створенню якісної системи визначення навігаційних параметрів рухомих об’єктів водного транспорту.