Построение зоны навигационной безопасности объекта и его кинематических характеристик на основе обсервации двух разнесенных точек объекта
С.В. Пашенцев
Судоводительский факультет МГТУ, кафедра судовождения
Source of information: http://vestnik.mstu.edu.ru/v03_1_n06/articles/03_pash.zip
Аннотация
В работе рассмотрена возможность построения зоны навигационной безопасности подвижного объекта и его кинематических характеристик при обсервации двух его разнесенных точек. Построены точностные характеристики любой точки объекта при известных эллипсах рассеивания обсервованных точек. Навигация, которая может быть основана на подобной информации об объекте, названа автором двухточечной.
Abstract
The possibility of the construction of a navigational safety zone of a mobile vehicle and kinematic characteristics under observation of its two distant points has been considered in the work. The method of observing of coordinates errors of any point of the vehicle, when dispersion ellipses of observation points are known, has been worked out in the paper. Navigation which can be based on this kind of information concerning the vehicle has been called by the author as a two-point navigation.
1. Введение
При значительных размерах подвижных морских объектов, сравнимых с размерами самих акваторий, в которых происходит его маневрирование, в целях безопасности мореплавания необходимо знать положение всех (или нескольких) точек объекта, а не только его центра масс.
Для жесткого тела достаточно знание положения всего двух точек, чтобы затем определять положение любой его точки. Если к тому же получена оценка точности обсервованных точек, то появляется возможность построения ассоциированной с объектом фигуры: зоны навигационной безопасности (ЗНБ).
Кроме того, знание векторов скоростей этих же базовых точек дает возможность полностью рассчитать кинематику объекта и определить такие важные характеристики движения, как вектор путевой скорости, угол дрейфа, мгновенный центр вращения и угловая скорость поворота вокруг него.
При современных средствах определения места с их высокой точностью достаточно иметь обсервации этих двух точек с линейной погрешностью, меньшей на порядок размера базы, т.е. расстояния между двумя обсервованными точками объекта. Навигацию, основанную на описанной выше информации, можно назвать "двухточечной".
2. Построение зоны навигационной безопасности
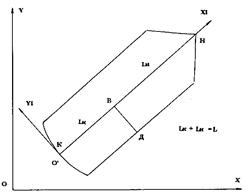
Рассмотрим подвижный объект в некоторой абсолютной системе координат X, Y (рис. 1). Пусть координаты носовой и кормовой точек объекта будут (XН, YН) и (XК, YК) соответственно. Будем считать, что объект снабжен средствами обсервации, позволяющими определить координаты этих двух базовых точек и оценить погрешность такой обсервации с помощью эллипса погрешностей каждой из точек.
|
Рис. 1. Система координат объекта |
Введем далее локальную систему координат, связанную с объектом. Координатная ось X1 направлена вдоль ДП объекта от кормовой точки к носовой, ось Y1 ей перпендикулярна. Попробуем выразить координаты произвольной точки борта Д через координаты носовой и кормовой точек. Пусть точка В – проекция Д на ДП – удалена от кормы и носа на расстояния LК и LН соответственно, так что длина объекта вдоль ДП L = LК + LН. Если ввести отношения a = LК/L и b = LН/L, то легко найти координаты В, как точки, делящей отрезок НК в отношении l = a/b:
XВ = (XН l + XК)/(1+l), YВ = (YН l + YК)/(1+l). (1)
При этом кормовой точке соответствует значение l = 0, а носовой точке – значение l = ¥. Запишем уравнение прямой, которая перпендикулярна ДП в точке В:
Y – YВ = - (X – XВ) / KДП, (2)
учитывая известное соотношение угловых коэффициентов перпендикулярных прямых k1 = -1/k2. Здесь KДП = (YН – YК)/(XН - XК) – угловой коэффициент прямой линии ДП. На этой прямой, в частности, для точки Д, выполняется равенство:
YД – YВ = - (XД – XВ)/KДП. (3)
Квадрат расстояния d вдоль этого перпендикуляра (1) от точки В до точки Д на обводе судна можно найти обычным образом:
d2 = (XВ - XД)2 + (YВ – YД)2,
и с учетом (3):
d2 - (XВ - XД)2 = (XВ - XД)2/KДП2,
или
XВ – XД = ±d (1 + 1/KДП2)1/2,
что приводит, наконец, к выражениям для координат бортовой точки Д объекта:
|
XД = (XК + XН l)/(1 + l) ± d/L (YН – YК), YД = (YК + YН l)/(1 + l) ± d/L (XН – XК) |
(4) |
(с учетом того, что L2 = (XН - XК)2 + (YН - YК)2, а 1 + 1/KДП2 = L/(YН - YК)). При этом двойной знак второго слагаемого определяет координату левого (правого) бортов.
Выведенные выражения для искомых координат линейны относительно полученных при обсервации координат носовой и кормовой точек объекта, и эта линейность позволит легко найти дисперсии этих точек при известных дисперсионных характеристиках точек К и Н. Правда, применить оператор дисперсии к обеим частям равенств (4) сложно, так как отдельные слагаемые правых частей функционально зависимы друг от друга. Действительно, d/L есть функция l, зависящая от формы обводов судна. При взятии дисперсии от правой части пришлось бы учитывать эту связь, а не использовать простое правило – "дисперсия суммы равна сумме дисперсий". Поэтому пойдем другим путем. Возьмем от обеих частей равенств (4) математические ожидания, а затем с их помощью найдем отклонения координат от математических ожиданий.
Математические ожидания координат XД и YД:
|
M(XД) = (M(XК) + M(XН) l)/(1 + l) + d/L (M(YН) – M(YК)), M(YД) = (M(YК) + M(YН) l)/(1 + l) + d/L (M(XН) – M(XК)). |
(5) |
Отклонения координат XД и YД от их математических ожиданий:
|
VХД = XД - М(XД) = (VХН + VХК l)/(1 + l) + d (VYН – VYК), VYД = YД - М(YД) = (VYН + VYК l)/(1 + l) + d (VХН – VХК), |
(6) |
где для простоты последующих записей обозначено d = d/L. Обратим внимание на то, что структура отклонений полностью аналогична структуре самих координат, в силу их линейности, о которой было сказано выше. В соотношениях (5) и (6) и далее дополнительные нижние индексы Д, Н или К означают принадлежность статистической характеристики точке Д, Н или К.
Зная отклонения координат, можно вычислить корреляционный момент между ними, которого нам как раз и не хватало для расчета дисперсий координат. Исходим из определения корреляционного момента как математического ожидания от произведения отклонений:
MXYД = M{[VХК VYК + lVХН VYК + lVХН VYН + l2VХН VYН]/(1+l)2 +
+ d2 [VYН VХН – VYК VХН – VYН VХН + VYК VХН] +
+ d/(1+l) [VХК VХН + lVХНVХН – VХН VХК - lVХН VХК +
+ VYК VYН + l VYН VYН – VYК VYК - l VYН VYК] } =
= (MXYК + l2MXYН)/(1+l)2 + d2 (MXYК + MXYН) + d/(1+l)(lDXН - DXК + lDYН - DYК). (7)
Найдем также квадраты отклонений (6):
VХД 2 = (VХН + VХН l)2/(1+l)2 + d2(VYН – VYК)2+ 2d/(1+l) (VХК + VХН l)(VYН – VYК) =
= (VХК 2 + l2VХН2 + 2lVХК VХН)/ (1+l)2 + d2(VYН 2 + VYК 2 - 2VYК VYН) + (8)
+ 2d/(1+l)(VХК VYН + lVХН VYН - VХК VYК - lVХН VYК).
Применив операцию математического ожидания к обеим частям равенства (8), получаем дисперсии координат:
|
D(XД) = [D(XК)+l2D(XН)]/(1+l)2+d2[D(YК)+D(YН)] + 2d/(1+l)[lMXYН - MXYК], D(YД) = [D(YК)+l2D(YН)]/(1+l)2+d2[D(XК)+D(XН)] + 2d/(1+l)[lMXYН - MXYК]. |
(9) |
Получены все необходимые формулы для формирования эллиптической погрешности точки Д, т.е. определения параметров ее эллипса погрешностей. Для этого воспользуемся известными формулами объединения двух векториальных погрешностей V1 и V2 в эллипс погрешностей (Абезгауз, 1970). Они определяют ориентацию результирующего эллипса – угол a между большой осью эллипса и большей векториальной погрешностью:
tg 2a = (V22 sin2q + 2kV1 V2 sinq)/(V12 + V22 cos2q + 2kV1 V2 cosq). (10)
Две другие формулы вычисляют квадраты полуосей эллипса погрешностей a и b:
a2(b2) = 0.5{(V12 + V22 + 2kV1 V2 cosq) ±
[ (V12 + V22 cos2q + 2kV1 V2 cosq)2 + (V22 sin2q + 2kV1 V2 sinq)2 ]1/2 }. (11)
Здесь k и q - коэффициент корреляции и угол между векториальными погрешностями V1 и V2.
В нашем случае формулы (10), (11) можно упростить, так как векториальные погрешности ортогональны, и угол q = 0. Тогда
tg 2a = 2kV1 V2 / (V12 - V22) (12)
a2(b2) = 0.5{(V12 + V22) + [(V12 - V22)2 + (2kV1 V2)2 ]1/2 }. (13)
Найденные нами выше дисперсии (9) координат точки Д и есть квадраты объединяемых векториальных погрешностей, а корреляционный момент (7) есть произведение коэффициента корреляции и векториальных погрешностей:
MXYД = k V1 V2, D(XД) = V12, D(YД) = V22.
Следовательно, искомые параметры эллипса погрешностей (12), (13) точки Д можно выразить в терминах дисперсий и корреляционного момента в этой точке:
tg 2a = 2MXYД / (D(XД - D(YД))
a2(b2) = 0.5{(D(XД) + D(YД)) + [(D(XД) - D(YД))2 + (2 MXYД)2]1/2 }. (14)
Поскольку приемоиндикаторы профессиональных спутниковых систем навигации определяют, помимо самих координат, параметры стандартного эллипса погрешностей обсервованной точки, то следует выразить именно через них параметры (14) эллипса погрешностей произвольной точки Д обвода корпуса объекта. Обозначим эти параметры обсервованных точек как aк, bк, aк и aн, bн, aн - полуоси эллипса и угол наклона его большой оси для точек К и Н.
Для каждой из этих точек можно записать набор соотношений, хорошо известных из теории эллиптических погрешностей.
MXYК = 0.5 tg2aк [D(XК) – D(YК)] = 0.5
[D(XК) – D(YК)] = cos2aк (aк2 - bк2) (15)
[D(XК) + D(YК)] = (aк2 + bк2).
Аналогичны и формулы для носовой точки Н, достаточно лишь сменить в них всюду "К" на "Н".
Подставив соотношения (15) в выражение (7) для корреляционного момента в точке Д, получим необходимые для расчета комбинации параметров:
2MXYД = (aк2 - bк2) sin2aк[1/(1 + l)2 + d2] + (aн2 – bн2) sin2aн[l2/(1 + l)2 + d2] +
+ 2d/(1 + l)[l (aн2 + bн2) - (aк2 + bк2)],
D(XД) + D(YД) = [l2 (aн2 + bн2) + (aк2 + bк2)]/ (1 + l)2 + d2[(aн2 + bн2) + (aк2 + bк2)] + (16)
+ 2d/(1 + l)[l (aн2 - bн2) sin2aн - (aк2 - bк2) sin2aк],
D(XД) - D(YД) = [1/(1 + l)2 + d2] (aк2 - bк2) cos2aк + [l2/(1 + l)2 + d2] (aн2 – bн2)sin2aн.
Этих трех характеристик достаточно, чтобы, подставив их в формулы (14), определить окончательно параметры эллипса погрешностей, связанного с точкой Д.
3. Пример численного расчета
Приведем пример расчета характеристик эллипса погрешностей для следующего случая (погрешности в метрах, углы в градусах):
Параметры эллипса кормовой точки - aк = 10, bк = 8, aк = 20.
Параметры эллипса носовой точки - aн = 12, bн = 10, aн = 30.
Результаты расчета параметров эллипса для точки Д приведены в таблице для нескольких точек прямолинейного обвода судна при d = 3/20.
Вычислением проверены все формулы, которые в частных случаях точек К(l = 0, d = 0) и Н(l = 100, d = 0) дают характеристики эллипсов погрешностей именно этих точек.
|
lД |
0.5 |
1.0 |
2.0 |
4.0 |
8.0 |
16.0 |
0 |
¥ |
|
aД |
13 |
32 |
36 |
38 |
38 |
39 |
20 |
30 |
|
aД |
8 |
99 |
9 |
10 |
11 |
11 |
10 |
12 |
|
bД |
7 |
6 |
6 |
7 |
7 |
7 |
8 |
10 |
4. Определение кинематических характеристик объекта
|
Рис. 2. Кинематические характеристики объекта |
Будем считать также, что спутниковые приемоиндикаторы, которые используются на объекте, позволяют определять не только координаты точки, но и вектор ее скорости с помощью допплеровского эффекта (а не путем вычисления приращений координат). Итак, пусть известны векторы скоростей носовой VН и кормовой VК точек объекта (рис. 2). Выберем мгновенный центр вращения объекта на его ДП в некоторой точке О*. Вектор поступательной скорости объекта направлен вдоль некоторой прямой, проходящей через эту точку О*. Прямая составляет угол b с ДП объекта. Определим положение точки О*, направление и величину поступательной скорости и угловую скорость поворота объекта вокруг вертикальной оси, проходящей через мгновенный центр О*. Все эти величины легко найти, зная лишь векторы скоростей двух точек объекта.
Спроецируем оба вектора скоростей VК и VН на выбранную прямую и на направление, к ней перпендикулярное. Если указанная прямая составляет с ДП угол b, то проекции будут следующие:
на направление прямой:
VП = VХК cosb + VYК sinb, VП = VХН cosb + VYН sinb, (17)
на направление, перпендикулярное прямой:
VВРК = VХК sinb + VYК cosb, VВРН = VХН sinb + VYН cosb. (18)
Левые части формул (17) одинаковы. Это выражает тот факт, что вдоль искомой прямой направлена единая для объекта его поступательная скорость VП. Следовательно,
VХК cosb + VYК sinb = VХН cosb + VYН sinb,
откуда немедленно следует значение угла дрейфа b
tgb = (VХН – VХК)/(VYН – VYК). (19)
В формулах (18) фигурируют линейные скорости точек К и Н как результат вращения объекта вокруг искомой точки О*. Эти скорости пропорциональны расстояниям LК и LН от центра вращения и поэтому верна пропорция:
LК / LН = VВРК / VВРН = (VХН sinb + VYК cosb)/(VХН sinb + VYН cosb).
Так как угол b уже определен соотношением (19), то возможно найти и отношение LК / LН, т.е. положение центра вращения на ДП, а затем определить и угловую скорость вращения объекта вокруг вертикальной оси, проходящей через найденную точку О*.
w = VВРК / LК = (VХН sinb + VYК cosb) / LК = (VХН sinb + VYН cosb) / LН = VВРН / LН, (20)
где угол b известен из (19).
5. Заключение
Предложенная выше идея и подкрепляющие ее формулы есть основа для введения нового понятия – двухточечной навигации. Она позволит воспринимать судно не как точку, а как объект конечных размеров, и управлять этим объектом, исходя из задачи безопасности мореплавания. Это также открывает возможность в будущем идентифицировать параметры модели управляемости судна, не применяя никаких дополнительных судовых датчиков.
Литература
Абезгауз Г.Г. Справочник по вероятностным расчетам. М., Воениздат, с. 374, 1970.