Заметки о поиске пути
Амит Пател
Перевод с английского: Порицкий А.В.
Источник: Amit’s Notes about Path-Finding, amitp@cs.stanford.edu
http://theory.stanford.edu/~amitp/GameProgramming/
Задача, которую мы пытаемся решить, состоит в том чтобы доставить объект из начальной точки к цели. Поиск пути рассматривается как проблема нахождения хорошего пути от начальной точки до цели обходя препятствия, избегая врагов и с минимумом затрат (топливо, время, расстояние, оборудование, деньги и т.д.). Движение решает проблему получения траектории и движения вдоль нее. Можно потратить ваши усилия только на одно из них. С одной стороны, искушённый первопроходец в сочетании с тривиальным алгоритмом движения найдёт путь, когда объект начнёт двигаться и объект будет идти по этому пути, не обращающая внимание на всё остальное. С другой стороны, система только для движения не будет смотреть в будущее, чтобы найти путь (вместо этого, начальный "путь" будет прямой линией), но вместо того чтобы делать шаг за раз, с учетом местных условий в каждой точке. Лучшие результаты достигаются при использовании поиска пути и алгоритме движения.
ВВЕДЕНИЕ
Движение для единственного объекта выглядит простым. Поиск пути, в свою очередь, носит сложный характер. Зачем нужен поиск пути? Рассмотрим следующую ситуацию:

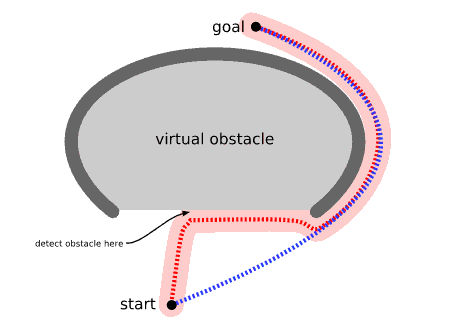
Устройство изначально находится в нижней части карты и хочет добраться до вершины. В области, которую он сканирует (показанно розовым) нет ничего, чтобы указало на то, что устройство не должно двигаться вверх, так что оно по-прежнему следует свому направлению. В верхней части оно обнаруживает препятствия и меняет свое направление. Затем оно находит свой путь вокруг препятствия U-формы, следуя красной дорожке. В отличие от этого, алгоритм поиска пути сканировал бы большую площадь (показанно светло-голубым) и нашел бы более короткий путь (синий), и никогда не посылал бы прибор в препятствие вогнутой формы.
Однако, Вы можете продлить алгоритм движения для обхода ловушки, как показано выше. Либо не создавать вогнутых препятствий или пометить их выпуклые оболочки как опасные (входить только тогда, когда цель находится внутри):
Алгоритмы поиска пути позволяют смотреть вперед и строить планы, а не ждать до последней минуты, когда возникнут проблемы. Существует компромисс между планированием в поиске пути и реагированием в алгоритме движения. Планирование как правило, медленнее, но дает лучшие результаты, движение, как правило, быстрее, но может зайти в тупик. Если игровой мир меняется часто, заблаговременное планирование является менее ценным. Я рекомендую использовать обое: поиск пути для большой картинки, медленного изменения препятствий и длинных путей; и алгоритм движения для локальных областей, быстро меняющегося мира и коротких путей.
Алгоритмы
Алгоритмы поиска пути из учебников информатики работают с графами в математическом смысле - множество вершин с ребрами между ними. Плиточную игровую карту можно считать графом, где каждая ячейка, является вершиной и рёбрами протянутыми между плитками, которые смежны друг с другом:

Сейчас, я буду считать, что мы используем 2х-мерные сетки. Позже, я расскажу, как создать другие виды графов из вашего игрового мира.
Большинство алгоритмов поиска пути от ИИ или алгоритмы исследования предназначены для произвольных графов, а не на основе сетки. Мы хотели бы найти кое-что, что может использовать в своих интересах природу архитектуры карты. Есть некоторые вещи, которые мы считаем общепринятыми, но алгоритмы их не понимают. Например, мы знаем кое-что о направлениях: мы знаем, что в целом, поскольку две вещи становятся более далекими порознь, займет больше времени, чтобы перейти от одного к другому; и мы знаем, что нет никаких секретных червоточин, которые позволяют Вам телепортировать от одного места на карте к другому. (Ну, я предполагаю, что их нет; если есть, становится очень трудно найти оптимальный путь, потому что вы не знаете, где искать в первую очередь.)
Алгоритм Дейкстры и поиск по первому наилучшему совпадению
Алгоритм Дейкстры работает просматривая вершины графа начиная с начальной точки объекта. Затем он циклично проверяет ближайшие, пока еще не рассмотренные вершины, добавляя эти вершины в множество вершин, подлежащих рассмотрению. Он расширяется во все стороны по отношению к отправной точкой, пока не достигнет цели. Алгоритм Дейкстры гарантированно найдёт кратчайший путь от начальной точки к цели, пока ни одино из рёбер не имеет отрицательной стоимости. (Я пишу "кратчайший путь", поскольку часто существует множество эквивалентно коротких путей.) На следующей диаграмме, розовый квадрат является отправной точкой, синий квадрат это цель и синезелёные области показывают какие области алгоритм Дейкстры сканировал. Более светлые синезелёные области это те области, которые находятся дальше от отправной точки, и таким образом формируют "фронт" разведки:

Жадный алгоритм поиска по первому наилучшему совпадению работает таким же образом, кроме того, что он имеет некоторую оценку (так называемую эвристику) о том, как далеки от достижения цели любые вершины. Вместо того, чтобы выбрать вершину ближайшую к исходной точке, он выбирает вершину ближайшую к цели. (Жадных) поиск по первому наилучшему совпадению не гарантирует нахождение кратчайшего пути. Тем не менее, он работает гораздо быстрее, чем алгоритм Дейкстры, поскольку он использует эвристические функции для выбора своего пути к цели. Например, если цель к югу от стартовой позиции, поиск по первому наилучшему совпадению сосредоточен на путях, ведущих на юг. На следующей диаграмме, представлены желтым эти узлы с высокой эвристической оценкой (высокая стоимость, чтобы добраться до цели) и черным узлы с низкой эвристической оценкой (низкая стоимость, чтобы добраться до цели). Это показывает, что поиск по первому наилучшему совпадению может найти путь очень быстро по сравнению с алгоритмом Дейкстры:

Однако оба этих примера иллюстрируют простейший случай, когда ? карте нет никаких препятствий, а также кратчайший путь на самом деле представляет собой прямую линию. Рассмотрим вогнутое препятствие, как описано в предыдущем разделе. Алгоритм Дейкстры работает дольше, но гарантированно найдёт кратчайший путь:

Поиск по первому наилучшему совпадению с другой стороны делает меньше работы, но его путь, безусловно, не так хорош:
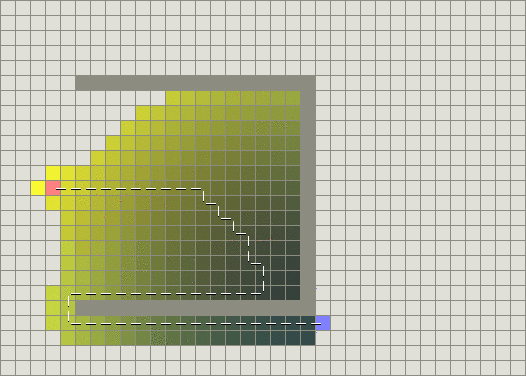
Беда в том, что жадный поиск по первому наилучшему совпадению "жадный" и пытается продвигаться к цели, даже если это не правильный путь. Поскольку это касается только расходов, чтобы добраться до цели и не учитывает затраты на такой далёкий путь, он продолжает идти, даже если путь, по которому он идёт стал на самом деле длинным.
Разве не было бы замечательно взять лучшее от обоих? A* был разработан в 1968 году для объединения эвристического подхода, такого как в поиске по первому наилучшему совпадению и формальный подход, такой как в алгоритме Дейкстры. Это немного необычно тем, что эвристические подходы как правило, дают вам примерный путь к решению проблем, без гарантий того, что вы получите лучший ответ. Тем не менее, хотя A* и построен на основе эвристики, и сама эвристика не дает гарантии, A* может гарантировать нахождение кратчайшего пути.
Алгоритм А*
Я буду фокусироваться на алгоритме A*. A* является самым популярным выбором для поиска пути, потому что он достаточно гибкий и может быть использован в самых различных контекстах.
A*, как и другие граф-алгоритмы поиска, потенциально может искать на огромной территорию карты. Он как алгоритм Дейкстры в том, что может быть использован для поиска кратчайшего пути. Он как жадный поиск по первому наилучшему совпадению в том, что он может использовать эвристику для направления себя. В простом случае, он так же быстр, как поиск по первому наилучшему совпадению:

В примере с вогнутым препятствием, A* находит путь так же хорошо как и алгоритм Дейкстры:

Секрет его успеха в том, что он сочетает в себе фрагменты информации, которые использует Алгоритм Дейкстры (предпочитаемые вершины, которые близки к исходной точке) и информацию, которую использует поиск по первому наилучшему совпадению (предпочитаемые вершины, которые близки к цели). В стандартной терминологии, используемой когда речь идет о A*, g(n) представляет собой стоимость пути от начальной точки до любой вершины n, и h(n) представляет собой эвристическую полную стоимость от вершины n к цели. В приведенной выше диаграммы, желтым (h) представлены вершины далёкие от достижения цели, а синезелёным (g) представлены вершины далёкие от начальной точки. A* балансируя между обоими движется от начальной точки до цели. Каждый раз в основном цикле в нем рассматриваются вершину n, на предмет самого меньшего значения f(n) = g(n) + h(n).